LSSL

LSSL : Abstract

• Linear State Space Layer : mapps a sequence by simulating a linear cont-time state space representation
• Theroetic : LSSL = RNN, NDE, Temp. convolution과 모두 관련이 있음
• generalize A matrix for cont. time memorization

Intro

• RNN = natural stateful model : constant computation and storage per t. but slow train + opt. difficulties (Vanishing gradient)
• CNN = local context, parallelizable train b. not sequential → expensive inference, context lenght limitation
• NDE = matehmatical, theroetically addressable, but inefficient

⇒ combinational benefits of parallelizable training, stateful inference, time scale adaptation!

• 이러한 장점들을 모두 가지기 위한 여러 모델들이 등장했으나 여전히 reduced expressivity problem 존재 → 보다 expressive한 모델을 만들자
  
• Linear State Space Layer : maps 1 dimensional function or sequence through an implicit state
  • A : controls evolution of the system
  • B, C, D : projection parameters
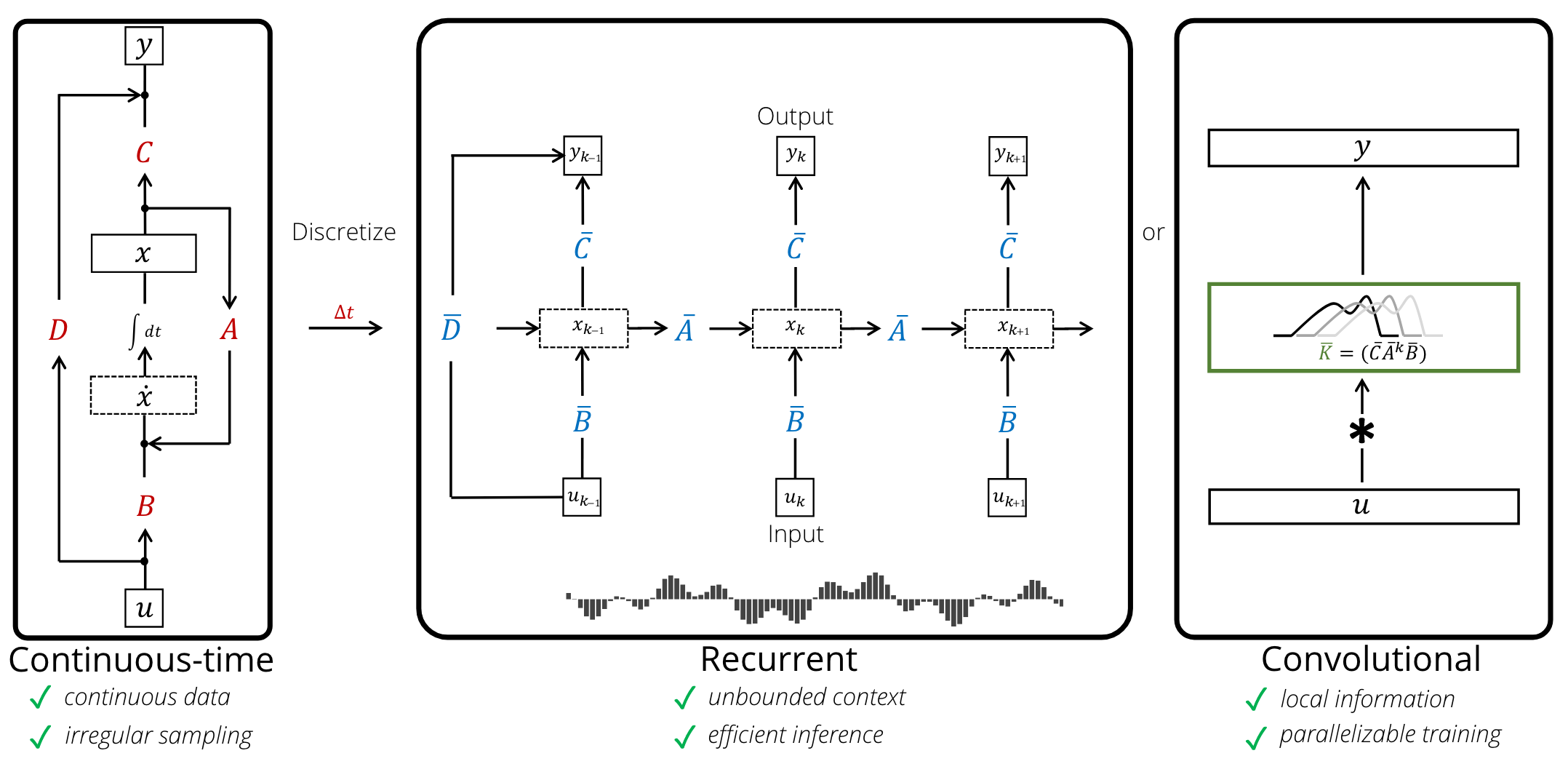
  • LSSL = instantiation of each family
  • recurrent : discrete step size specified → discretized into a linear recurrence
  • convolutional : continuous convolution수식이라고 볼 수 있으며 discretize될 경우엔 병렬 계산도 가능함
  • cont-time : differential equation → continuous 하게 작업이 가능함
  • 또한 express-able : generalize CNN and RNN
    1. control theory - 1-D conv.kernels can be approximated by an LSSL
    2. RNN = ODE (gate mechanism) related and derived from ODE approx → LSSL = special case
  • generality = tradeoff
    • limitation of RNN and CNN is inherited
    • state matix A and time scale is very critical and computationally infeasible
    • 어떤 행렬을 골라야하는지를 골라둘 것임

Technical Background

• Approximation of diff. eq
  • $x(t) = x(t_0) + \int_{t_0}^t f(s, x(s))ds$
  • finds a sequence of functions x0(t), x1(t), . . . that approximate the solution x(t) of the integral equation.
• Discretization
  • generalized bilinear transform for linear ODE
    
  • alpha = 0 : Euler, 1 : backward-Euler, 1/2 : bilinear (stability preserving)
• $\Delta t$ as Time scale
  • 대부분의 경우 length of dependencies 에 반비례함 → timescale이라고 볼 수 있음 = ODE-RNN들의 기조
• Cont-time memory
  • HIPPO 참조 : exponential -growing continuous time memory

LSSL : Linear State-Space Layers

• As a recurrence : t-1 시점의 x가 앞선 정보를 모두 가지고 있다고 생각하면 recurrent한 모델으로 정의가 가능함. y는 최종 결과물임. 고정된 computation과 storage로 계산이 가능함
• As a convolution : initial state - 0 이라고 하면 앞선 수식을 커널 연산으로 정의할 수 있음
  • 최종적으로는 푸리에 연산으로 한번에 계산이 가능함
• 병목현상 = 행렬벡터 계산과 krylov function으로 해결할 수 있음 (캐싱해두고 가져와서 쓸 수 있음 )
  • 물론 이걸 구하는거 자체가 문제가 될 수 있음..

Expressivity of LSSLs

• Convolutions are LSSLs
  • output y = convolution of input u (h = impulse response)
  • arbitrary convolutional filter h = approximated by a rational function and represented by an LSSL
  • Hippo matrix를 가진 경우에는 고정된 dt에 대해서 윈도우 사이즈만큼에서의 특징을 뽑아내는 것임
• RNNs are LSSLs

  • gating mechanism of RNN = smooth optimization = analog of a step size!

    

  • each layer = Picard iteration → can be approximated by ODE

Deep LSSL

• seq2seq of parameters with size N
• hidden dim H에 대해서 각 parameter broadcast(independent)

Combining LSSLs with Continuous-time Memorization

Incorporating Long Dependencies into LSSLs

• Hippo = how to memorize a function in continuous time w.r.t a measure $\omega$
• Optimal memorization operator hippo(w) has form x(t) = A(x(t) + Bu(t), A = low recurrence=width state matrix

Theoretically Efficient Algorithms for the LSSL