MAMBA-2: SSD Part 2 - The Theory
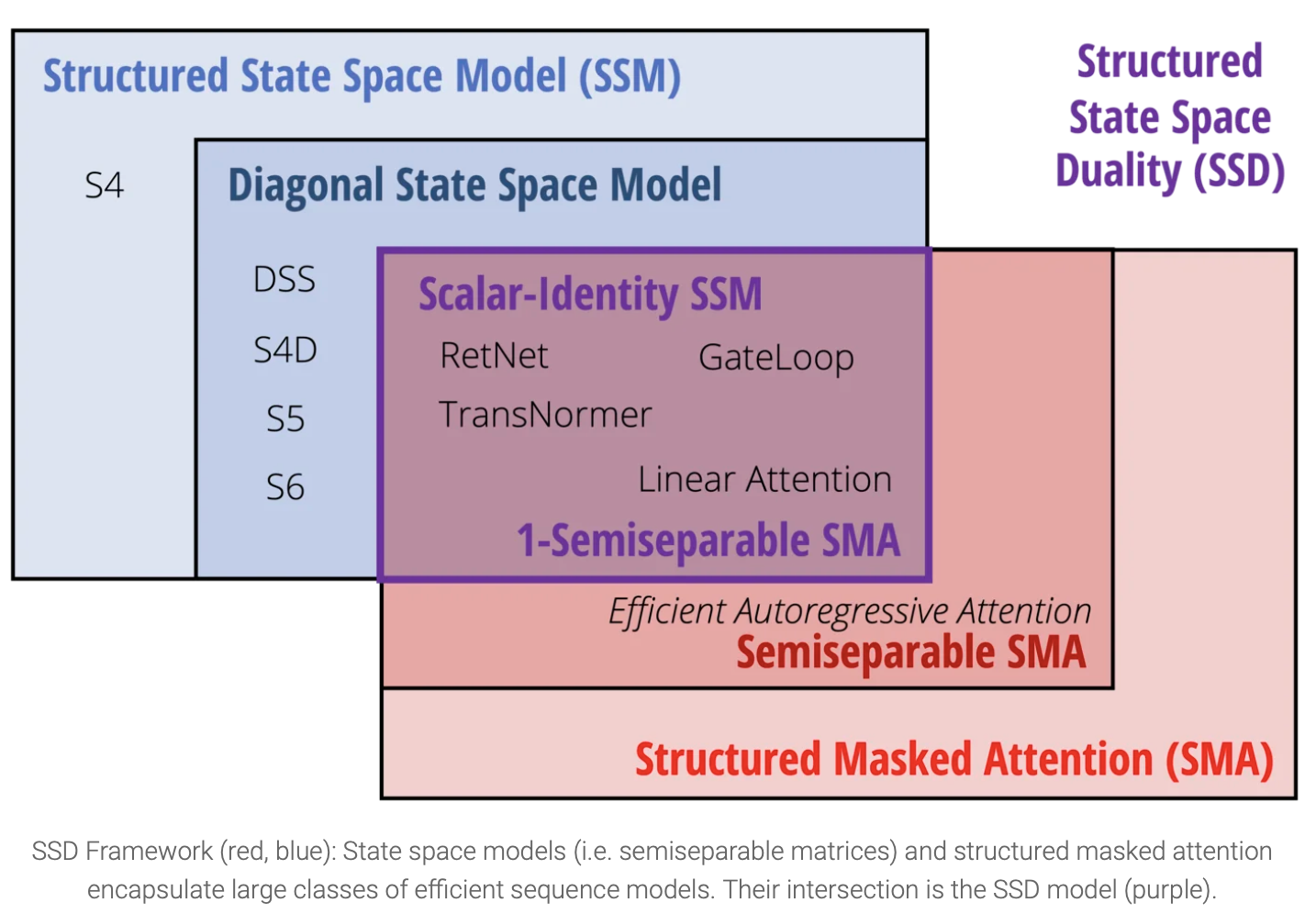
State Space Duality
- 첫번째 포스트에서는 SSD 가 모델에 어떻게 적용되었는지를 살펴보았다면, 이번에는 SSD duality를 SSM과 attention 측면에서 각각 살펴볼 것이다.
- 두 방법 모두 기존 모델보다 폭넓은 적용 가능성을 가지며, 이것이 SSD framework를 완성한다.
- Define the general concepts
- Show how the SSD model is an instantiation and prove the duality
- Suggest future directions for how the framework can be used
Recap : The SSD Model
- SSD layer : scalar identity structure on A
ht=Atht−1+Btxtyt=CtTht
- sequence transformation으로도 생각해볼 수 있고, dual attention form으로도 작성할 수 있다.
Y(T,P)=SSM(A(T,...).B(T,N),C(T,N)(X(T,P))
M=L∘CBT∈R(T,T)
- 핵심 아이디어는 여러 시퀀스 모델들이 X를 Y 로 매핑하는 matrix multiplication으로 표현이 가능하다는 점에서 출발한다.
- 이러한 관점은 “sequence mixer” or “token mixer”로도 불리며 matrix sequence transformation 은 matrix mixer라고 할 수 있다. 가장 잘 알려진 예시로는 self-attention에서의 attention matrix를 들 수 있겠다.
- 이렇게 행렬식으로 나타내면 시퀀스 모델의 특징과 구조를 더 잘 알 수 있다.
- 일반적인 RNN이나 LSTM은 matrix mixer로 작성이 어렵지만, SSM은 작성이 가능하다. SSM의 recurrence를 다시 쓰기만 해도 증명이 가능하다.
Y=SSM(A,B,C)(X)=MX
Mij=CiTAi,j×Bj:=CiTAi...Aj+1Bj
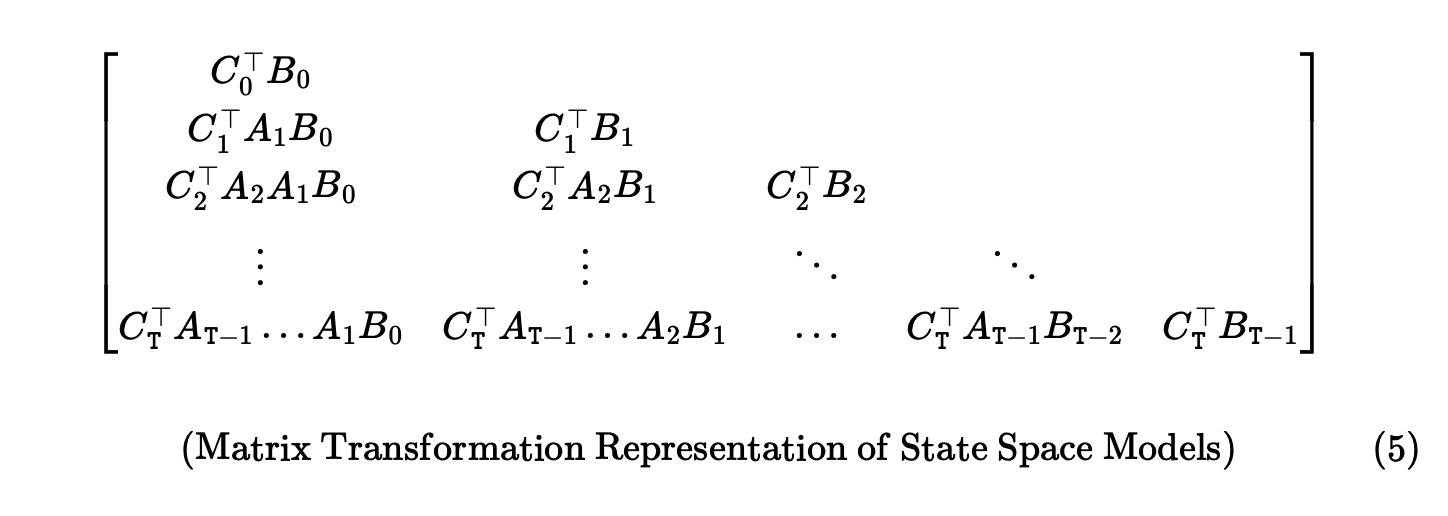
Semiseparable matrices

- 이런 형태의 행렬을 semiseparable matrix라고 불린다. 여러 유용한 특성을 가지는데 그중 하나가 structured rank property라고 불리는 lower triangle 에 속하는 모든 부분 행렬이 low rank라는 특징을 가진다.
- 알고리즘 측면에서 이를 접근하면, 이런 행렬이 우리의 목표인 보다 간단하게 matrix multiplicaton algorithm으로 계산이 가능하게하는데 적합하다는 걸 알 수 있다.
Deriving the Duality: SSM to Attention
- scalar identity structure을 가지는 SSM에 대해서, 행렬을 보다 간단하게 작성할 수 있다.
CiTAi:j×Bj=Ai:j×⋅(CiTBj)
- 결론적으로, SSD model의 duality는 2개의 semiseparable matrix에 대해 서로 다른 matrix multiplication algorithm을 적용한 것과 같다.
- linear form은 structured matrix multiplication algorithm으로 sequential하게 행렬곱을 하게 되고 quadratic form은 기본 matrix multiplication으로 full matrix를 만들게 된다.
Algorithms
- 알고리즘 측면에서 이러한 duality result, asymptotic efficientcy result, more general hybrid algorithm을 제안한다.
- block decomposition of the semiseparable matrix를 통해 계산을 가능케한다.
Understanding
- Sequence model에 대한 시각을 통합해서 볼 수 있게 된다.
- New sequence model : 새로운 sequence model을 찾는 것이 target property를 가지는 특정한 structured matrix를 찾는 과정으로 해석될 수 있다. 이는 Bidirectional Mamba로 곧 찾아올것…….← 어떡해..
- Expressivity: matrix transformation을 살펴보면 linear algebraic하게 해석할 수 있음을 알 수 있고 subquadratic model 연구에 적용이 가능하다.
- Interpretability : Mamba model의 내부 정보에 대해 알 수 있다.
SSD Framework 2: Structured Attention
- 두번째 뷰는 어텐션 측면에서의 해석이다. Tensor contraction을 통해 이를 해석할 수 있다.
- Attention 역시, 행렬 mapping으로 작성할 수 있다.
(Q(T,N),K(S,N),V(S.P)↦Y(T,P)
- Attention score는 Q, K의 커널 매핑의 곱으로 표현할 수 있고, 여기서는 kernel 이 finite 한 경우로 한정한다.
Y=Q⋅(KTV)
- 이렇게 정의하게 되면 sequence 길이가 길어지고 channel 수가 작아지면 attention이 quadratic complexity에서 linear complexity로 복잡도가 줄어들 수 있기 때문이다. 이렇게 되면 행렬곱을 다른 순서로 진행하는 것과 같아진다. 행렬곱의 assosicativity로 해석할 수 있는 것이다.
(Causal) Linear Attention
- 그러나 basic kernel attention이 약간 변형되면 이런 matrix multiplication associativity를 바로 적용할 수 없다.
- 그럼에도 Linear Attention은 attention에 causality를 적용하며 사용될 수 있음을 보일 수 있다.
- The quadratic form of causal linear attention은 아래와 같이 정의할 수 있고 여기서 L은 causal mask matrix이다.
Y=(L∘QKT)⋅VL=⎣⎢⎢⎢⎢⎡11⋮11⋯1⎦⎥⎥⎥⎥⎤
- 여기서 문제는 L을 적용했을 때, 행렬간 교환법칙을 적용할 수 없다는 것이다. original linear Attention paper는 이것을 피하고자 다른 방식으로 quadratic attention을 해결하려한다. 이 글에서는 복잡한 증명은 두고, 이것이 어떻게 선형성을 보장하는지에 대해 살펴보자.
Y=Q⋅cumsum(KTV)
- 사실 L은 matrix multiplication에서 cumsum을 인코딩한 결과이다!
A Tensor Contraction Proof of Linear Attention
- einsum notation을 이용해 이러한 linear attention을 정리하면 shape annotation으로 작성할 수 있다.

- 이를 보면 자연히 L이 cumsum임을 이해할 수 있다.
Structured Masked Attention
- 이런 연산이 빠르게 진행되려면 L은 structured matrix 여야 한다. 즉, subquadratic matrix-vector 연산이 가능한 행렬이어야 한다.
- 여기서 SMA 는 위의 equation 8 을 의미한다. SMA는 dual quadratic 과 linear mode 를 가진다.
- matrix multiplication의 associativity는 결국 tensor contraction reduction order의 한 종류이므로 바로 적용이 가능한 것이다.
Deriving the Duality: Attention to SSM
- SSD은 scalar-identity SSM이나 Attention like equation 두가지로 적을 수 있다. 두 형태의 동일성을 보이고자, 앞서 정의했던 M이 structured masked attention이 아래의 L과 같은 특별한 케이스임을 기억하자.

- 이 행렬을 1-semiseparable matrix라고 부른다. 즉 SSD model도 1-semiseparable masked attention이라고 볼 수 있다는 것이다.
- 직접 적어보면 결국 y = Lx가 scalar recurrence로 귀결되는것을 확인할 수 있으며 이것이 결국 SSM recurrence이다.
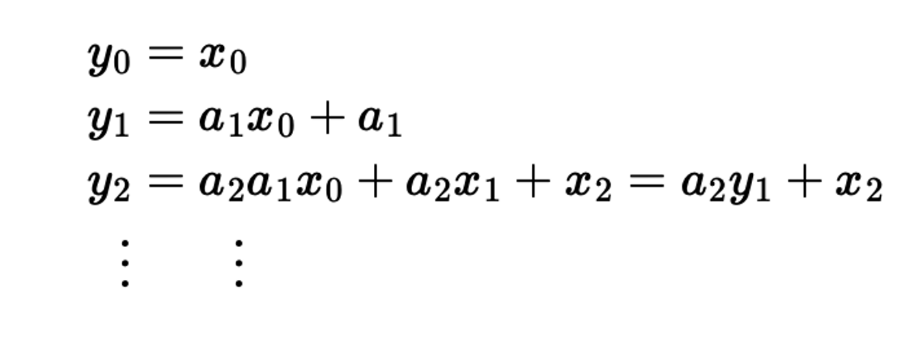
Going beyond the SSD Layer 2
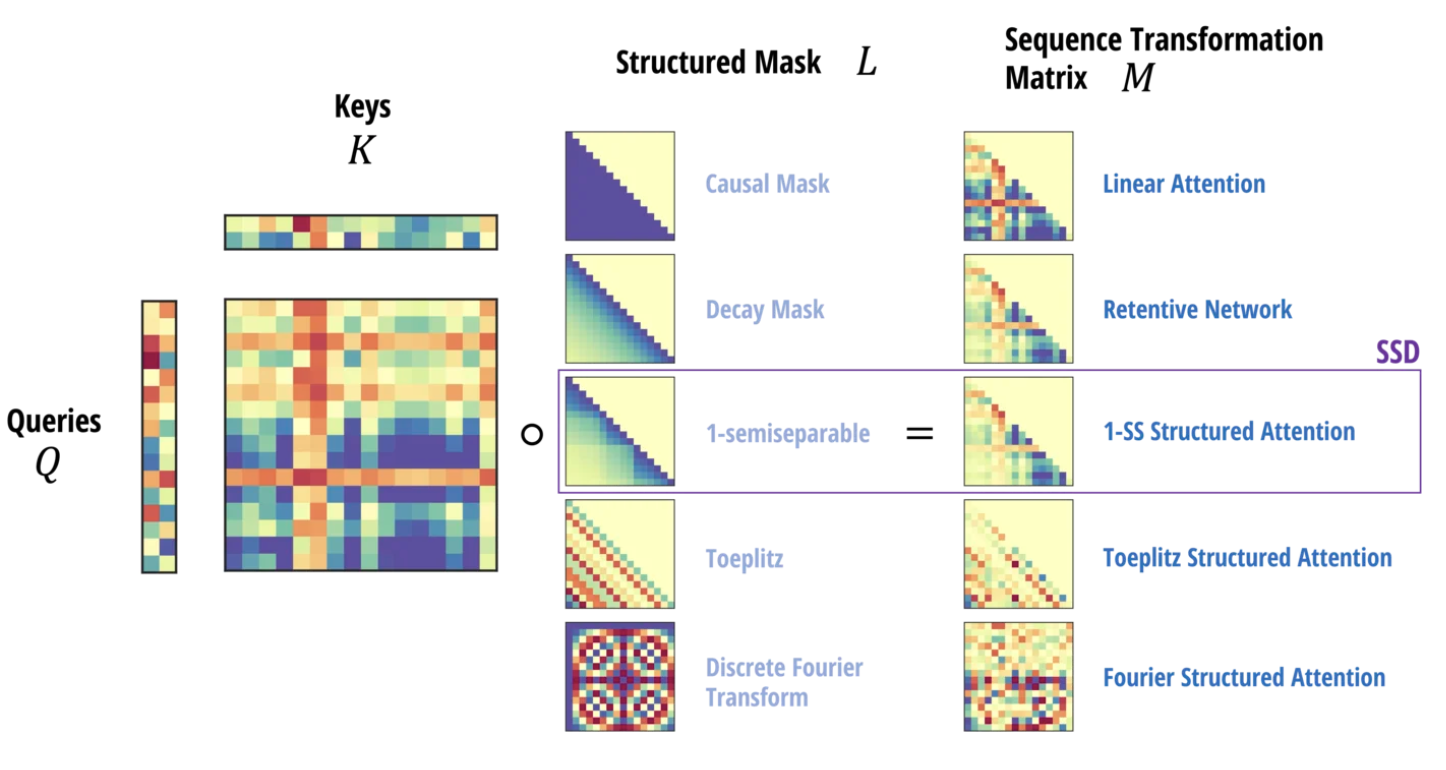
State Space Duality Summarized
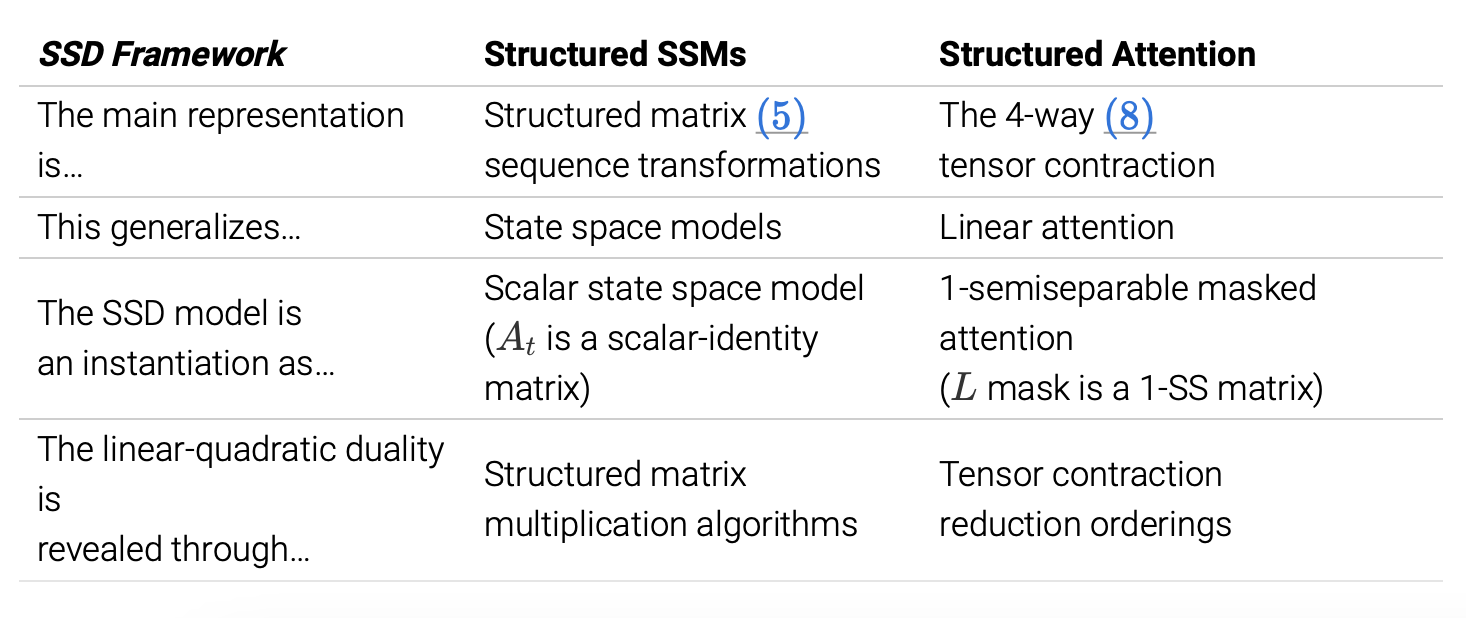





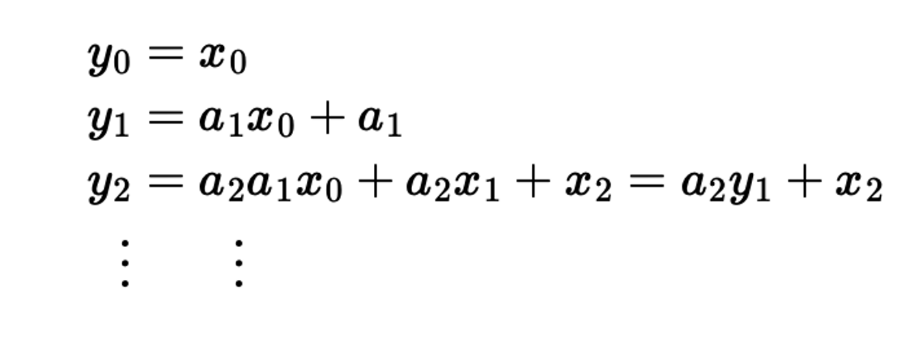



Bidirectional Mamba로 곧 찾아올것…….← 어떡해.. ㅋㅋㅋㅋㅋ