Source State Space Duality
Part 1: The model
- MAMBA도 좋은 성능을 보였지만 여전히 문제가 있었다.
- 문제 1: 이해하기 어려움
-
Mamba는 SSM을 활용하여 sequence modeling의 많은 부분을 address할 수 있었지만, attention mechanism과 유리된 부분이 있다고 생각된다.
→ SSM과 Attention간의 이론적 연관성이 무엇일까? 둘을 혼합할 수 있을까?
-
- 문제 2: 효율성
-
HW-aware algorithm은 여전히 attention보다 계산적으로 효율적이지 못하다.
-
현대 GPU, TPU는 행렬 연산에 최적화되어 있으며 Training period에서의 계산 개선도 필요하다.
→ Mamba to matrix multiplication이 가능할까?
-
The SSD Model
- SSD model : a layer like attention or an SSM
- SSD framework : general framework for reasoning about this model
- SSD algorithm : SSD layer 계산을 보다 효율적으로 하기 위한 알고리즘
The Linear (SSM) mode
- SSM 은 인 매핑이다.
- selective SSM은 (A, B, C)가 시간에 따라 달라질 수 있도록 한다.
- Structured SSM은 보다 효율적인 계산을 위해 A 가 대각행렬이 되도록 한다.
- S6도 그렇다.
- SSD는 약간의 변형을 거친다. A가 대각행렬일 뿐만아니라, scalar times identity structure임을 필요로한다.
- 즉, A의 대각원소가 모두 같은 값이 되도록 한다. 따라서 단순히 A를 shape과 scalar로 표현이 가능하다.
Multihead SSMs
- 기본 SSM 수식은 single dimension에 대해 정의된다. 만약에 P개의 채널을 가진다면, 각 채널에 독립적으로 같은 행렬을 적용하는 것이다. 이것은 single head SSM이다.
- 여기서 X가 (T, P)인 텐서라면, P에 대해 multiple head를 적용할 수 있다. 각각 독립적으로 만들면 되므로 설명은 single에 대해서 한다. (multihead attention과 유사하다)
- 따라서 보다 general하게 SSM을 다시 쓰면
- 여기서 A의 모양에 따라 아래와 같이 달라진다.
- (N, N) : general
- (N) : diagonal
- () : scalar ← SSD
- input output개수 등에 대해 더 많은 변형이 가능하지만 일단 Mamba 1에 집중한다.
The Quadratic (Attention) Model
- 잠시 SSM에서 빠져나와서,

- 이러한 행렬이 있다고 하자.
- 여기서 아래와 같은 행렬을 정의하자. 이렇게 정의하면 M은 sequence transformation을 기본적인 행렬 연산을 통해 수행할 수 있다!
- 이는 attention과 굉장히 유사하며, 만약 모든 이라면, 단순한 lower triangular causal mask 이며, 이는 곧 causal linear attention이다.
→ SSM의 행렬들과 attention 간의 연결고리
State Space Duality
- 앞서 정의한 scalar-identity sturcuted A case의 SSM 과 지금의 M행렬은 사실 같은 모델이고, 그 모델은 아래와 같이 정의할 수 있다.
- 결국 어떠한 행렬들의 선형변환이다..?
SSD vs. State Space Models
- 결국 mamba 1에서 바뀐점
- diagonal A → scalar-times-identity structure A
- recurrent dynamic을 전체 state space의 원소들과 공유
- P = 1 (channel) → P > 1
- P heads를 통해 channel들에도 공유
- diagonal A → scalar-times-identity structure A
- 결국 P x N 만큼 개별적으로 scalar recurrence를 말하던 mamba 1에서 single shared recurrence를 말하는 mamba 2가 된다.
- 이는 모두 계산 효율성을 위한 것으로 dual (quadratic) attention form으로 모델을 해석할 수 있게 되어 행렬연산이 가능하다.
- 성능에 문제가 있을지 걱정될 수 있지만, selectivity때문에 무시해야할 것은 전체에서 무시하고 가져갈 건 전체에서 가져가니까 괜찮다. 물론 아직 실험적으로만 증명되었고 이론적인 증명이없어서, 학습시간에는 mamba2가 나아도 mamba1이 추론 시 정확도가 더 높을 수도 있다.
SSD vs. Attention
- 트랜스포머와 다른점
-
softmax-norm을 제거
- 효과적인 state size를 한 scale 줄임 (선형→상수, quad→ linear)
-
separate element-wise mask matrix를 multiplicative하게 적용
b. 독립적인 Positional encoding이 가능해진다. 마스크 L의 weight에 따라서
- 이는 discount factor로 해석 가능하며 input의 영향을 고려하는 마스크로, mamba의 selectivity를 encode할 수 있다.
Best of Both Worlds
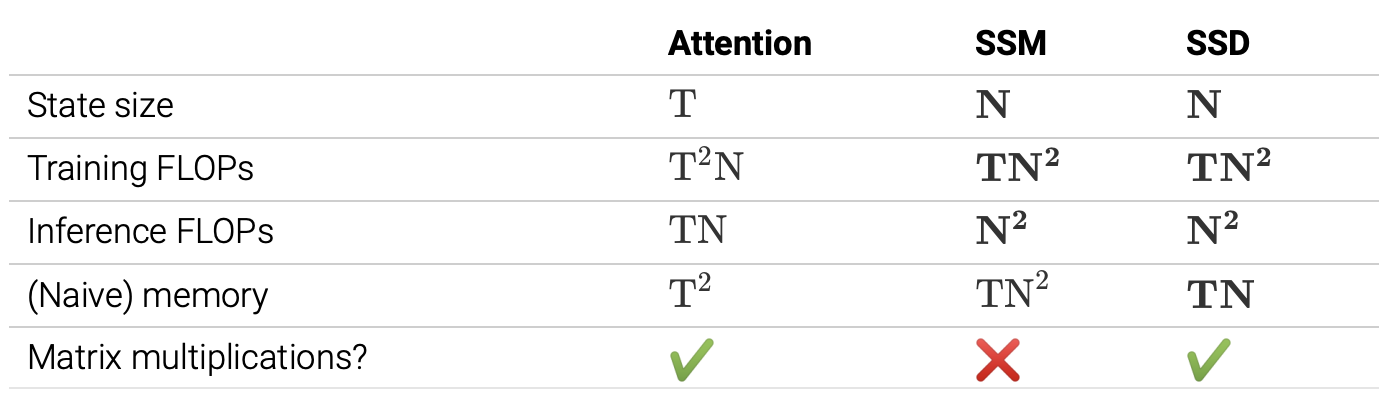
Efficiency: the SSM and Attention Modes
- SSM and attention은 같은 함수를 계산하는 다른 방법이다.
- SSM은 recurrence를 이용하여 constant size, linear scale factor를 가진다는 장점이 있다. 그러나 실제 FLOP을 생각해보면 좀 느려지는 경향성이 있다.
- 반면, sequence transformation을 계산하려면 quadratic time이 걸리게 되는데, 실제로는 GPU, TPU 연산을 통해 빠른 행렬연산으로 수행이 가능하다.
Efficiency: the SSD Mode
- 그렇다면 언제 어떤 모드를 사용해야할까?
- inference 시에는 trade-off 가 없이 SSM을 사용하면 좋다. 그러나 trainiing 때에는 계산 시간과 하드웨어 효율성을 생각해야하므로 matrix multiplication을 통해 계산하는게 바람직하다.
- 따라서 SSD를 이용한 SSD algorithm을 이용하면 효율적으로 계산이 가능하다.
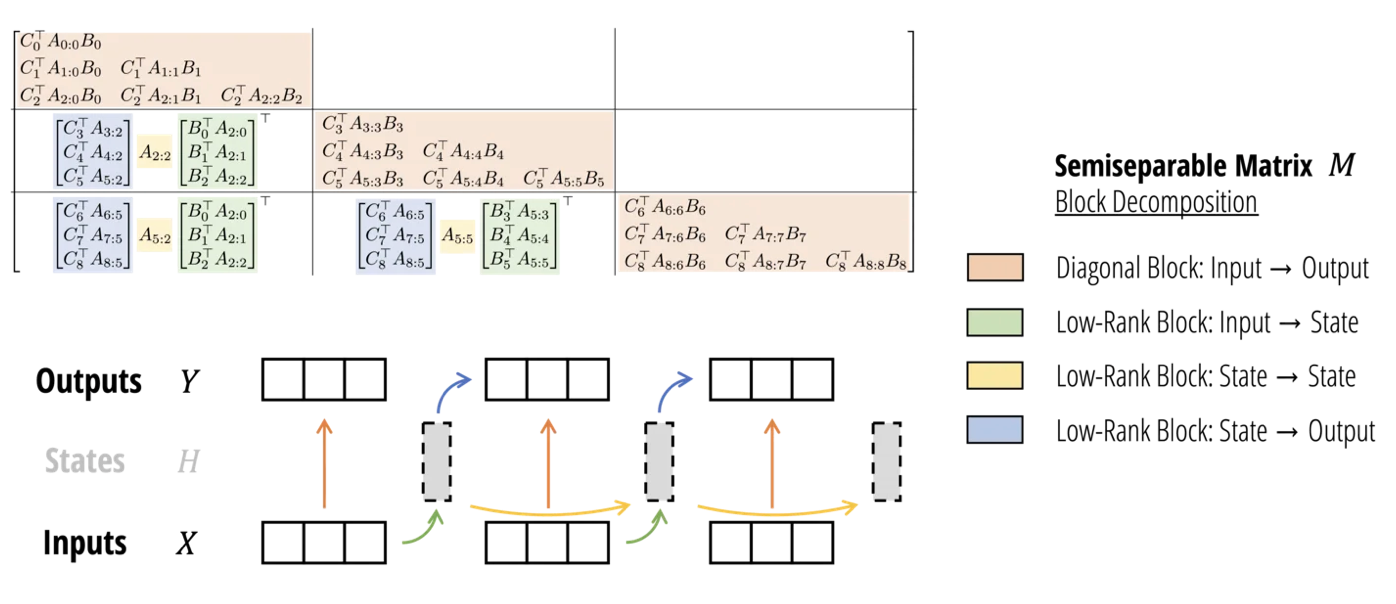
- block decomposition of a particular structured matrix that defines the SSD “token mixing” sequence transformation.
- SSD의 sequence transformation을 정의하기 위한 분해가 필요
- chunkwise algorithm that splits the sequence into segments, compute quad-attention on each element, and adjust the result by passing the SSM states btw segments
- 세그먼트 단위로 잘라서 각각에 대해 attention을 수행한 뒤 SSM state의 결과를 반영하는 것.
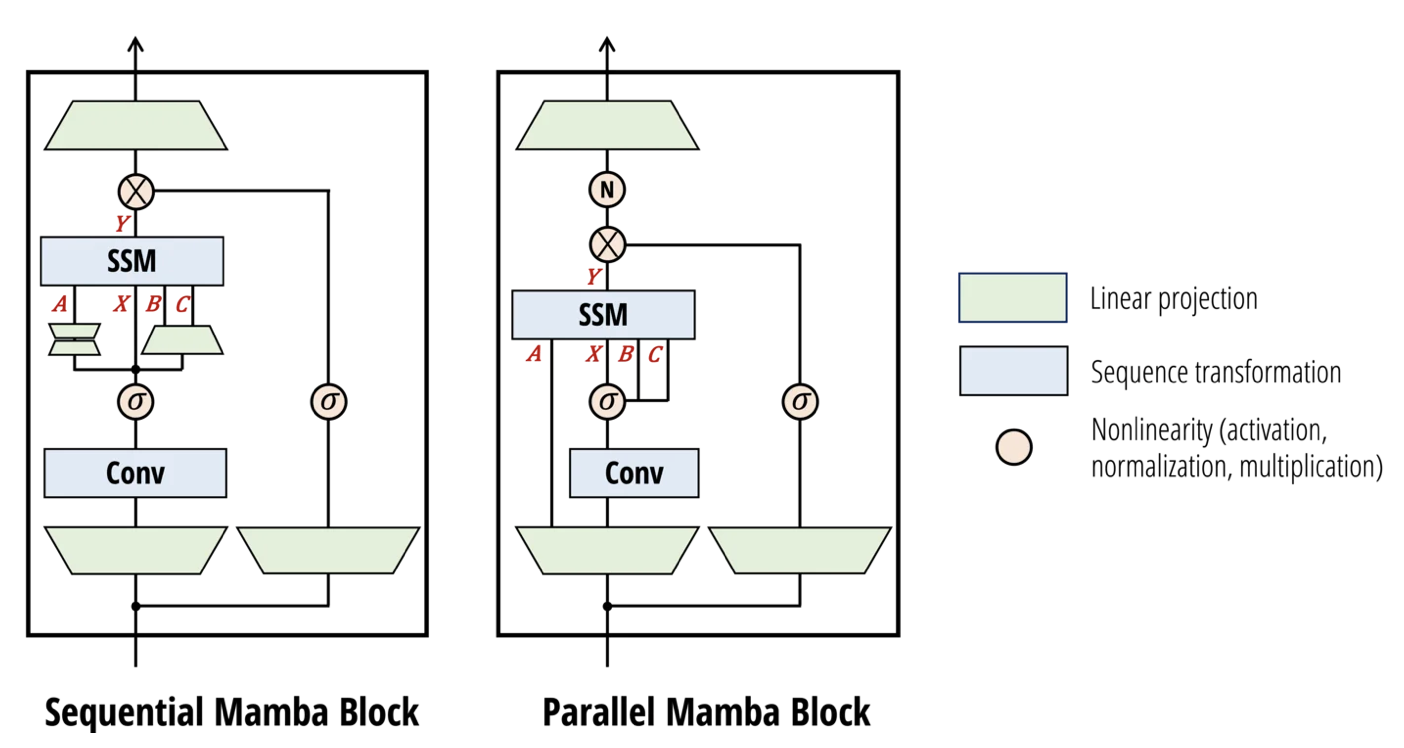
The Mamba-2 Architecture
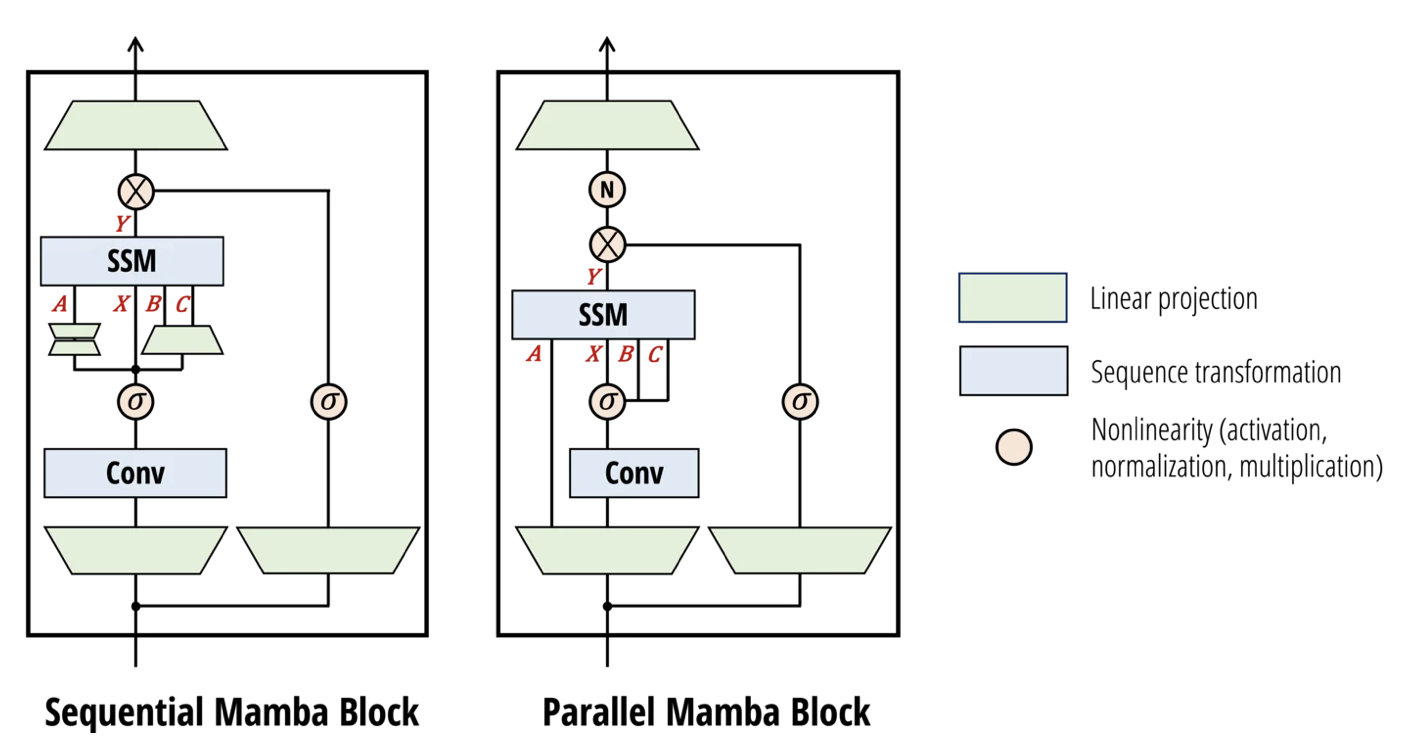
- 기존 mamba에 약간의 변형을 거침
- A, B, C와 X를 병렬적으로 처리 (sequential하게 처리하는 대신에)하는 것으로 변경하였다. 이는 attention과의 연결성 뿐만아니라 tensor parallelism을 적용하기 위함이다.
- 추가적인 변형은 논문을 참고하라.
Language modeling
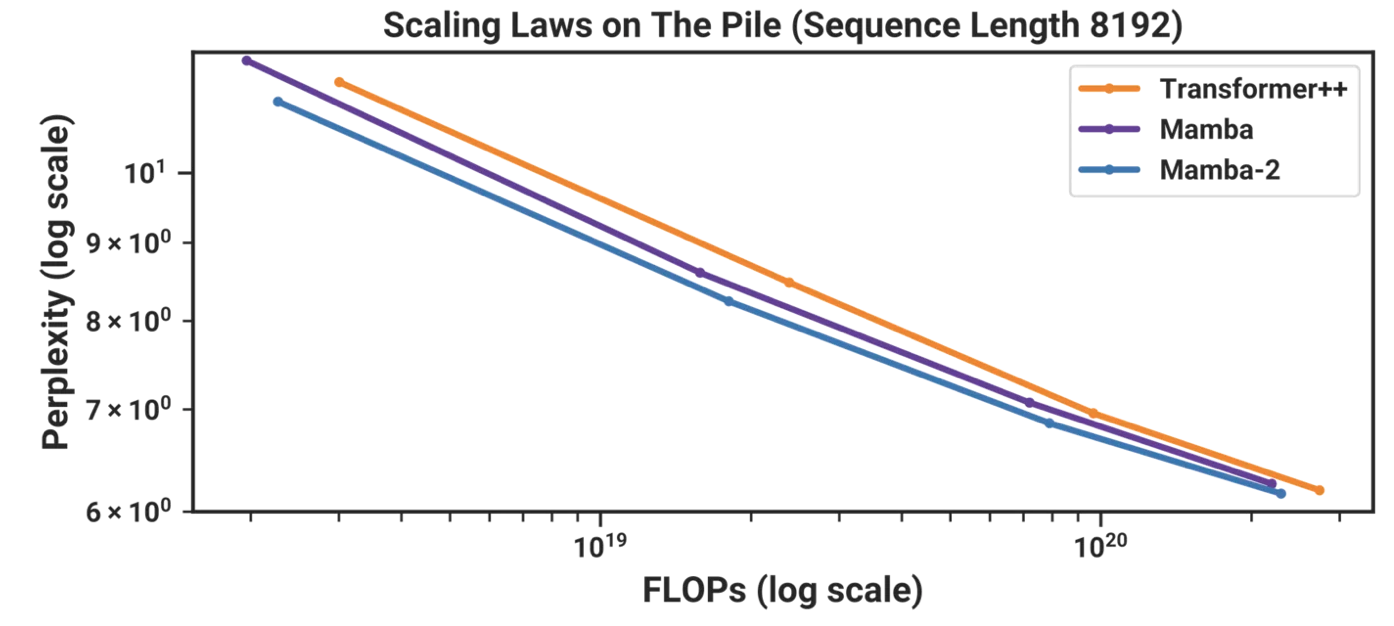
- Pile dataset에 대해 test 한 결과이다.
Synthetic Language Modeling : MQAR
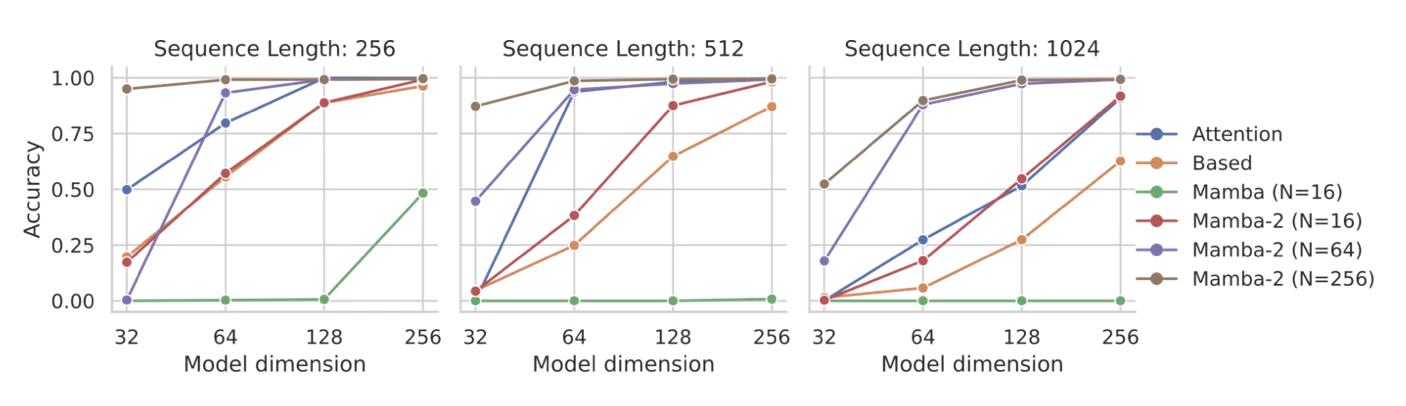
- Multi-Query associative recall
- mamba-1보다 mamba-2가 전체적으로 더 좋은 성능을 보였다.
- 정말 SSD가 효과적인걸까? ← 추가적인 ablation study가 필요하다.
