[논문리뷰] Representation Degeneration problem in Training Natural Language Generation Models
Language Modeling
목록 보기
1/6
Paper link(ICLR 2019)
Intro
- 워드 임베딩은 모델의 첫번째 레이어로 softmax parameter과 연결되어 있기에, first layer의 input이자 마지막 layer의 weight로 기능한다. 따라서 임베딩은
- 언어의 문맥을 담아야하면서도
- classifier로서의 기능을 할 수 있어야 한다.
- 그러나 vaniila transformer의 임베딩을 SVD를 통해 시각화해보면, narrow cone 모양으로 나타나며, 어떤 두 단어를 골라도 모두 positive correlation을 가지는 것으로 나타났다. 즉, 제대로 문맥을 배우지 못한 representation degeneration problem이 발생한 것이다.
- 이 논문에서는 representation degeneration 문제에 대한 직관적인 설명과 이론적 증명을 진행한다.
- 직관적으로, 학습 과정에서 negative log likelihood loss 등으로 학습을 진행할 때 , 정답 단어는 hidden state방향으로, 다른 단어들은 그 반대방향으로 학습이 진행될 것이다. 비슷할수록 더 큰 유사도를 가지고, 다를 수록 작은 유사도를 가지도록 학습하는 것이다. 그러나 언어 corpus는 매우 방대하고, 따라서 하나의 정답단어 방향보다 나머지 단어들의 반대방향이 훨씬 커질수밖에 없다. 결국엔 한 방향으로 몰리도록 학습되는 것이다. 이를 확인하고자 non-appeared word에 대한 embedding이 어떻게 생성된 것인지 보여준다. 저자들은 이런 문제를 해결하기 위해서 regularization term을 설계한다.
Experiments & Understanding the problem
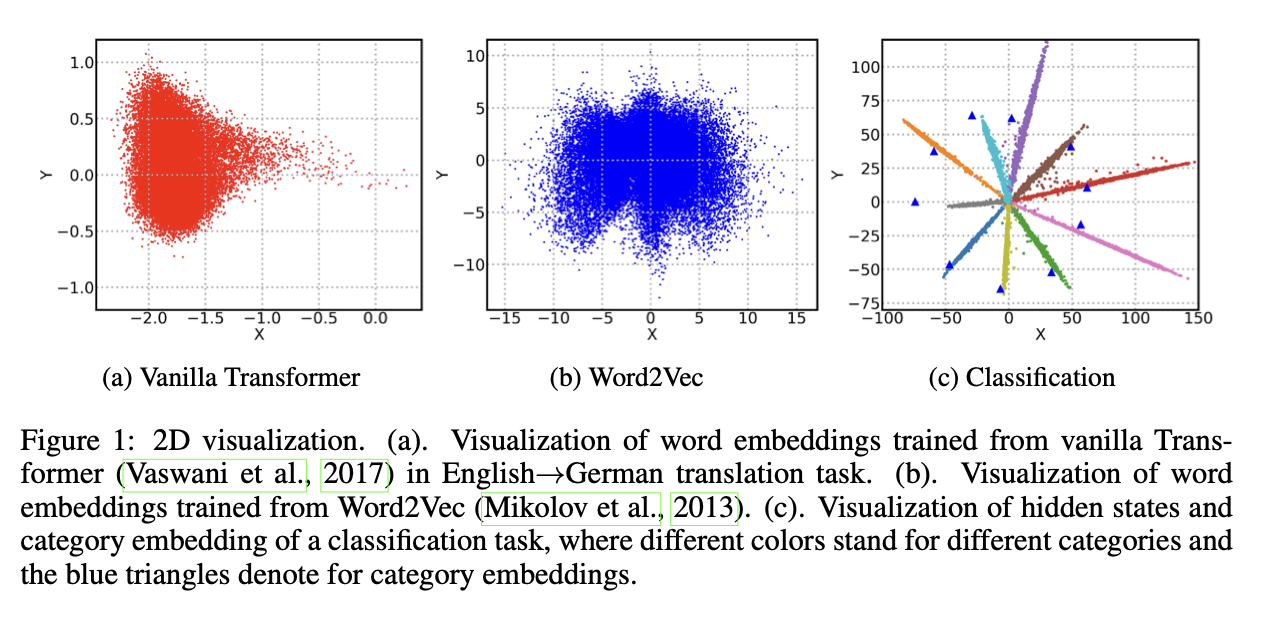
- weight matrix from conventional word representation learning과 softmax layer of classification task와 임베딩을 비교한다. 또한, SVD로 2D plot과 singular value plot을 보여주며 low rank approximation 이 reasonable 한지 체크한다.
- 위 플롯을 확인해보면 machine translation에서의 임베딩이 기존 train된 임베딩과는 달리 한쪽으로 치우친 분포를 가지는 것을 확인할 수 있다.
Extreme case: non-appeared word token
-
만약, 학습동안 등장하지 않은 단어가 들어왔다고 생각해보자. 이는 extreme low frequency word라고 할 수 있다. 학습과정에서 다른 파라미터들은 모두 잘 학습되었다고 가정할 때, 우리는 아래 최적화과정을 진행하게 된다.
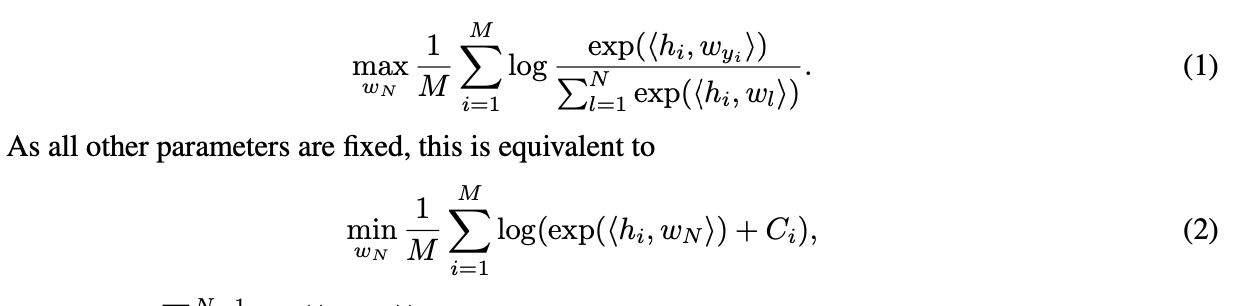
-
그리고 theorem 1에 의해 이 희소단어는 unbound하게 된다. 즉, 어떠한 Uniformly negative direction(어떤 토큰과의 내적이 모두 0보다 작음)이 존재한다면, 이 단어는 어떤 방향으로든 무한대로 최적화될 수 있다는 것이다. 여기서 uniformly negative direction은 convex set이므로, w_N은 convex cone에 위치하게 되며 Infinite로 발산할 것이다.
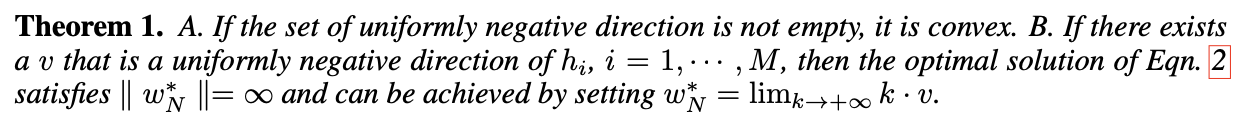
-
Theorem 2는 여기에 더해 uniformly negative direction이 존재함을 보인다. 여기서 우리는 이 조건이 성립하는 것은 hidden state 의 구조에 의존한다는 것을 확인할 수 있다.
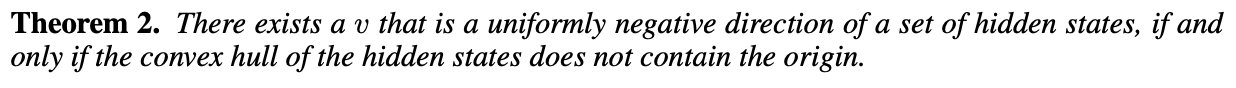
Extension to rarely appeared word tokens
- 보다 현실적인 가정 하에서 다시 생각해보자. 여기서 생각해봐야할 것은 거의 등장하지 않았던 word token이 아예 등장하지 않은 토큰과 유사하게 작동하는지를 확인해보면 된다. 똑같은 수식에서, optimization이 어떻게 수행될 지 생각해보자.
- Loss를 2개로 분해해서 희소 단어를 포함한 문장과 그렇지 않은 문장에 대한 loss가 있다고 하자. 그러면 희소단어를 포함하지 않은 에 대해서 은 non-appeared라고 볼 수 있고, 결국 아래와 같은 식으로 정리할 수 있다. 여기서의 은 convex하다.
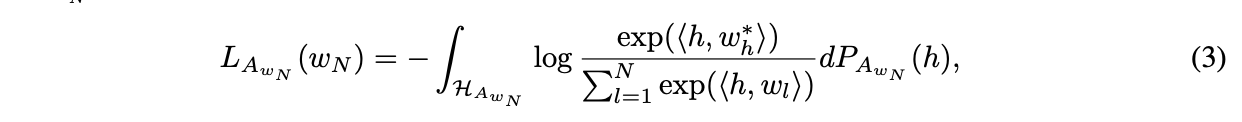
- 희소단어를 포함한 은 문장에서 을 기반하여 계산이 가능하고, (즉 의 next token prediction) 따라서 아래처럼 loss를 계산한다. (사실상 수식은 똑같은데 계산 공간이 다름.) 에 따라 계산되기에, non-convex이다.
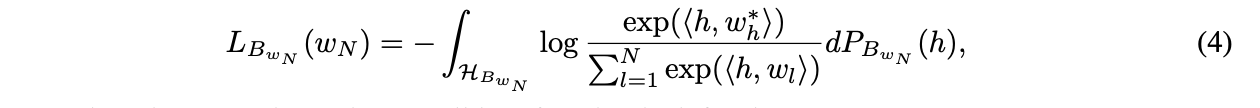
- 최종 loss는 두 loss의 합으로 정의된다. 만약 이 매우 크다면, 은 bounded-smooth function이 될 것이고, 만약 이 strongly convex하다면 unique solution을 가진다.
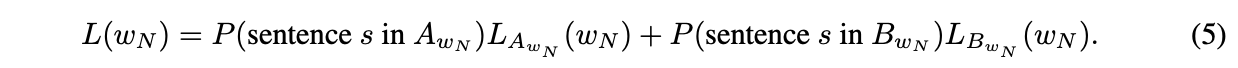
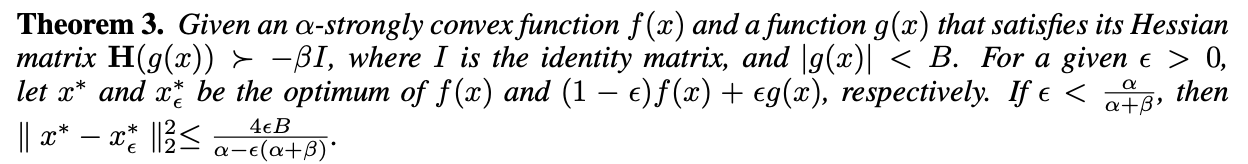
- 추가적으로 두 희소단어는 비슷한 최적해를 가지고, 따라서 비슷한 embedding을 가지게 된다.
Addressing the Problem
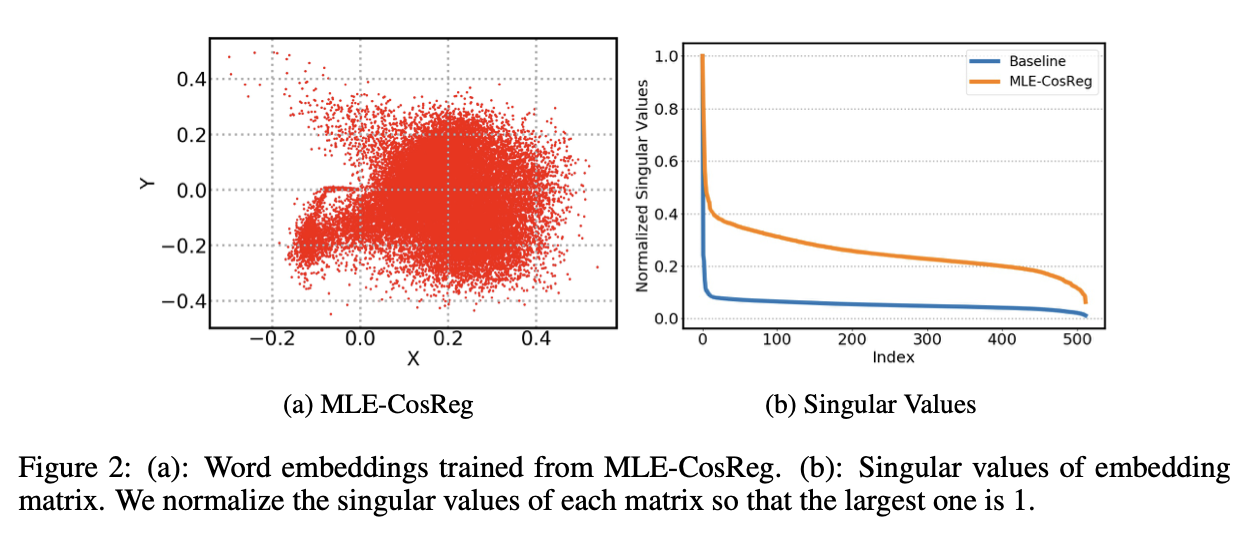
- 저자들은 이런 문제를 해결하고자, 직관적으로 narrow cone에서 벗어나고자 regularization term을 제안한다. narrow하게 한방향으로 분포한 것이 문제이므로 maximum angle between any two boundaries of the cone을 키우고자 한다. 이를 위해, cosine similarity를 최소화하는 방향으로 expressiveness를 최대화하고자 한다. 이 loss를 MLE-CosReg라고 명명한다.
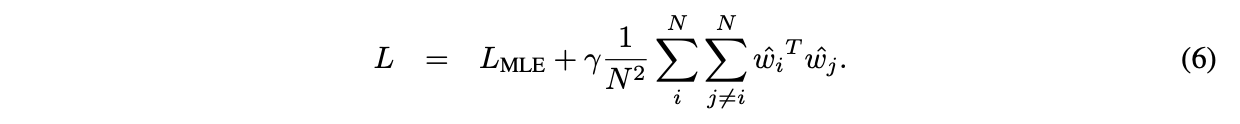
- 여기서 WW^T = 1이므로 eigen value의 합은 N이 된다. 따라서 Larges eigen value의 upper bound는 N이 될 것이다. 따라서 정규화항을 최소화하는 것은 이 upperbound를 줄이는 것과 같다. 즉, spectral radius를 최소화하는 것이라고 볼 수 있다.
Expereiment results
-
language modeling과 matchine translation에 대한 결과를 리포트한다.
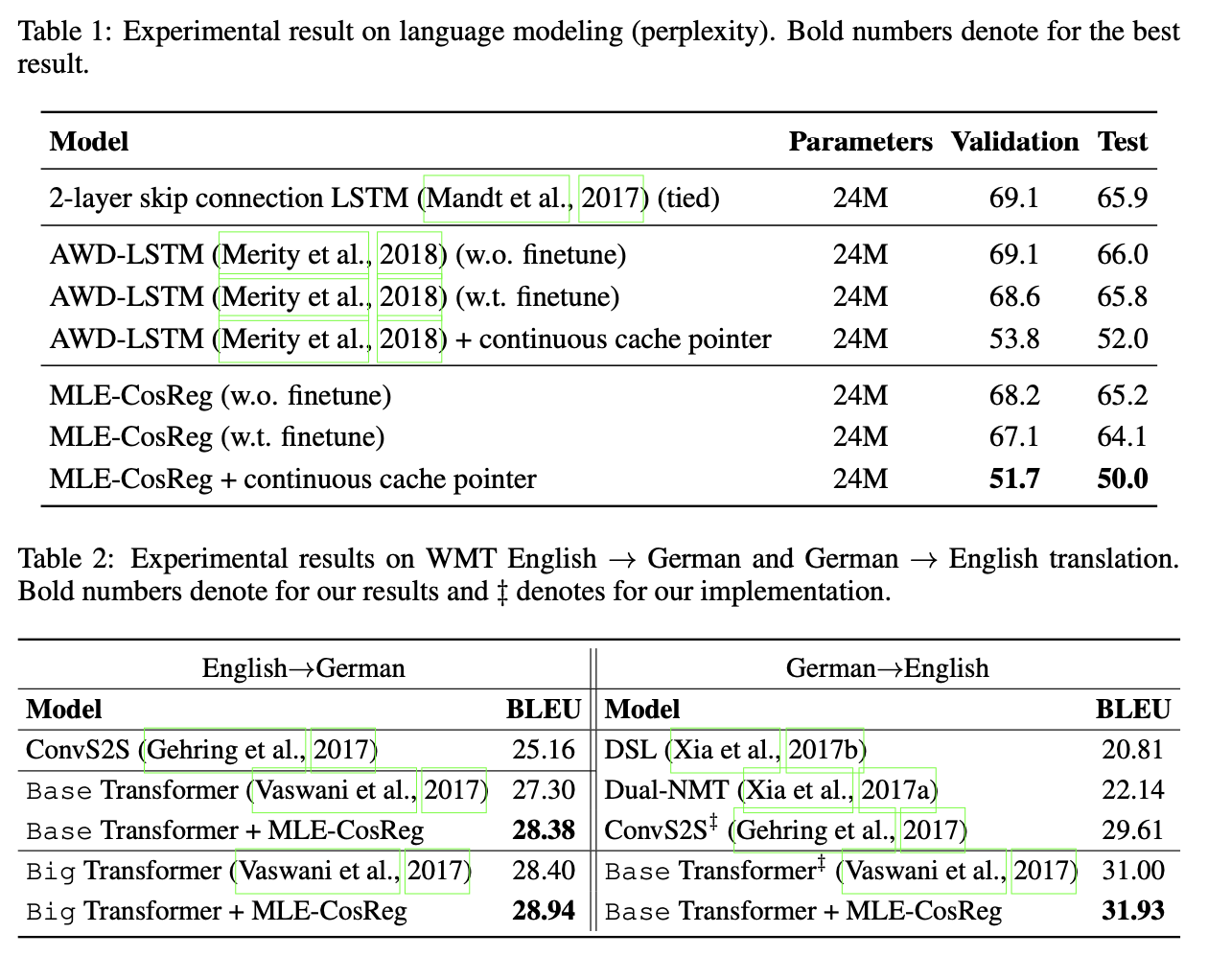
-
SVD 플롯 결과도 확인해보면 제안한대로 플롯이 더 고르게 분포하는 것을 볼 수 있다.