[논문리뷰] Selective Attention: Enhancing Transformer Through Principled Context Control

• 해당 논문은 Selective Self Attention layer을 통해서 기존 Key, value 에서의 sparsity 와 relevance control이 어려웠던 문제를 해결하고자 한다. Temperature을 각 임베딩에 적용하고, 이를 조절하는 과정을 이론적, 실험적으로 보이며 temperature scaling이
  • attention dilution 완화
  • optimization process 보정
  • softmax spikiness control
  • suppress irrelevant/noisy token
• 을 가능케함을 보인다.
• 여기서 attention dilution 이란, input sequence가 길어짐에 따라 attention distribution이 flat해지는 현상을 말한다.
• 특히, temperature scaling은 새로운 파라미터를 0.5% 추가하고, 심지어 weight sharing까지 적용해서 현존하는 LLM에 쉽게 적용할 수 있음을 강조한다.

Introduction

• 기본적으로 현재 모델들은 canonical self attention 을 통해 시퀀스 매핑을 진행한ㄴ다. 이를 수식으로 표현하면, $X \mapsto \mathbb{S}(QK^T)V$ 라고 쓸 . 수있다. (row wise softmax를 적용)
• 각 쿼리에 대해 이 프로세스로 query-dependent composition을 만들게 되는데, 이를 통해
  • semantic similarity 파악: 토큰 간 유사도. 키, 쿼리 임베딩 간의 각도로 파악
  • contextual sparsity 조절: spikiness of attention map으로 확인.
• 두가지 목표를 달성하고자 한다. 주로 두번째 목표는 attn map이 실제로는 sparse하게 나타나는 경우가 많기에 잘 조절하는 것이 중요하다.
• 그러나, 두 목표를 동시에 이루기는 어렵다(inflexible parameterization, 두 목표를 하나의 attention term으로 혼합된 상태에서 이루려 하기 때문임)
• 그러므로 Selective self attention은 semantic similarity와 contextual sparsity를 분리하려 한다.
  • $\mathbb{S}(\tau(q) \cdot Kq)$ 로 계산, $\tau(q)$는 inverse temperature. → key, query embedding matrix의 contextual sparsity를 조절하고자 함.
• Contribution
  • Query Selectivity: 더 작은 attn map parameter norm을 가지도록 만들어서 spikier attention map을 만들 수 있도록 해 attention dilution 완화
  • Value Selectivity: denoising perspective 에서 Noisy value suppression에 temperature scaling이 도움이 됨
  • Positional temperature: position 기준 scaling을 통해 length의 attention dilution 완화
  • Modularity and parameter-efficiency: weight sharing, small additional params
  • Empirical benefits : pretraining, fine-tuning 모두 좋은 결과
• 즉, sparse 한 attention map에서 꼭 capture 해야하는 신호를 더 “잘” 잡아낼 수 있도록 강조하는 효과를 보이며 smaller map으로 이를 가능케한다는 것!

Methodology

• 사실 방법론은 굉장히 간단한 편이다. 기존 Attention에 temperature term이 추가적으로 곱해진 것과 같다.
• 여기서 temperature은 element-wise곱을 통해 곱해져, 각 토큰마다 temperature을 부여한다.
• inverse temperature function $\tau(\cdot)$은 data-dependent 하며, 해당 논문에서는 scalar-value function으로 설정했다. (벡터가 딱히 더 좋은 성능을 보이지 않음) 또한, 이 값이 굳이 non-negative가 되도록 제한하지도 않았다.
• 결론적으로 SSA는 SGA, Scalar Gating Attention이라고도 표현할 수 있겠다!

Design choices

• Temprature scaling for query and value tokens
  • temperature function은 key, query, value에 각각 적용이 가능하며, 각각 다른 효과를 지닌다.
  • 구현 상으로는 key에는 temperature function을 적용하지 않았다.
  • 먼저 query temperature은 query의 위치와 임베딩에 연결된 attention map의 spikiness를 control한다.
  • value temperature은 불필요한 토큰의 영향력을 줄이고 context window의 aggregation 능력을 높인다.
  • key temperature을 query temperature과 동시에 설정하게 되면, cos-sim의 크기가 원래와 반대로 돌아갈 수 있으므로 오히려 기존의 semantic similarity 를 파괴할 수 있으므로 설정하지 않았다.
    • $cos(key1, query) > cos(key2, query) \rightarrow cos(key1, \tau(q) query) > cos(key2, \tau(q)query)$
    • $cos(\tau(k1) key1, query) ?? cos(\tau(k2) key2, query)$
• Token-aware and position-aware temperature scaling
  • $\tau(x) = \tau^{tok}(x) + \tau^{pos}(x)$
  • $\tau^{tok}(x) = tanh(f(x))$
    • f(x): 학습가능한 token 영향 조절 함수
    • tanh : -1~1, 0 모두 가능케함. 관련 없는 값은 0으로 supress 할 수 있도록함
  • $\tau^{pos}(x) = 1 + \sigma(\alpha)log(n)$,
    • n : position of token x in the sequence
    • $\alpha$ : paramter
    • $\sigma(\cdot)$ : sigmoid function, 함수값의 범위와 안정성 조절할 수 있도록 함
• Weight sharing
  • overhead를 줄이고자함.
  • Position-aware: 하나의 추가 파라미터로 충분함
  • Token-aware: f(x) 를 학습해야함.
    • $f(x) = \mathbf{W}_{tmp} \mathrm{GeLU}(\mathbf{W}^{'}_{tmp}x) = \mathbf{W}_{tmp} \mathrm{GeLU}(\mathbf{W}_{k/q/v}x)$
    • 기존 임베딩 행렬을 재사용하여 파라미터 수를 줄임
    • 또한 마지막 레이어부분만 알면 되므로 3개의 벡터만 저장하면됨 사실상!
  • 추가적으로 학습 없이 이미 주어진 데이터에 대해 특징을 가져다 사용 (ex. frequency) 방식도 괜찮음. 이 때는 무려 0.1% 오버헤드밖에 없음

Theoretical Insights into Selective attention

The benefits of incorporating query embedding

• Hinton (specific) Scientist (General) → similar semantic, different spikiness (specificity)
  • specificity: contextual sparsity of a query
  • $\mathrm{spec}_\mathbf{W}(q) := ||\mathbf{W}^\top q||$ : magnitude of query embedding
  • more sparse → high specificity → larger norm of query embedding(=operator norm of W)
• Lemma 1 : the attention weights are lower bounded by the ratio of specificity difference to semantic distance

• SSA : Lemma1 에서 만든 specificity와 동일 specificity를 달성하기 위해서 temperature과 KQ-weight를 아래와 같이 설정할 수 있다.
  • Effective weight matrix: $\mathbf{W} = \tau(q) \cdot \mathbf{W}_q\mathbf{W}_k$
  • $\tau(a) = L_a$, $\tau(b) = L_b$, $||W|| = 1$
  • 이 때, $W_a, W_b$의 upperbound가 $||W_a||, ||W_b|| \le \mathrm{max}(L_a, L_b)$인 상태로 원하는 specificity 를 달성할 수 있다.
• 즉, norm growth가 semantic distance로부터 분리되었음을 확인할 수 있다!
  

• 이로부터 우리는 query selection을 잘못한다면 model weight이 엄청 커질 수 있음을 알 수 있다. (upper bound가 없어지므로, 비슷한 쿼리에 다른 specificity를 할당할 수 있음) 여기서 bottleneck이 발생하게 되는데

  1. weight이 커질 수록 최적화 속도 감소 (vanishing softmax derivative)

  2. overfit, overly sensitive final model

     

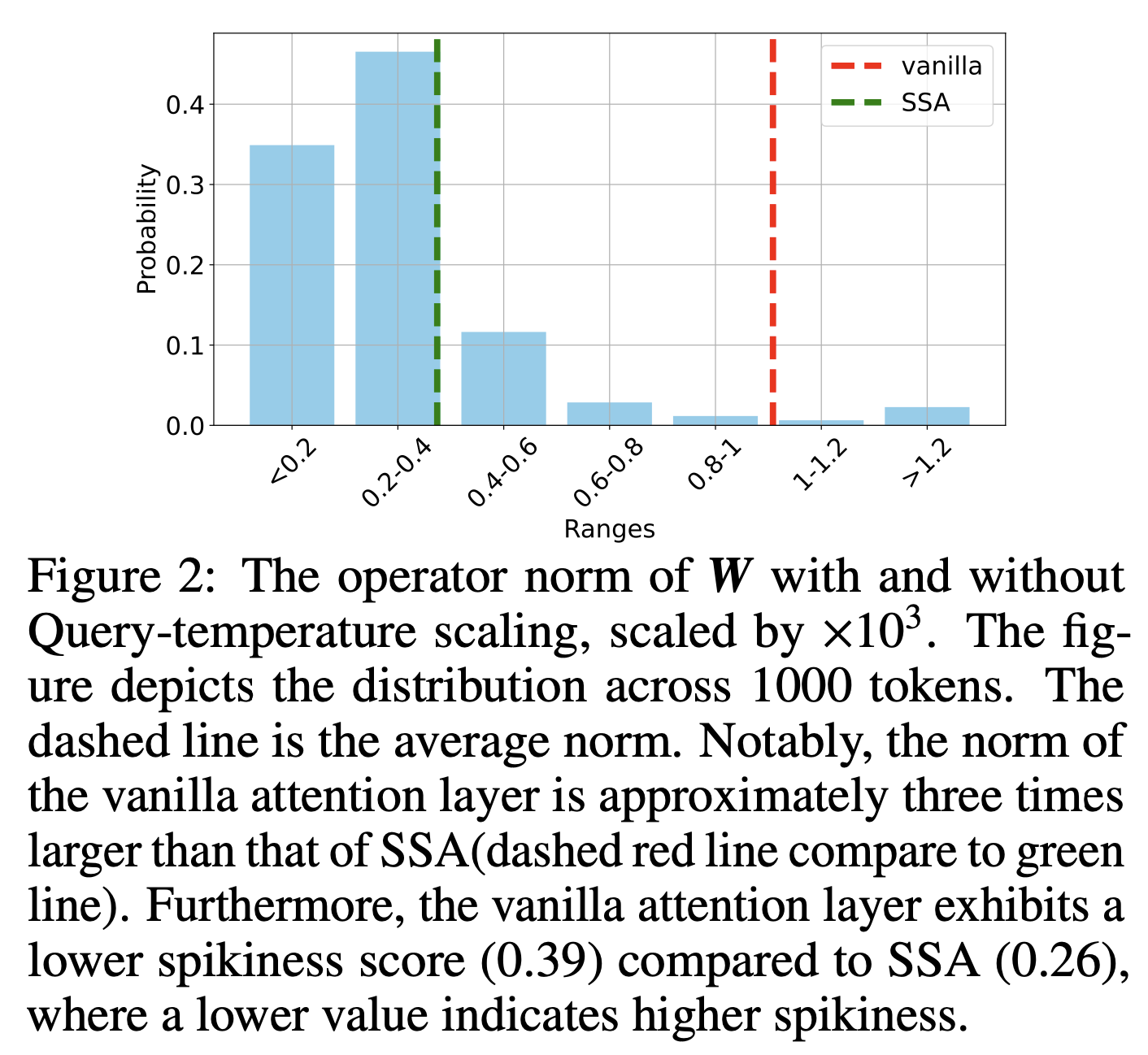
• 실험 결과 norm을 찍어봐도 selective attention의 attention weight이 sparse하면서도 더 작은 attention임이 확인 가능하다.

  • spikiness of attention map = $||s||_1 \over {||s||_2 L}$

• 같은 attention head도 더 빨리 특정 쿼리의 distinct/sparse attention을 파악하는 것이 가능해짐을 확인하고자 추가적인 실험을 진행한다.

  • 각 sequence에 대해 각 individual query와의 attention map을 구하면 아래와 같이 구할 수 있다
  • $E = [e_1, e_2, ..., e_K]^\top \in \mathbb{R}^{K \times d}$
  • $\mathtt{att}(E, W) = \mathbb{S}(EWE^\top)$, $\mathtt{att}(E, W) = \mathbb{S}(\tau(E) \odot EWE^\top)$
  • 여기서 softmax의 합이 1이 되므로 attention matrix가 stochastic matrix고, 따라서 markov chain transition matrix로 해석할 수 있다.
  • 그렇다면 Query-selective attention이 더 큰 클래스의 softmax attention을 표현할 수 있는가? 라는 질문이 생기게 된다. ….
  • 직관적으로, 더 다양한 spikiness variation across its rows를 보이면 이러한 행들을 더 잘 잡아낼 수 있을 거라 짐작할 수 있다.
  • 예를 들어, token generation experiment에서 salmonella 와 bacteria에 대해 생각해보자. 더 general한 bacteria가 더 많은 이웃을 가질 것이 자명하다.

• 확인을 위해 specificity를 기준으로 class를 구분하여 undirected graph를 만들어 둔다. 여기서 stochastic matrix $P^\star$를 얻을 수 있을 것이다. 이러한 $P^\star$를 추정하기 위해 token prediction 실험을 진행한다.

  1. input seq sampling
  2. $P^\star$ 기준으로 다음 토큰 결정
  3. 1-layer SSA 로 dynamics capture

• 결과적으로 cross entropy distance를 체크하여 salmonella가 왜 bacteria보다 낮은 temperature를 가지게 되는지를 설명할 수 있다.

• 추가적으로 이렇게 approximate한 결과와 $P^\star$ 간의 차를 err_map을 통해 확인한다. 확인해보면 SSA의 결과가 더 낮은 값을 가지며, 자연히 SSA가 fewer neighbors에 대해서 낮은 temperature를 assign한다는 직관과 일치한다.

• 좀 더 정리해서 Proposition으로 이어가보자.
  

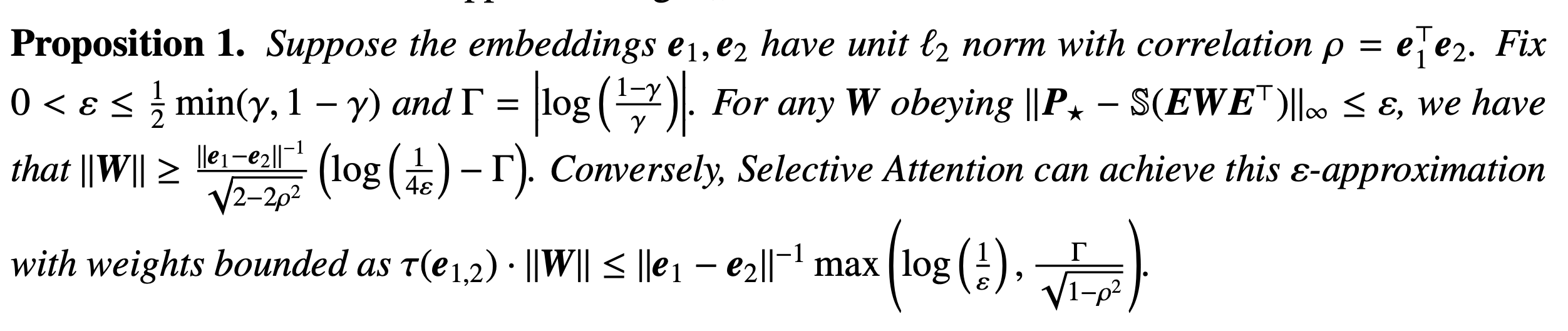
• Proof for proposition 1
  

The benefits of incorporating query position

• attention dilution을 해결하기 위해 query position이 필요하다. 그러나 softmax score은 upper bound가 존재한다.

  • $W = W_q W_k$, $s^L = \mathbb{S}(XW^\top x_L)$
  • $||s^L||_{l_\infin} \le \frac{1}{1+(L-1)e^{-2||W||}}$
  • 즉 이 값이 상수이려면, spectral norm growth rate of ||W|| 가 lower bound가 존재해야함을 알 수 있다. 이 lower bound는 $||W|| \ge 0.5logL + O(1)$ 로 잡을 수 있다.

• Feature imbalance setting에서 optimal temperature scaling이 없으면 풀 수 없는 task에 대해 생각해보자.

  • feature imbalance: 중요하지 않지만 자주 나오는 토큰 (ex. is) 가 중요하지만 덜 자주 나온 토큰에 비해 집중받는 경우

  • Imbalanced token setup

    • $X = [x_1, x_2,...,x_L]^\top, \ x_i \in {a, b},\ a\in \mathbb{R}^d,\ b \in \mathbb{R}^d, \ y = \alpha a + (1-\alpha) b, \ \alpha \in (0,1)$
    • a = majority token, b = minority token
    • y와 attention output 간의 loss 를 minimize 한다!
      

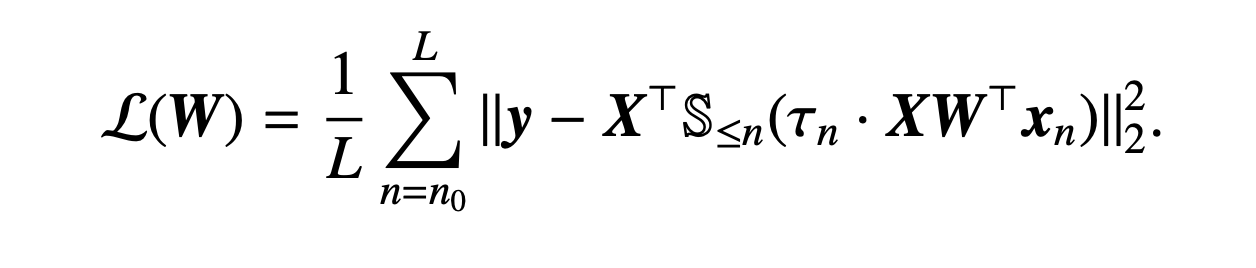
  • 여기서 proposition 2가 등장한다.

    

    • proof for proposition 2
      

    • 따라서 n이 증가할수록 불필요한 토큰을 가지고 있게 되어 relation 의 역인 k_n 의 증가로 이어진다. $k_n$ 이 power law를 따른다고 하면 temperature sacling rule은 아래와 같다.

      • $\tau_n = \mathtt{const} + \mathtt{pow} \cdot \mathrm{log}(n)$

    • 따라서, position-aware scaling rule은 이러한 특성을 반영하여 logarithmic 하게 설계되었다.

The benefits of incorporating value embedding

• Value embedding은 단순히 선형변환이므로, 어더한 토큰의 기여도는 attention score에 기반한 weighted sum이다. value temeprature scaling은 non-linear scalar weighting function으로 작용하며, temperature을 조정하여 각 토큰의 영향력을 조절할 수 있도록 한다.

• 이러한 장점을 Denoising task에서 확인할 수 있다.

• Task setup
  

  • 전체 토큰 중에서 parameter $\alpha$ 에 따라 signal token (noise + e_q) 의 개수가 결정된다.
  • objective는 정답값과 norm값 사이의 차이를 줄이는 형태로 작동한다.
  • 문제를 풀기 위해 attention model은 denoised target을 추정하고자 적절히 토큰을 섞어야 하는데, q가 uniform하므로 signal token으로도 전체 space를 커버할 수 있다. 즉, Linear한 projection만으로는 문제를 풀 수 없다. (전부 같은 값으로 보이니까) 따라서 nonlinear mapping이 필요하다.

• 따라서, 이를 해결하기 위해 여러가지 nonlinear 방법을 활용했다.

  • vanilla attention : 기본 어텐션
  • value-selective self attention : 논문에서 제안하는 SSA
  • naive averaging : 단순 평균
  • bayes optimal estimator : 베이즈 최적 추정량: 정답 set으로 normalize하여 ground truth set of signal token을 얻음
  • 실험 결과를 보면 잘 하는걸 볼 수 있다!
    

Empirical Evaluations

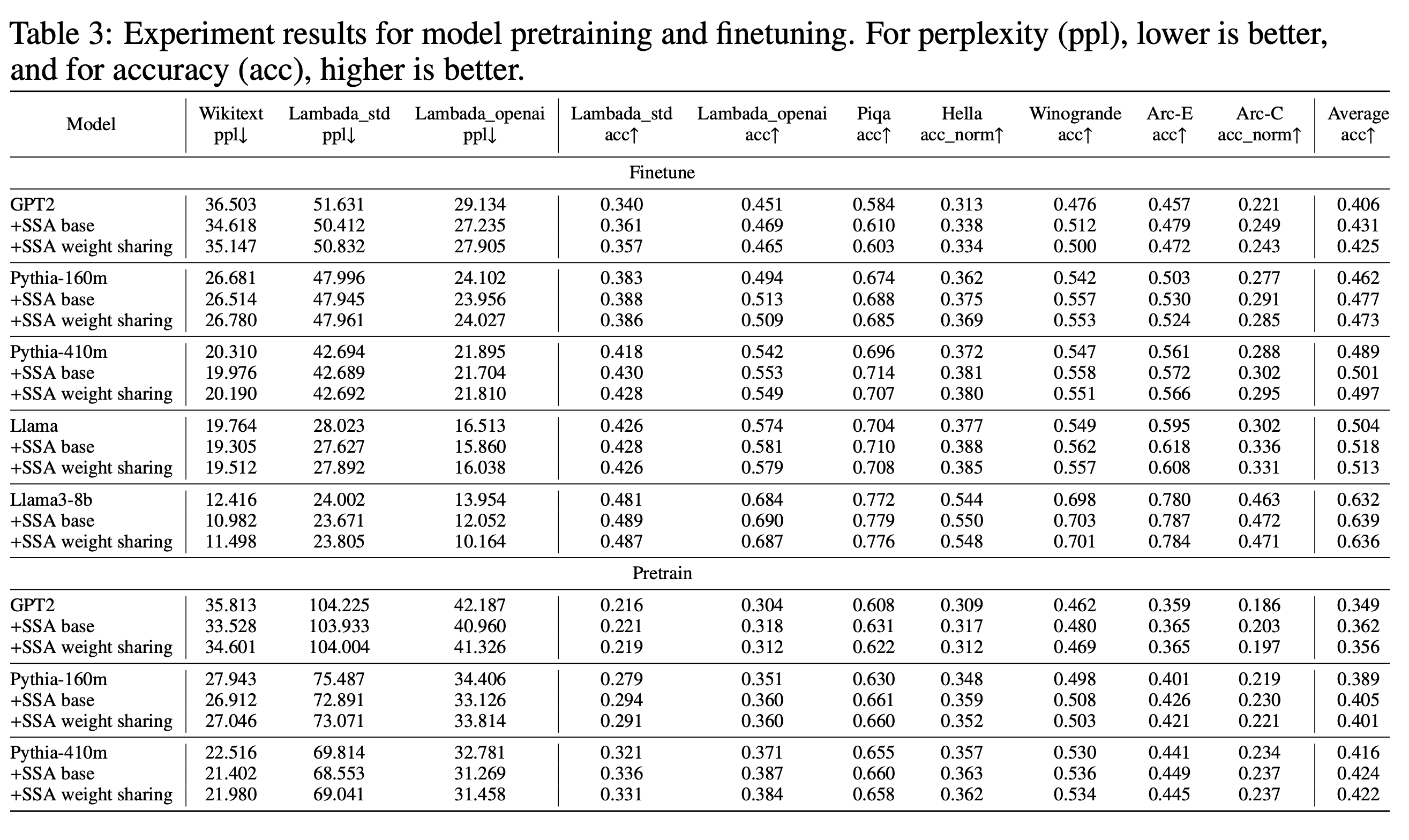
• Standard benchmarks

  • pretraining and finetuning
  • 다른 방식으로 SSA를 진행한 결과도 함께 담았다. 나쁘지 않은 결과를 보였음

• Passkey retrieval
  

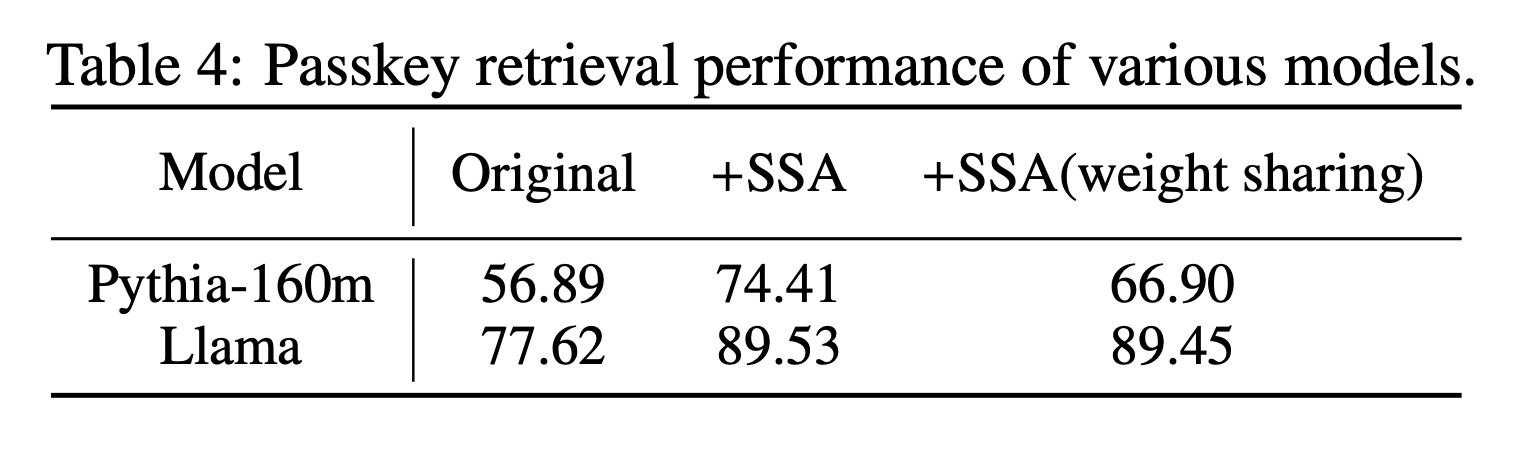
  • 기본 모델보다 SSA 추가한 결과가 더 좋았음. weight sharing 안한게 더 좋은 결과를 보임

• Ablations

  • token-aware, position-aware
    

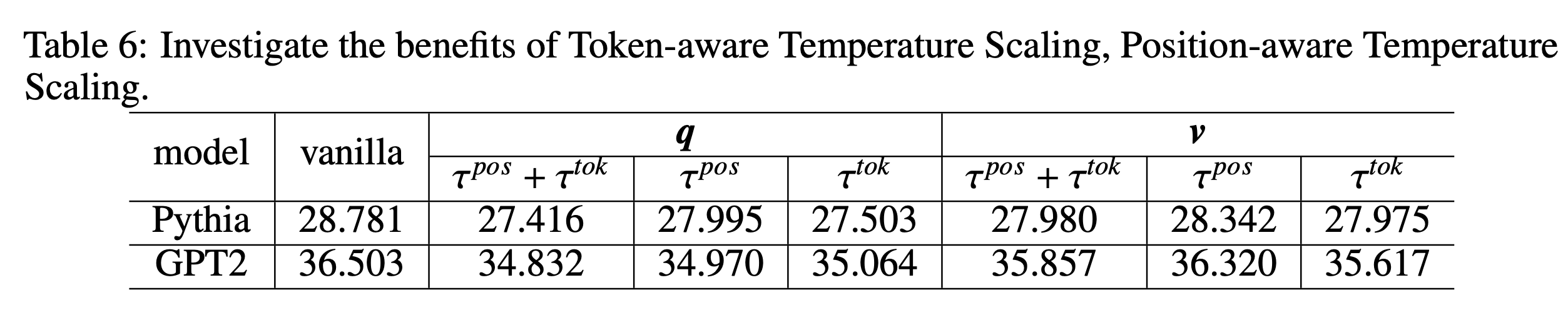
  • weight-sharing, feature-based
    

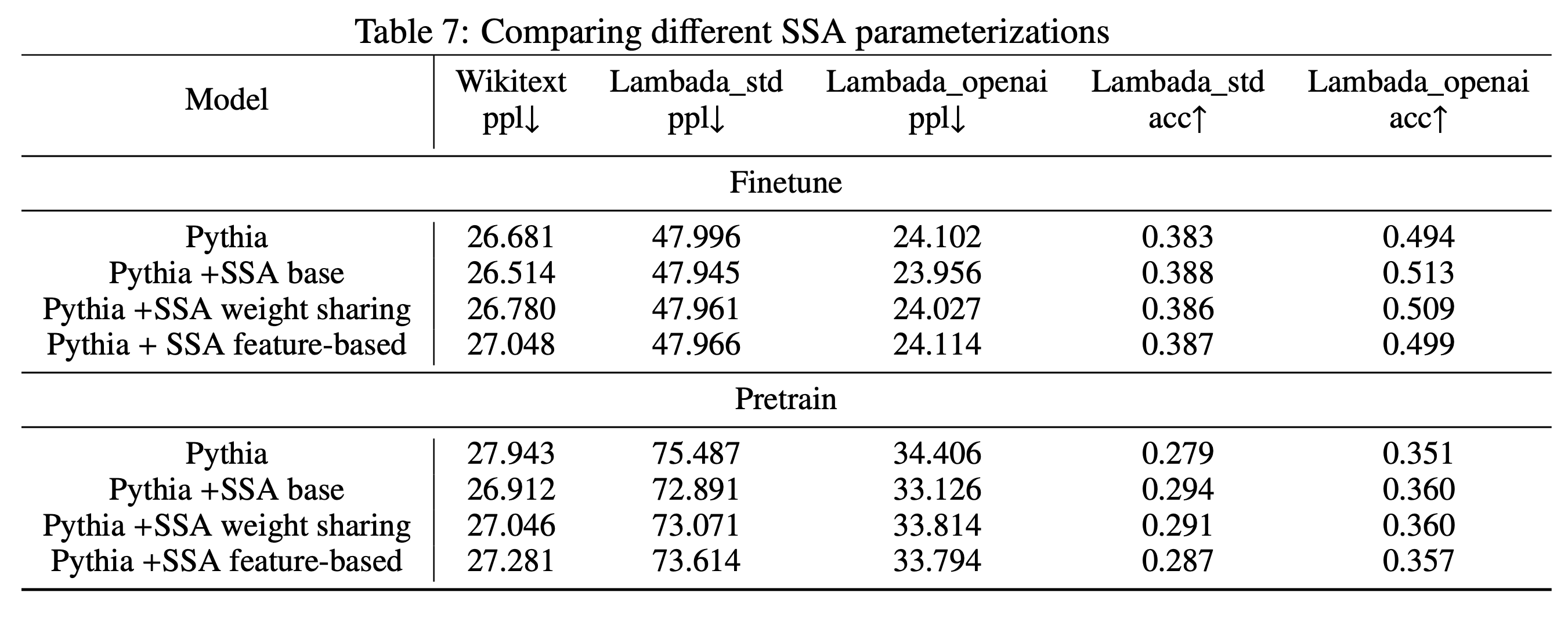
  • different-function
    

Furthre Discussion

Sparsity and temperature

• fixed attention row, let
  

• 이 때 sparsity와 temperature scaling 간의 관계는 분명하다. 예를 들어, top entry의 temperature가 감소한다면, entropy는 증가할 것이다. power-law assumption을 기반으로, 어떠한 attention이 2개의 값을 fraction of larger attention score로 파악한다고 해보자.
  
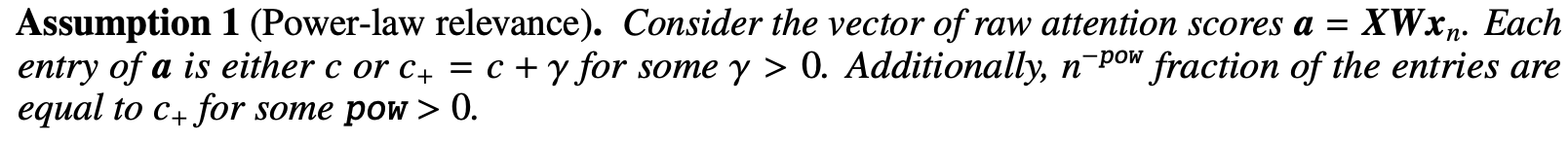
  - c+: score attained by salient token
  - gamma : score advantage of salient tokens over rest of tokens
  - pow : fraction of salient tokens

• Lemma
  

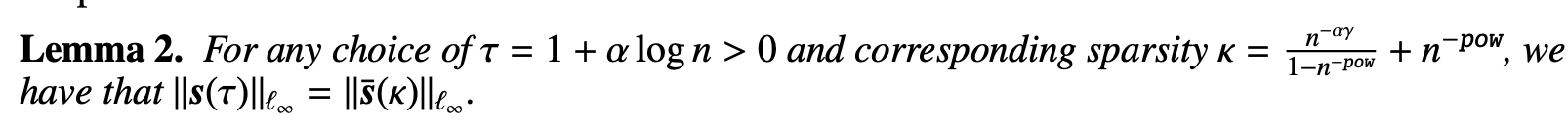
• proof of Lemma 1
  

  • TS 와 sparse-attention이 동일한 softmax temperature behavior를 갖는다
  • 따라서 scaling 과 sparsification이 특정한 관계를 가진다고 볼 . 수있다. 결국 power law decay에 다라서 sparsification rule을 정리할 수 있다.
  • 결국 SSA를 통해 sparse attention을 목표하지 않고, spikiness를 목표했음에도 종국에는 sparse attention과 같은 effective sparsity에 도착할 수 있음을 생각해볼 수있다.