220114 - 멀리 뛰기

◾ 멀리 뛰기 : 프로그래머스 LEVEL 3

• https://programmers.co.kr/learn/courses/30/lessons/12914

문제

효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다. 칸이 총 4개 있을 때, 효진이는
(1칸, 1칸, 1칸, 1칸)
(1칸, 2칸, 1칸)
(1칸, 1칸, 2칸)
(2칸, 1칸, 1칸)
(2칸, 2칸)
의 5가지 방법으로 맨 끝 칸에 도달할 수 있습니다. 멀리뛰기에 사용될 칸의 수 n이 주어질 때, 효진이가 끝에 도달하는 방법이 몇 가지인지 알아내, 여기에 1234567를 나눈 나머지를 리턴하는 함수, solution을 완성하세요. 예를 들어 4가 입력된다면, 5를 return하면 됩니다.

---

입력

• n은 1 이상, 2000 이하인 정수입니다.

출력

• 끝에 도달하는 방법 % 1234567

입출력 예

n	result
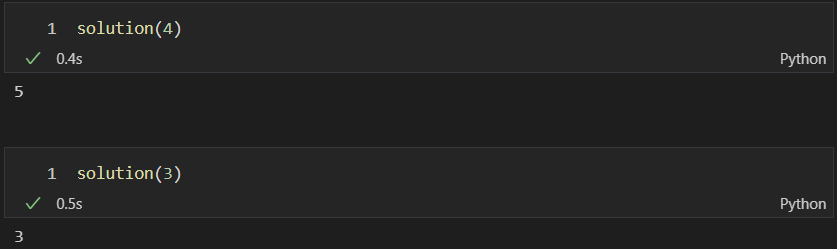
4	5
3	3

---

◾ 풀이

1. 해설

• 동적 계획법(Dynamic Programming)을 이용하여 해결할 수 있다.
• 특정 n에 도착할 수 있는 경우의 수는 [(n-1에 도착하는 경우의 수) + 1칸, (n-2에 도착하는 경우의 수) + 2칸]이 있다.
  • f(n) = f(n-1) + f(n-2) (단, n > 2)
  • f(1) = 1칸 => 1개
  • f(2) = (1칸, 1칸), (2칸) => 2개
• 반복문을 통해 n까지 칸을 늘려가며 도달할 수 있는 경우의 수를 구하면 된다.

---

2. 프로그램

1. dp 초기화
   • index : 0 ~ n으로 설정
   • index 0, 1 : 1로 초기화
2. n이 2이상일 때 반복을 통해 n까지의 결과를 차례로 계산
   • 계산시 %1234567 연산 진행
3. dp[n] 반환

# 코드
def solution(n):
    answer = 0
    dp = [0] * (n+1)    # dp 생성
    dp[0], dp[1] = 1, 1 # dp 초기화
    # n까지의 결과 차례로 계산
    for idx in range(2, n+1):
        # 결과에 %1234567 연산 진행
        dp[idx] = (dp[idx-1] + dp[idx-2]) % 1234567

    # dp[n] 반환
    answer = dp[n]
    return answer