머신 러닝 - Iris Classification(2)

◾Decision Tree

• Decision Tree : 분류 및 회귀에 사용되는 비모수 지도 학습 방법
  • 목표는 데이터 특성에서 추론된 간단한 결정 규칙을 학습하여 대상 변수의 값을 예측하는 모델을 만드는 것입니다. 트리는 조각별 상수 근사값으로 볼 수 있습니다.
  • 데이터 전처리를 하든 하지않든 큰 영향이 없다.
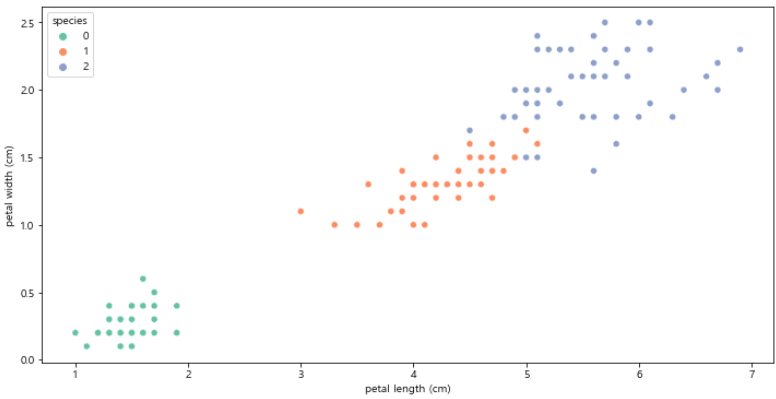
• setosa의 경우 쉽게 구분이 가능하나 versicolor, virginica의 구분을 어떻게 할지?

# petal length, petal width 분포도
plt.figure(figsize = (12, 6))
sns.scatterplot(x='petal length (cm)', y = 'petal width (cm)', 
                data = iris_pd, hue='species', palette='Set2')
plt.show()

• 1번, 2번 IRIS만 선택

# 두 개 IRIS에 대한 분포도
# 데이터 변경
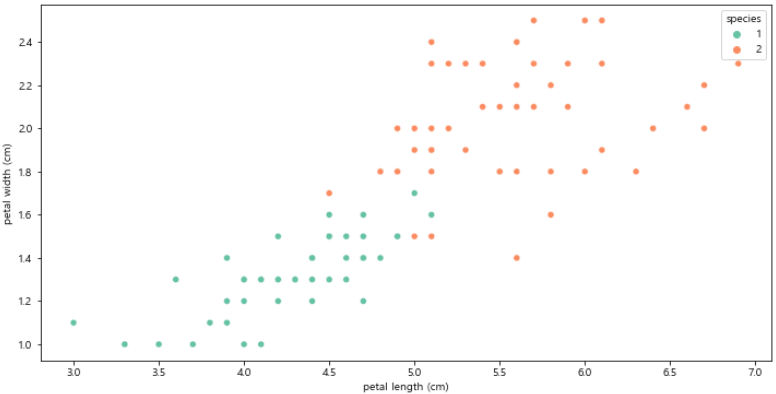
iris_12 = iris_pd[iris_pd['species'] != 0]
# 경계선을 어떻게 해야 최소의 오류가 발생할지 고민
plt.figure(figsize = (12, 6))
sns.scatterplot(x='petal length (cm)', y = 'petal width (cm)', 
                data = iris_12, hue='species', palette='Set2')
plt.show()

• Decision Tree의 분할 기준(Split Criterion)
  • 정보 획득(Informatin Gain) : 정보의 가치를 반환하는데 발생하는 사전의 확률이 작을수록 정보의 가치는 커진다. 정보 이득이란 어떤 속성을 선택함으로써 인해서 데이터를 더 잘 구분하게 되는 것.
  • 엔트로피(entropy) : 열역학의 용어로 물질의 열적 상태를 나타내는 물리량 단위 중 하나로 무질서의 정도를 나타낸다. 얼마만큼의 정보를 담고 있는지, 무질서도(disorder)과 불확실성(uncertainty)를 나타낸다.
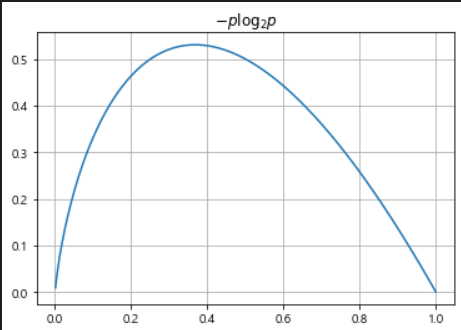
• 엔트로피 : $Entropy = \sum_{k=1}^{m} {-p_{i}\log_{2}{p_{i}}}$
• $-p_ilog_{2} p_{i}$
  • p는 해당 데이터가 해당 클래스에 속할 확률
  • 어떤 확률 분포로 일어나는 사건을 표현하는데 필요한 정보의 양
  • 값이 커질수록 확률 분포의 불확실성이 커지며 결과에 대한 예측이 어려워진다.

# 엔트로피 그래프
import numpy as np

p = np.arange(0.001, 1, 0.001)
plt.plot(p, -p*np.log2(p))
plt.grid()
plt.title('$-p\\log_{2} p$')
plt.show()

• 빨간공 10개, 파란공 6개일 경우
• $Entropy = 빨간공~엔트로피 + 파란공~엔트로피$
• (10/16)np.log2(10/16) - (6/16)np.log2(6/16)
• 그룹이 나누어진 경우의 엔트로피
  • $Entropy = \sum_{i=1}^{d}{R_{i}}\sum_{k=1}^{m}{-p_{i}\log_{2}{p_{i}}}$
• 빨간공 7개, 파란공 1개 : 그룹1
• 빨간공 3개, 파란공 5개 : 그룹2
• 0.5(-(7/8)np.log2(7/8) - (1/8)np.log2(1/8)) + 0.5(-(3/8)np.log2(3/8) - (5/8)np.log2(5/8))
  • 엔트로피가 내려갔으므로 분할하는 것이 좋다.
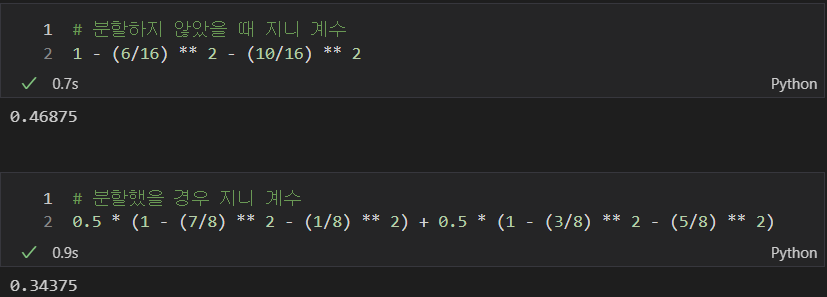
• log 계산의 불편성을 개선하고자 지니 계수 사용
• 지니 계수 : Gini index 혹은 불순도율
  • $Gini = \sum_{i=1}^{d}{R_{i}\{1 - \sum_{k=1}^{m}{-p^{2}_{ik}}\}}$
  • 엔트로피의 계산량이 많아서 비슷한 개념이면서 보다 계산량이 적은 지니 계수를 사용하는 경우가 많다.
    
• Frame Work
  • 5~6년 전만하더라도 하드 코딩으로 작성
  • Lab에서만 사용되는 코드 체계가 있고 서로만 공유하며 사용
  • SW적 개발 도구의 확산과 공유 등으로 공개적인 Frame Work로 발전

---

◾Scikit Learn

• Scikit Learn
  • 2007년 구글 썸머 코드에서 처음 구현
  • 현재 파이썬에서 가장 유명한 기계 학습 오픈 소스 라이브러리
  • https://scikit-learn.org/stable/
• sklearn의 DecisionTreeClassifier로 구현

# scikit learn 결정 나무(decision tree) 구현
from sklearn.tree import DecisionTreeClassifier

iris_tree = DecisionTreeClassifier()
# 데이터 학습(fit)
iris_tree.fit(iris.data[:, 2:], iris.target)

• sklearn의 accuracy_score로 성과(정확성) 확인

# Accuracy 확인
from sklearn.metrics import accuracy_score

# 데이터 예측
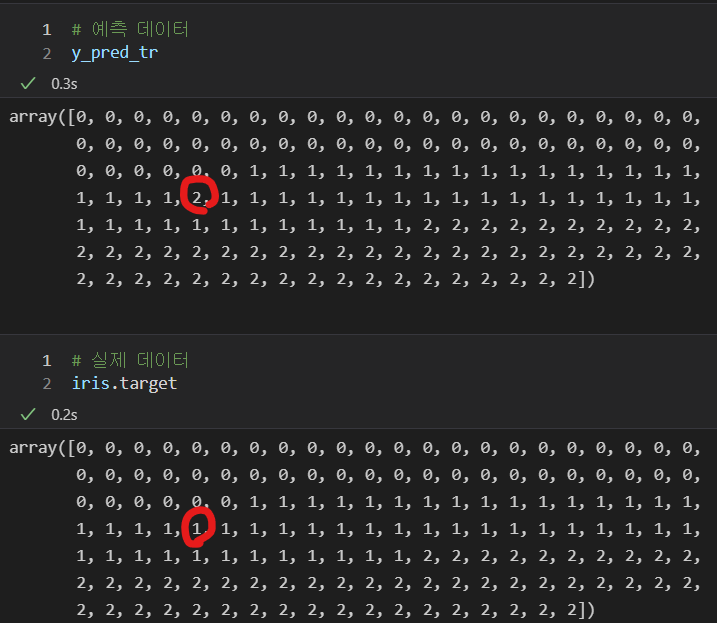
y_pred_tr = iris_tree.predict(iris.data[:, 2:])
# 정확성 확인
accuracy_score(iris.target, y_pred_tr)

• 데이터 확인 : 하나의 값을 제외하곤 일치하는 것을 볼 수 있다.