머신 러닝 - 회귀

◾Basic of Regression

• 일반적인 문제 해결 절차
  • 문제 파악 -> 규칙 선정 -> 평가 -> (에러 분석) -> ...(반복)... -> 출시
• 데이터 기반 문제 해결 절차
  • 문제 파악 -> ML/DL 알고리즘 훈련(데이터 사용) -> 평가 -> (에러 분석) -> ...(반복)... -> 출시
  • 모델 스스로 데이터를 기반으로 변화에 대응할 수 있다.
    • 데이터 업데이트 -> 훈련 -> 평가 -> ...
  • 머신 러닝(딥러닝)의 결과로 부터 문제를 더 많이 이해할 수도 있다.
• 지도 학습 : 정답이 있는 데이터를 이용해 학습시킨 후 새로운 데이터 적용
  • 분류(Classification) : 결과가 카테고리별로 나뉘는 경우
  • 회귀(Regression) : 결과가 연속적인 수치(Continuous Value)로 나오는 경우
• 비지도 학습 : 정답이 주어지지않는 데이터를 이용해 학습
  • 군집 : 비슷한 특성끼리 그룹을 만든다.
  • 차원 축소 : 많은 특성(라벨)을 줄여 시각화하고 계산의 양을 줄여 효율성을 높이는 것

1. 회귀

• Regression(회귀) : 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법(결과를 연속된 값으로 예측하는 것)
  • 데이터셋 -> 학습 -> Hypothesis(가설 = 모델) h
  • 선형 회귀(Linear Regression) : 입력 변수(특징)이 하나인 경우 주어진 학습 데이터와 가장 잘 맞는 함수(모델)h를 찾는다.
    • $h_{\theta}(x) = \theta_{0} + \theta_{1}x$
    • 기울기와, y절편을 찾아야한다.

2. OLS

• OLS(Ordinary Linear Least Square) : 최소제곱법으로 어떤 계의 해 방정식을 근사적으로 구하는 방법으로 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법이다.
  • $Y=AX$, $Y = \left(\begin{matrix} y_1 \\ y_2 \\... \\ y_n \end{matrix} \right)$, $A = \left(\begin{matrix} x_1 & 1 \\ x_2 & 1 \\... \\ x_n & 1 \end{matrix} \right)$, $X = \left(\begin{matrix} a \\ b \end{matrix} \right)$
  • 찾고 싶은 모델 : $f(x) = ax+b$
  • 행렬 정리
    • $A^{T}AX = A^{T}Y$(행렬A를 정방 행렬로 만들어 주기 위해)
    • $X = (A^{T}A)^{-1}A^{T}Y$
  • $E = [실제값1 - f(1)]^{2} + [실제값2 - f(2)]^{2} + ... + [실제값n - f(n)]^{2}$

3. OLS 실습

# 데이터 준비
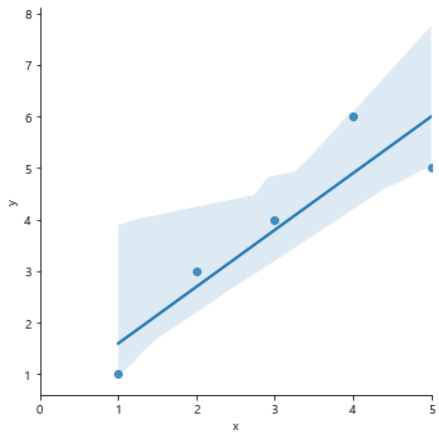
import pandas as pd

data = {'x' : [1., 2., 3., 4., 5.], 'y':[1., 3., 4., 6., 5.]}
df = pd.DataFrame(data)
df

# 가설 준비
import statsmodels.formula.api as smf

# formula : 'y ~ x' : 식이 [ y = ax + b ] 라는 의미
lm_model = smf.ols(formula='y ~ x', data=df).fit()

# 결과 확인
lm_model.params

# 그래프 그리기
import matplotlib.pyplot as plt
import seaborn as sns
import set_matplotlib_korean

sns.lmplot(x='x', y='y', data=df, height=5);
plt.xlim([0, 5]);

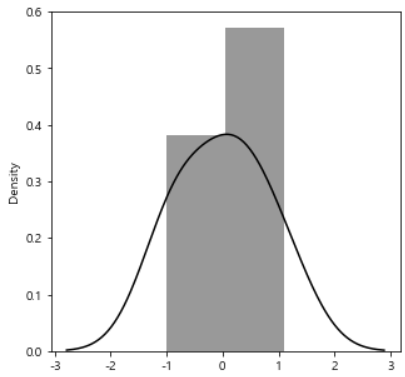
• 잔차 평가(residue)
  • 잔차는 실제값과 측정값의 차이를 말한다.
  • 잔차는 평균이 0인 정규분포를 따르는 것이여야한다.
  • 잔차 평가는 잔차의 평균이 0이고 정규분포를 따르는지 확인한다.

# 잔차 확인
resid = lm_model.resid
resid

• 결정 계수(R-Squared) : 예측값에서의 평균 제곱의 합을 실제값에서의 평균과의 오차 제곱의 합으로 나눈 값
  • 예측 값과 실제 값이 일치하면 결정 계수는 1이 된다.(결정 계수가 높을 수록 좋은 모델)
  • $\hat{y}$ : 예측된 값
  • $R-Squared(R^{2}) = {ssR \over ssT} = {{\sum_{i=1}^{n}{(\hat{y}-\mu)^{2}}\over {\sum_{i=1}^{n}{(y-\mu)^{2}}}}}$

# numpy를 이용한 결정 계수 계산
import numpy as np

mu = np.mean(df.y)
y = df.y
yhat = lm_model.predict()
# np.sum((yhat - mu)**2) / np.sum((y - mu) ** 2) 
lm_model.rsquared

plt.figure(figsize=(5, 5))
sns.distplot(resid, color='black')
plt.show()

---

◾통계적 회귀

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import set_matplotlib_korean

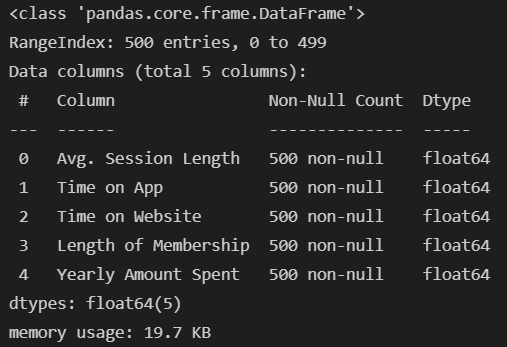
• 데이터 구조
  • Avg. Session Length : 한번 접속시 평균 사용 시간
  • Time on App : 앱 접속 시 유지 시간(분)
  • Time on Website : 웹 접속 시 유지 시간(분)
  • Length of Membership : 회원 자격 유지 기간(년)
  • Yearly Amount Spent : 연간 사용 금액

# 데이터 로드
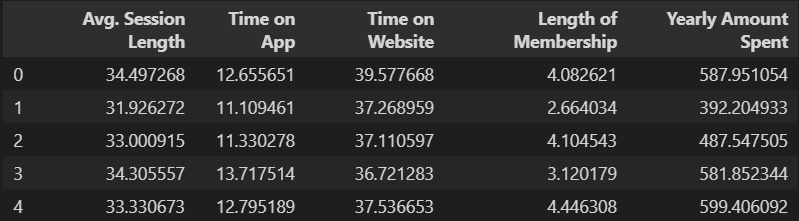
data = pd.read_csv('ecommerce.csv')
data.head()

# 컬럼 확인
print(data.columns)

# 필요없는 컬럼 삭제
data.drop(['Email', 'Address', 'Avatar'], axis=1, inplace=True)
data.info()

# 데이터 재확인
data.head()

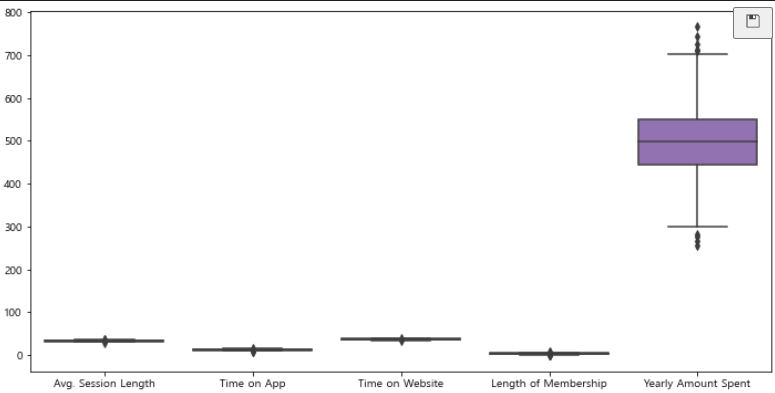
• Yearly Amount Spent 컬럼의 값이 차이가 심해 확인하기 힘들다.
• 제외하고 나머지 값들만 다시 확인

# 컬럼별 boxplot 확인
plt.figure(figsize=(12, 6))
sns.boxplot(data=data)
plt.show()

• 특별한 이상값은 확인할 수 없다.

# 컬럼별 boxplot 확인
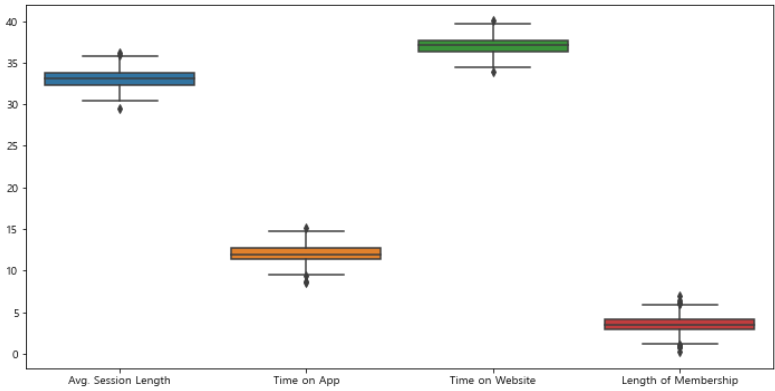
plt.figure(figsize=(12, 6))
sns.boxplot(data=data.iloc[:, :-1])
plt.show()

# 컬럼별 boxplot 확인
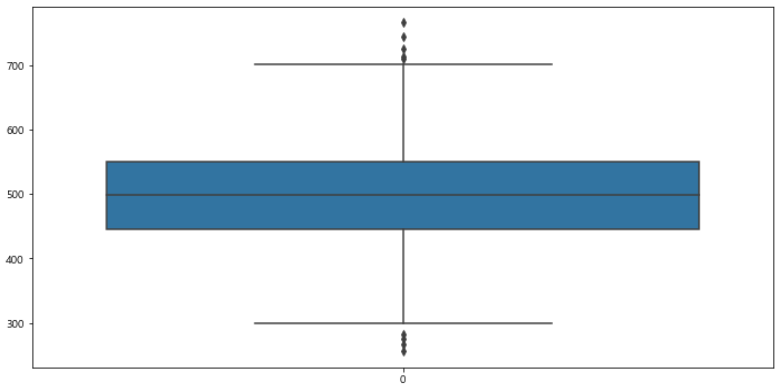
plt.figure(figsize=(12, 6))
sns.boxplot(data=data['Yearly Amount Spent'])
plt.show()

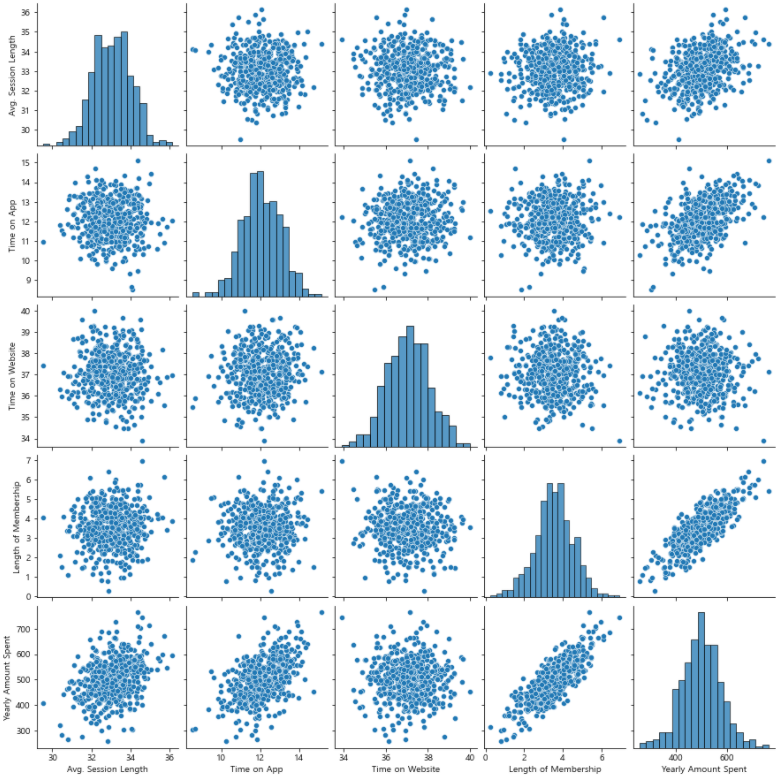
• pairplot을 이용해 경향 확인
  • Length of Membership와 Yearly Amount Spent 사이의 양의 상관관계 확인

sns.pairplot(data=data);

• lmplot을 이용해 Length of Membership와 Yearly Amount Spent 자세히 확인

# 상관계수 확인
plt.figure(figsize=(10, 5))
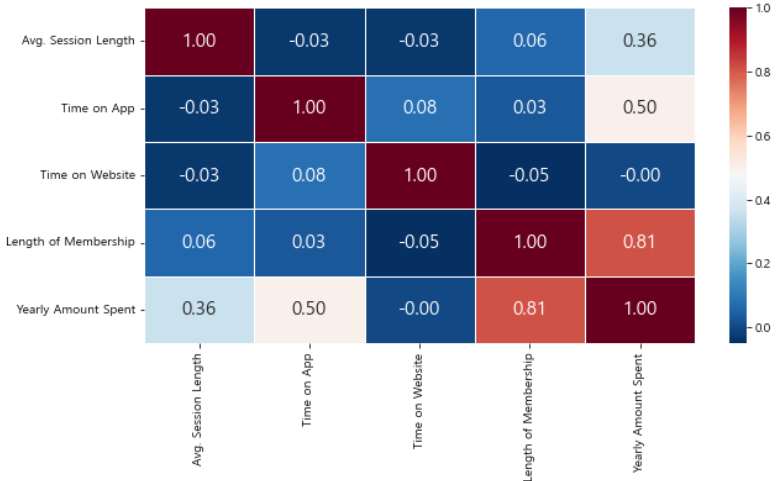
sns.heatmap(data = data.corr().round(2), 
            annot=True, fmt='.2f', linewidths=.5,
            cmap='RdBu_r', annot_kws={"size": 15})
plt.show()

# lmplot
sns.lmplot(x='Length of Membership', y='Yearly Amount Spent', data=data);

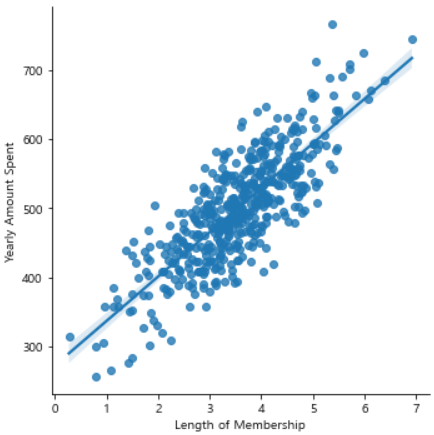
• 상관관계가 있는 멤버쉽 유지기간만 이용해 통계적 회귀
• 수치 해석
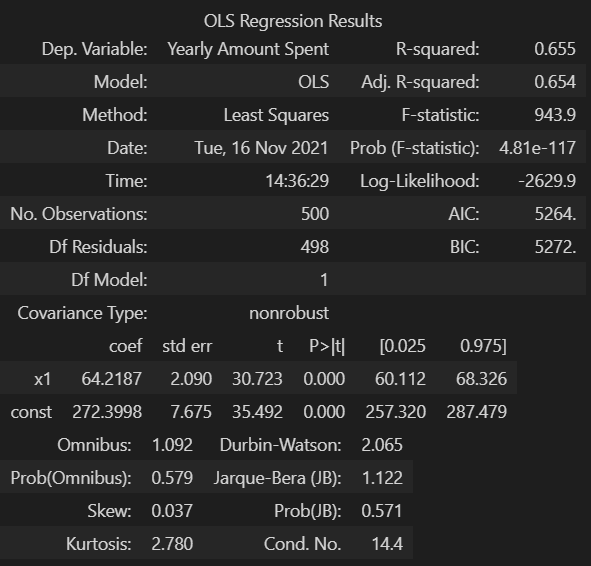
  • R-squared : 모형 적합도, y의 분산을 각각의 변수들이 약 99.8로 설명할 수 있음
  • Adj. R-squared : 독립 변수가 여러 개인 다중 회귀 분석에서 사용
  • Prob (F-statistic) : 회귀 모형에 대한 통계적 유의미성 검정
    • 0.05이하의 값이라면 모집단에서도 의미가 있다고 볼 수 있다.

# 통계적 회귀
import statsmodels.api as sm

X = data['Length of Membership']
y = data['Yearly Amount Spent']

lm = sm.OLS(y, X).fit()

# 회귀 리포트
lm.summary()

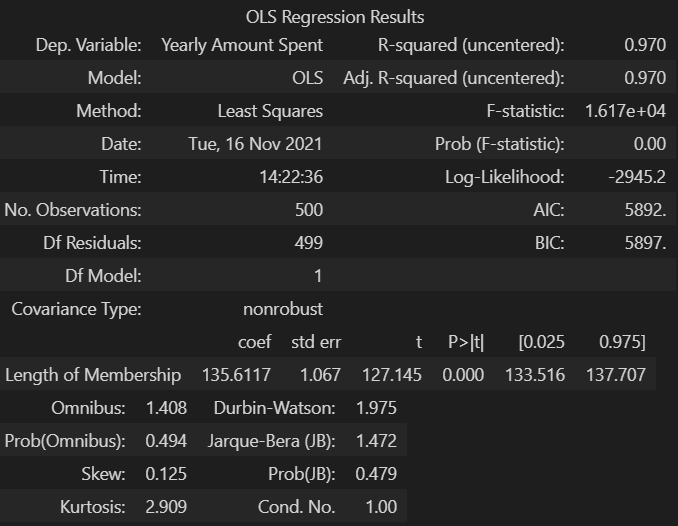
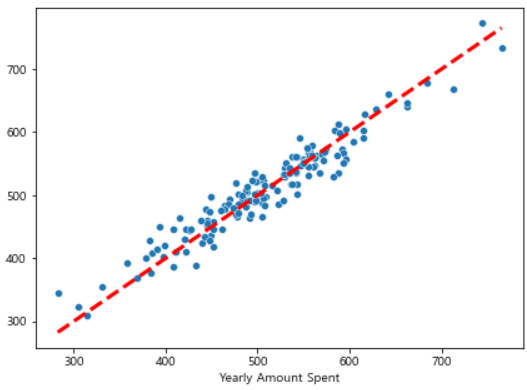
• 상수항이 없기 떄문에 아래와 같이 (0, 0)에서 시작한다.

# 회귀 모델 그리기
pred = lm.predict(X)

plt.figure(figsize=(7, 5))
sns.scatterplot(x=X, y=y)
plt.plot(X, pred, 'r', ls='dashed', lw=3)
plt.show()

# 회귀 모델 그리기
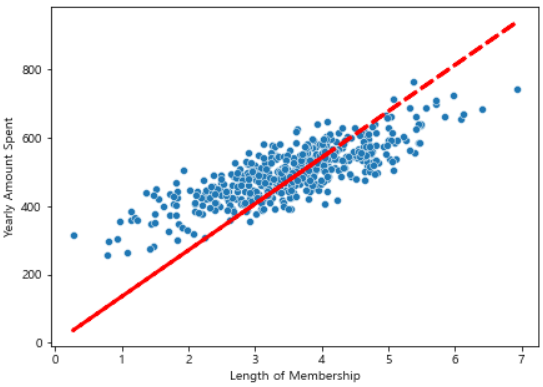
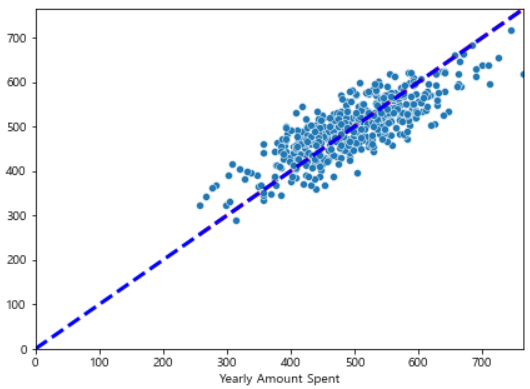
pred = lm.predict(X)

plt.figure(figsize=(7, 5))
sns.scatterplot(x=y, y=pred)    # 참값과 예측값 보여주는 것
plt.plot([min(y), max(y)], [min(y), max(y)], 'r', ls='dashed', lw=3)
plt.plot([0, max(y)], [0, max(y)], 'b', ls='dashed', lw=3)
plt.axis([0, max(y), 0, max(y)])
plt.show()

# 상수항 추가하기
X = np.c_[X, [1]*len(X)]
# 다시 학습
lm = sm.OLS(y, X).fit()
# 회귀 리포트
lm.summary()

# 선형 회귀 결과
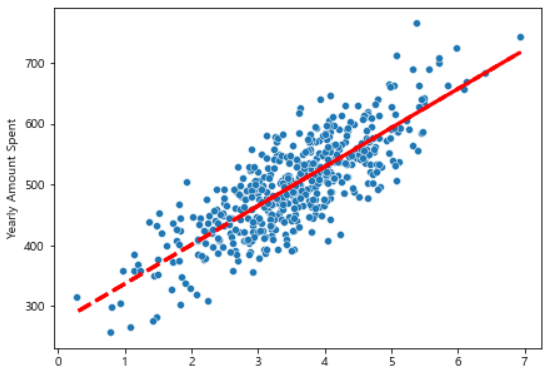
pred = lm.predict(X)

plt.figure(figsize=(7, 5))
sns.scatterplot(x=X[:, 0], y=y)
plt.plot(X[:, 0], pred, 'r', ls='dashed', lw=3)
plt.show()

# 참값 VS 예측값
pred = lm.predict(X)

plt.figure(figsize=(7, 5))
sns.scatterplot(x=y, y=pred)
plt.plot([min(y), max(y)], [min(y), max(y)], 'r', ls='dashed', lw=3)
plt.show()

# 데이터 분리
from sklearn.model_selection import train_test_split
import statsmodels.api as sm

X = data.drop('Yearly Amount Spent', axis=1)
y = data['Yearly Amount Spent']

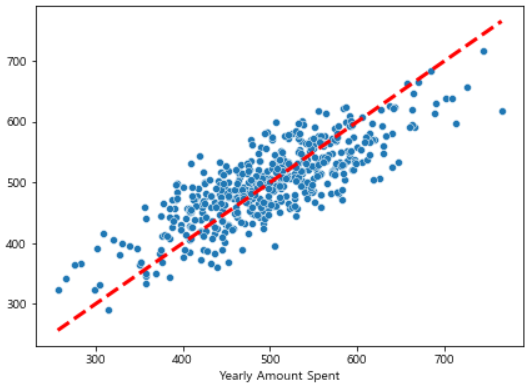
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=13)

# 4개의 컬럼 모두를 변수로 보고 회귀
lm = sm.OLS(y_train, X_train).fit()
lm.summary()

# 참값, 예측값 비교
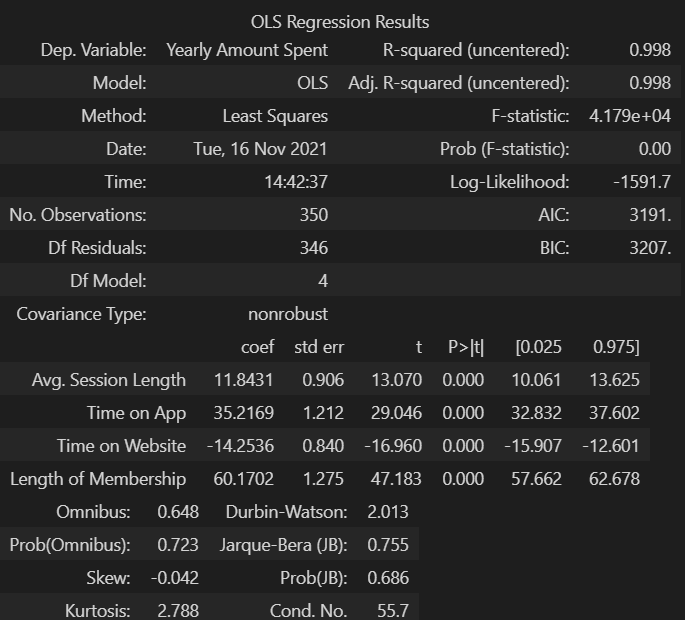
pred = lm.predict(X_test)

plt.figure(figsize=(7, 5))
sns.scatterplot(x=y_test, y=pred)
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], 'r', ls='dashed', lw=3)
plt.show()