알고리즘 - 동적 계획법

✔ 피보나치 수열

◾ 피보나치 수열

• 0항과 1항으로 시작하고 이전의 두 수 합을 다음 항으로 하는 수열
  • 0, 1, 1, 2, 3, 5, 8, 13, ...

◾ 피보나치 수열 함수

• $F0 = 0, F1 = 1$
• $F_i = F_{i-1} + F_{i-2}$ (단, i >= 2)

◾ 재귀 함수 구현

fibo(n){
	if (n < 2) return n;
    else return fibo(n-1) + fibo(n-2);
}

• 문제점 : 숫자가 커지면 중복 호출의 수가 기하급수적으로 증가.
  

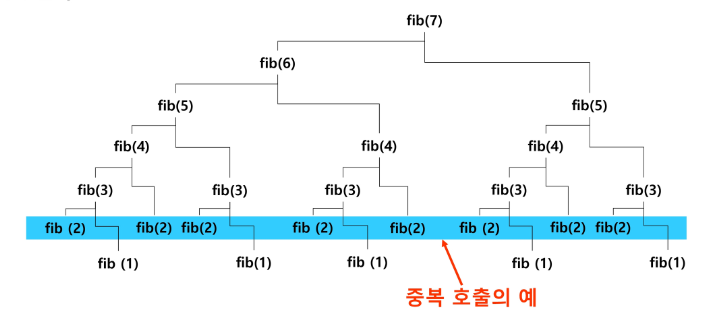
해결 : 메모이제이션

✔ 메모이제이션

◾ 메모이제이션(Memoization)

• 에 계산한 값을 메모리에 저장 매번 다시 계산하지 않도록 하여 전체적인 실행 속도를 빠르게 하는 기술.
• 동적 계획법의 핵심.
• 단점
  • 메모리에 값을 저장하므로 메모리의 낭비가 생김.
  • 재귀 함수 호출로 인한 시스템 호출 스택 사용.
    • 실행 속도 저하 또는 오버플로우 발생 가능.

◾ 메모이제이션 재귀 함수 구현

int[] memo = new int[n];

fibo(n)
if (n >= 2 AND memo[n] = 0)
memo[n] = fibo(n-1) + fibo(n-2)
return memo[n];

---
## ✔ 동적 계획법
#### ◾ 동적 계획법
- **최적화 문제**를 해결하는 알고리즘.
- 동적 계획법 과정
  - 작은 부분 문제들의 해 계산.
  - 이를 이용해 큰 크기의 부분 문제 해결.
  - 최족정으로 원래 주어진 문제를 해결.
- 필요 조건
  - **중복 부분 문제 구조(Overlapping subproblems)**
  - **최적 부분 문제 구조(Optimal substructure)**
#### ◾ 중복 부분 문제 구조
- 작은 문제를 먼저 해결하고 작은 문제들의 최적 해를 이용해 순환적으로 큰 문제 해결.
  - 순환적인 관계(Recurrence Relation) : 일반적으로 점화식으로 표현.
- 순환적인 성질로 이전에 계산한 결과를 저장 공간에 저장.
- 다시 필요한 경우 다시 문제를 재계산하지 않고 저장 공간 확인.
#### ◾ 최적 부분 문제 구조
- **최적화의 원칙(Principle of Optimality)** 을 만족해야만 동적 계획법의 효율적인 적용 가능.
- 최적화의 원칙 : 어떤 문제에 대한 해가 최적일 때 그 해를 구성하는 작은 문제들의 해 역시 최적이어야 한다는 것.
  - 큰 문제의 최적해가 작은 문제들의 최적해로 구성되지 않으면 동적 계획법 사용 불가.
#### ◾ 분할 정복과 동적 계획법
- 분할 정복
  - 연관 없는 부분 문제로 분할
  - 부분 문제를 재귀적으로 해결
  - 부분 문제의 해를 결합(Combine).
  - 예) 병합 정렬, 퀵 정렬
- DP
  - 부분 문제들이 연관이 없으면 적용 불가.
    - 부분 문제들은 더 작은 부분 문제들을 공유.
  - 모든 부분 문제를 한번만 계산하고 결과를 저장하고 재사용.
- 정리
  - DP는 부분 문제들 사이에 의존적 관계 존재.
    - 문제에 따라 다르고 대부분 뚜렷하지 않아 함축적인 순서(Implicit Order)라고 부름.
  - 분할 정복은 하향식 방법, DP는 상향식 방법.
#### ◾ 3단계 DP 적용 방법
- **최적해 구조의 특성 파악**
  - 문제를 부분 문제로 분리.
- **최적해의 값을 재귀적으로 정의**
  - 부분 문제의 최적해 값에 기반하여 문제의 최적해 값 정의.
- **상향식 방법으로 최적해의 값 계산**
  - 가장 작은 부분 문제부터 해를 구한 뒤 테이블에 저장.
  - 테이블에 저장되어 있는 부분 문제의 해를 이용하여 점차적으로 상위 부분 문제의 최적해 계산(상향식 방법)