강의 복습 내용

[DAY 9] Pandas II / 확률론

[AI Math 6강] pandas II

• Groupby
  • SQL groupby 명령어와 같음
  • split -> apply -> combine
  • 과정을 거쳐 연산함
    
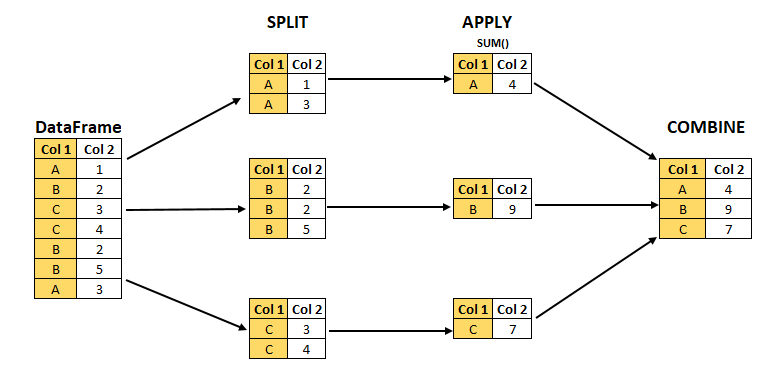
  • 한 개이상의 column을 묶을 수 있음
  • Hierarchical index
    • Groupby 명령의 결과물도 결국은 dataframe
    • 두 개의 column으로 groupby를 할 경우, index가 두개 생성
    • unstack : Group으로 묶여진 데이터를 matrix 형태로 전환해줌
    • swaplevel : Index level을 변경할 수 있음
    • operations : Index level을 기준으로 기본 연산 수행 가능
  • Groupby에 의해 Split된 상태를 추출 가능함
    • Tuple 형태로 그룹의 key값 Value값이 추출됨
    • 특정 key값을 가진 그룹의 정보만 추출 가능
    • 추출된 group 정보에는 세 가지 유형의 apply가 가능함
    • Aggregation : 요약된 통계정보를 추출해 줌
      • 특정 컬럼에 여러개의 function을 Apply 할 수 도 있음
    • Transformation : 해당 정보를 변환해줌
      • Aggregation과 달리 key값 별로 요약된 정보가 아님
      • 개별 데이터의 변환을 지원함
      • 단 max나 min 처럼 Series 데이터에 적용되는 데이터 들은 Key값을 기준으로 Grouped된 데이터 기준
    • Filtration : 특정 정보를 제거 하여 보여주는 필터링 기능
      • 특정 조건으로 데이터를 검색할 때 사용
      • filter안에는 boolean 조건이 존재해야함
      • len(x)는 grouped된 dataframe 개수
• Pivot Table
  • 우리가 excel에서 보던 그 것!
  • Index 축은 groupby와 동일함
  • Column에 추가로 labeling 값을 추가하여,
  • Value에 numeric type 값을 aggregation 하는 형태
• Crosstab
  • 특히 두 칼럼에 교차 빈도, 비율, 덧셈 등을 구할 때 사용
  • Pivot table의 특수한 형태
  • User-Item Rating Matrix 등을 만들 때 사용 가능함
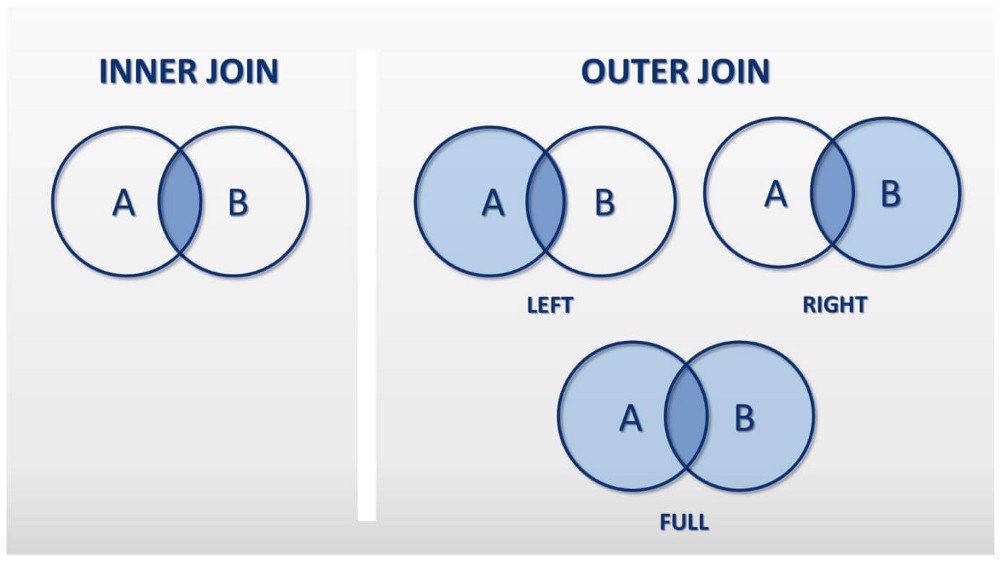
• merge
  • SQL에서 많이 사용하는 Merge와 같은 기능
  • 두 개의 데이터를 하나로 합침
  • join method
    
• concat : 같은 형태의 데이터를 붙이는 연산작업
• Database connection : Data loading시 db connection 기능을 제공함
• XLS persistence
  • Dataframe의 엑셀 추출 코드
  • Xls 엔진으로 openpyxls 또는 XlsxWrite 사용
• Pickle persistence
  • 가장 일반적인 python 파일 persistence
  • to_pickle, read_pickle 함수 사용

[AI Math 6강] 확률론 맛보기

• 딥러닝에서 확률론이 왜 필요한가요?
  • 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있습니다.
  • 기계학습에서 사용되는 손실함수(loss function)들의 작동 원리는 데이터공간을 통계적으로 해석해서 유도하게 됩니다.
  • 회귀 분석에서 손실함수로 사용되는 L2-노름은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도합니다.
  • 분류 문제에서 사용되는 교차엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도합니다.
  • 분산 및 불확실성을 최소화하기 위해서는 측정하는 방법을 알아야 합니다.
• 이산확률변수 vs 연속확률변수
  • 확률변수는 확률분포 𝒟에 따라 이산형(discrete)과 연속형(continuous) 확률변수로 구분하게 됩니다.
  • 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링합니다.
  • 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링합니다.
• 확률분포는 데이터의 초상화
  • 데이터공간을 𝒳×𝒴라 표기하고 𝒟는 데이터공간에서 데이터를 추출하는 분포입니다.
  • 데이터는 확률변수로 (x,y)∼𝒟라 표기합니다.
  • 결합분포 P(x,y)는 𝒟를 모델링합니다.
  • P(x)는 입력 x에 대한 주변확률분포로 y에 대한 정보를 주진 않습니다.
  • 조건부확률분포 P(x|y)는 데이터 공간에서 입력 x와 출력 y 사이의 관계를 모델링합니다.
• 조건부확률과 기계학습
  • 조건부확률 P(y|x)는 입력변수 x에 대해 정답이 y일 확률을 의미합니다.
  • 로지스틱 회귀에서 사용했던 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용됩니다.
  • 분류 문제에서 softmax(Wφ + b)은 데이터 x로부터 추출된 특징패턴 φ(x)과 가중치행렬 W을 통해 조건부확률 P(y|x)을 계산합니다.
  • 회귀 문제의 경우 조건부기대값 𝔼[예|x]을 추정합니다.
  • 딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴 φ을 추출합니다.
• 기대값이 뭔가요?
  • 확률분포가 주어지면 데이터를 분석하는 데 사용 가능한 여러 종류의 통계적 범함수(statistical functional)를 계산할 수 있습니다.
  • 기대값(expectation)은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는데 사용됩니다.
  • 기대값을 이용해 분산, 첨도, 공분산 등 여러 통계량을 계산할 수 있습니다.
• 몬테카를로 샘플링
  • 기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분이다.
  • 확률분포를 모를 때 데이터를 이용하여 기대값을 계산하려면 몬테카를로(Monte Carlo) 샘플링 방법을 사용해야 한다.
  • 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렴성을 보장한다.

Further Question

몬테카를로 방법을 활용하여 원주율에 대한 근사값을 어떻게 구할 수 있을까요?

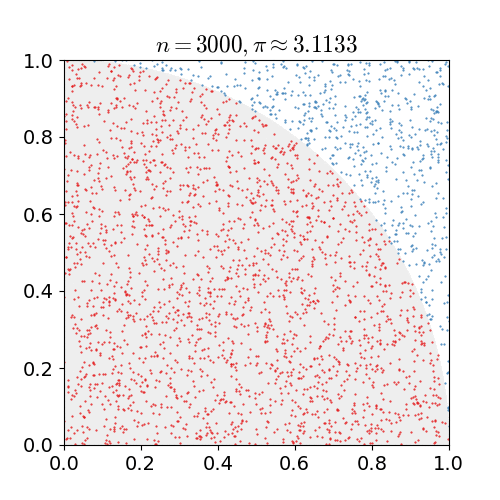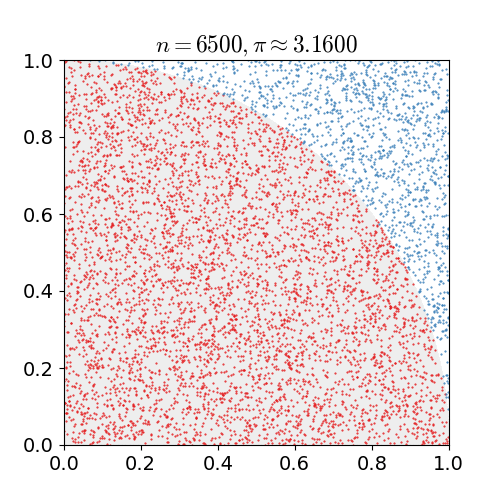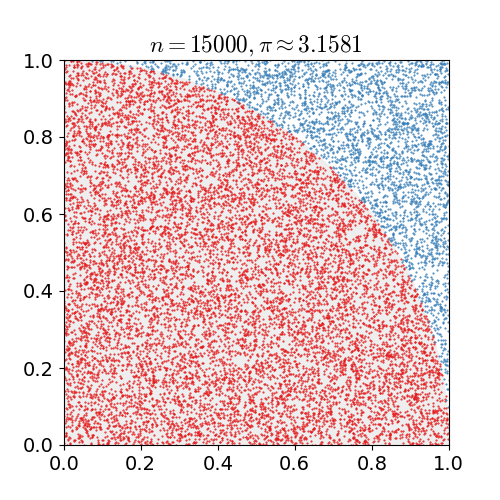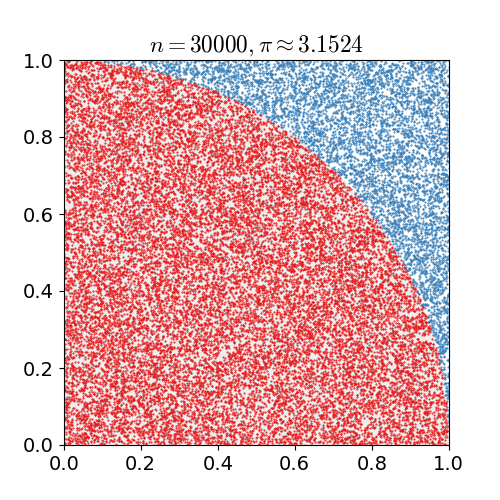
1. 정사각형을 그린 다음, 그 안에 사분면을 삽입합니다.
2. 정사각형 위에 일정한 개수의 점을 균일하게 분포합니다.
3. 사분면 내부의 점(즉, 원점으로부터 1 미만)의 개수를 셉니다.
4. 내부의 개수와 전체 개수의 비율은 두 영역의 비율을 나타냅니다.
5. 사분면 내부의 비율에 4를 곱하여 π를 만듭니다.

여기서 두 가지의 중요한 점이 있습니다.

1. 점이 균일하게 분포되지 않으면 근사치가 떨어집니다.
2. 평균적으로 더 많은 점을 배치할수록 근사치가 개선됩니다.

[개인] 판다스 코드 속도 최적화를 위한 초보자 안내서

판다스 데이터 프레임에 함수를 적용하는 몇 가지 방법론의 효율성을 가장 느린 속도부터 가장 빠른 속도까지 나열하며 검토하겠습니다.

1. 색인을 사용하여 데이터 프레임 행을 반복하는 방법
2. iterrows()를 사용한 반복
3. apply()를 사용한 반복
4. 판다스 시리즈를 사용한 벡터화
5. 넘파이 배열을 사용한 벡터화

판다스에서 단순 반복, 절대 하지 말아야 할 일

• 이 접근법의 장점은 다른 반복 가능한 파이썬 객체와 상호 작용하는 방식, 예컨대 리스트나 튜플에 대해 반복하는 방식과 동일하다는 점입니다.
• 반대로 단점은 판다스의 단순 반복이 아무 짝에 쓸데없는 가장 느린 방법이라는 점입니다.
• 아래에서 논의할 접근법과 달리 판다스의 단순 반복은 내장된 최적화를 이용하지 않기 때문에 극히 비효율적(그리고 종종 읽기도 쉽지 않습니다)입니다.

iterrows()를 사용한 반복

• iterrows()는 데이터 프레임의 행을 반복하며 행 자체를 포함하는 객체에 덧붙여 각 행의 색인을 반환하는 제너레이터입니다.
• iterrows()는 판다스 데이터 프레임과 함께 작동하게끔 최적화되어 있으며 표준 함수 대부분을 실행하는 데 가장 효율적인 방법은 아니지만(나중에 자세히 설명) 단순 반복보다는 상당히 개선되어 있습니다.

apply 메서드를 사용한 더 나은 반복

• apply()는 본질적으로 행을 반복하지만 Cython에서 이터레이터를 사용하는 것 같이 내부 최적화를 다양하게 활용하므로 iterrows()보다 훨씬 효율적입니다.

판다스 시리즈를 사용한 벡터화

• 판다스는 수학 연산에서 집계 및 문자열 함수에 이르기까지 다양한 벡터화 함수를 포함하고 있습니다.
• 내장 함수는 판다스 시리즈와 데이터 프레임에서 작동하게끔 최적화되어있습니다.
• 결과적으로 벡터화 판다스 함수를 사용하는 건 비슷한 목적을 위해 손수 반복시키는 방법보다 거의 항상 바람직합니다.

넘파이 배열을 사용한 벡터화

• 넘파이 라이브러리는 “과학 계산을 위한 파이썬 기본 패키지”를 표방하며 내부가 최적화된, 사전 컴파일된 C 코드로 작업을 수행합니다.
• 판다스와 마찬가지로 넘파이는 배열 객체(ndarrays라고 함) 상에서 작동합니다.
• 그러나 색인, 데이터 유형 확인 등과 같이 판다스 시리즈 작업으로 인한 오버헤드가 많이 발생하지 않습니다.
• 결과적으로 넘파이 배열에 대한 작업은 판다스 시리즈에 대한 작업보다 훨씬 빠릅니다.

결론

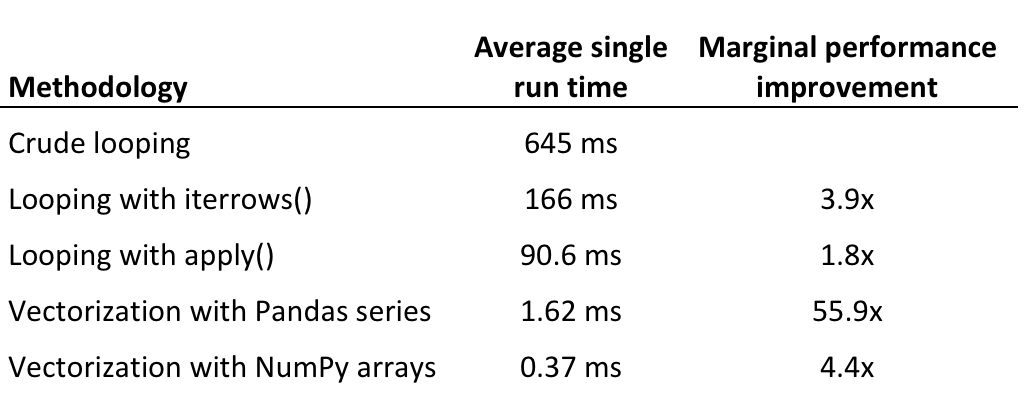
판다스 코드 최적화에 관해 몇 가지 기본적인 결론을 내릴 수 있습니다.

1. 반복을 피해야합니다. 사용 사례 대부분의 경우 반복은 느리고 불필요합니다.
2. 반복해야 하는 경우 반복 함수가 아닌 apply()를 사용해야합니다.
3. 보통은 벡터화가 스칼라 연산보다 낫습니다. 대부분의 판다스 작업은 벡터화시킬 수 있습니다.
4. 넘파이 배열에서의 벡터 연산은 판다스 시리즈에서 수행하는 것보다 효율적입니다.

피어 세션 정리

강의 리뷰 및 Q&A

• [AI Math 6강] pandas II
• [AI Math 6강] 확률론 맛보기

스터디 발표

• 피어 세션 링크 참고

퀴즈 결과 회고

[AI Math 6강 퀴즈] 확률론 맛보기-1~5

1. 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링한다. (O)

ans : 예

2. 연속형 확률변수의 한 지점에서의 밀도 (density)는 그 자체로 확률값을 가진다. (O)

ans : 아니오

3. 몬테카를로 샘플링 방법은 변수 유형 (이산형, 연속형)에 상관없이 사용할 수 있다. (O)

ans : 예

4. 정육면체 주사위의 기대값 계산 (O)

ans : 3.5

5. 정사면체 주사위의 분산 계산 (O)

ans : 5

총평

오늘 강의에서 학습한 몬테카를로 샘플링이 굉장히 인상 깊었습니다.
사실 단순하다면 단순한 방법이지만, 오히려 단순하기 때문에 강력한 방법이라고 생각합니다.
평소 베이지만 통계를 공부해보고 싶다고 생각만 했었는데, 오늘을 시작으로 입문하게 될 것 같습니다.

카카오 아레나에서는 협업 필터링(collaborative filtering)을 기반으로 Base Model을 만들고, 콘텐츠 기반 필터링(content-based filtering)으로 업그레이드하기로 했습니다.
그리고 가능하다면 Base Model은 Deep-Learning으로 할 계획입니다.
구체적인 계획 수립을 위해서 1월 30일 토요일까지 브런치 및 협업 필터링 알고리즘에 대해서 조사해오기로 했습니다.

오늘보다 더 성장한 내일의 저를 기대하며, 내일 뵙도록 하겠습니다.

읽어주셔서 감사합니다!