강의 복습 내용
[Day 24] 정점 표현 & 추천시스템 (심화)
[Graph 7강] 그래프의 정점을 어떻게 벡터로 표현할까?
1. 정점 표현 학습
1.1 정점 표현 학습이란?
- 정점 표현 학습이란 그래프의 정점들을 벡터의 형태로 표현하는 것입니다
- 정점 표현 학습은 간단히 정점 임베딩(Node Embedding)이라고도 부릅니다
- 정점 임베딩은 벡터 형태의 표현 그 자체를 의미하기도 합니다
- 정점이 표현되는 벡터 공간을 임베딩 공간이라고 부릅시다
- 정점 표현 학습의 입력은 그래프입니다
- 주어진 그래프의 각 정점 𝑢에 대한 임베딩, 즉 벡터 표현 𝒛𝑢가 정점 임베딩의 출력입니다
1.2 정점 표현 학습의 이유
- 정점 임베딩의 결과로, 벡터 형태의 데이터를 위한 도구들을 그래프에도 적용할 수 있습니다
- 기계학습 도구들이 한가지 예시입니다
- 대부분 분류기(로지스틱 회귀분석, 다층 퍼셉트론 등) 그리고 군집 분석 알고리즘(K-Means, DBSCAN 등)은 벡터 형태로 표현된 사례(Instance)들을 입력으로 받습니다
- 그래프의 정점들을 벡터 형태로 표현할 수 있다면, 위의 예시와 같은 대표적인 도구들 뿐 아니라, 최신의 기계 학습도구들을 정점 분류(Node Classification), 군집 분석(Community Detection) 등에 활용할 수 있습니다
1.3 정점 표현 학습의 목표
- 어떤 기준으로 정점을 벡터로 변환해야할까요?
- 그래프에서의 정점간 유사도를 임베딩 공간에서도 “보존”하는 것을 목표로 합니다
- 임베딩 공간에서의 𝑢와 𝑣의 유사도는 둘의 임베딩의 내적 𝒛𝑣⊺𝒛𝑢 = ||𝒛𝑢||⋅||𝒛𝑣||⋅𝒄𝒐𝒔(𝜽)입니다
- 내적은 두 벡터가 클 수록, 그리고 같은 방향을 향할 수록 큰 값을 갖습니다
- 그래프에서 두 정점의 유사도는 어떻게 정의할까요?
- 이 질문에는 여러가지 답이 있을 수 있습니다
- 본 강의에서는 대표적인 답을 몇 가지를 설명합니다
- 정리하면, 정점 임베딩은 다음 두 단계로 이루어집니다
1) 그래프에서의 정점 유사도를 정의하는 단계
2) 정의한 유사도를 보존하도록 정점 임베딩을 학습하는 단계
2. 인접성 기반 접근법
2.1 인접성 기반 접근법
- 인접성(Adjacency) 기반 접근법에서는 두 정점이 인접할 때 유사하다고 간주합니다
- 두 정점 𝑢와 𝑣가 인접하다는 것은 둘을 직접 연결하는 간선 (𝑢,𝑣)가 있음을 의미합니다
- 인접행렬(Adjacency Matrix) 𝐀의 𝑢행 𝑣열 원소 𝐀𝑢,𝑣는 𝑢와 𝑣가 인접한 경우 1아닌 경우 0입니다
- 인접행렬의 원소 𝐀𝑢,𝑣 를 두 정점 𝑢와 𝑣의 유사도로 가정합니다
- 인접성 기반 접근법의 손실 함수(Loss Function)는 아래와 같습니다
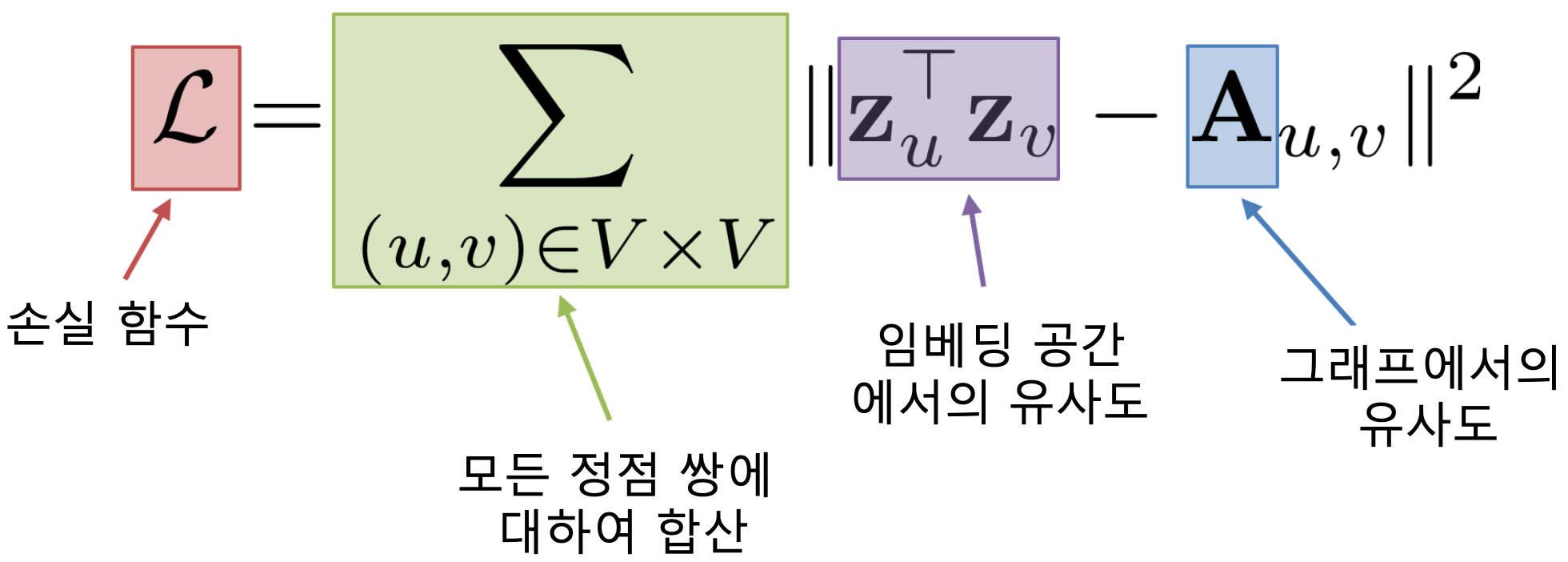
- 즉, 이 손실 함수가 최소가 되는 정점 임베딩을 찾는 것을 목표로 합니다
- 손실 함수 최소화를 위해서는 (확률적) 경사하강법 등이 사용됩니다
2.2 인접성 기반 접근법의 한계
- 인접성만으로 유사도를 판단하는 것은 한계가 있습니다
- 빨간색 정점과 파란색 정점은 거리가 3인 반면 초록색 정점과 파란색 정점은 거리가 2입니다
- 인접성만을 고려할 경우 이러한 사실에 대한 고려 없이, 두 경우의 유사도는 0으로 같습니다
- 인접성만으로 유사도를 판단하는 것은 한계가 있습니다
- 군집 관점에서는 빨간색 정점과 파란색 정점은 다른 군집에 속하는 반면 초록색 정점과 파란색 정점은 다른 군집에 속합니다
- 인접성만을 고려할 경우 이러한 사실에 대한 고려 없이, 두 경우의 유사도는 0으로 같습니다
3. 거리/경로/중첩 기반 접근법
3.1 거리 기반 접근법
- 거리 기반 접근법에서는 두 정점 사이의 거리가 충분히 가까운 경우 유사하다고 간주합니다
3.2 경로 기반 접근법
- 경로 기반 접근법에서는 두 정점 사이의 경로가 많을 수록 유사하다고 간주합니다
- 정점 𝑢와 𝑣의 사이의 경로(Path)는 아래 조건을 만족하는 정점들의 순열(Sequence)입니다
(1) 𝑢에서 시작해서 𝑣에서 끝나야 합니다
(2) 순열에서 연속된 정점은 간선으로 연결되어 있어야 합니다 - 두 정점 𝑢와 𝑣의 사이의 경로 중 거리가 𝑘인 것은 수는 𝐀𝑢,𝑣^𝑘와 같습니다
- 즉, 인접 행렬 𝐀의 𝑘 제곱의 𝑢행 𝑣열 원소와 같습니다
- 경로 기반 접근법의 손실 함수는 다음과 같습니다
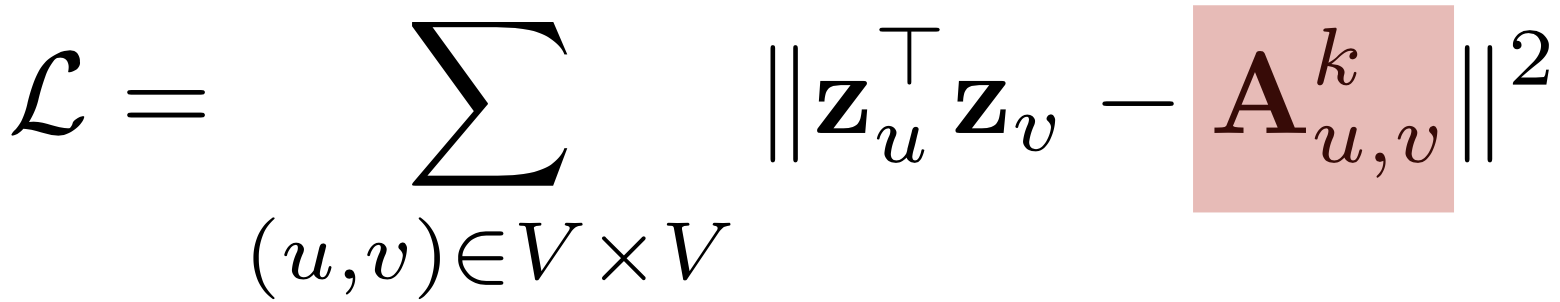
3.3 중첩 기반 접근법
- 중첩 기반 접근법에서는 두 정점이 많은 이웃을 공유할 수록 유사하다고 간주합니다
- 정점 𝑢의 이웃 집합을 𝑁(𝑢) 그리고 정점 𝑣의 이웃 집합을 𝑁(𝑣)라고 하면 두 정점의 공통 이웃 수 𝑆𝑢,𝑣는 다음과 같이 정의 됩니다
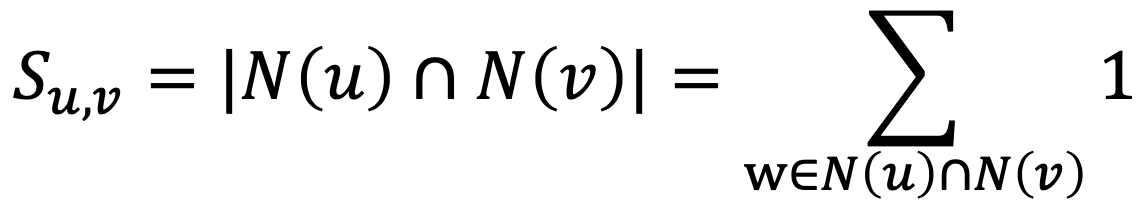
- 중첩 기반 접근법의 손실 함수는 다음과 같습니다
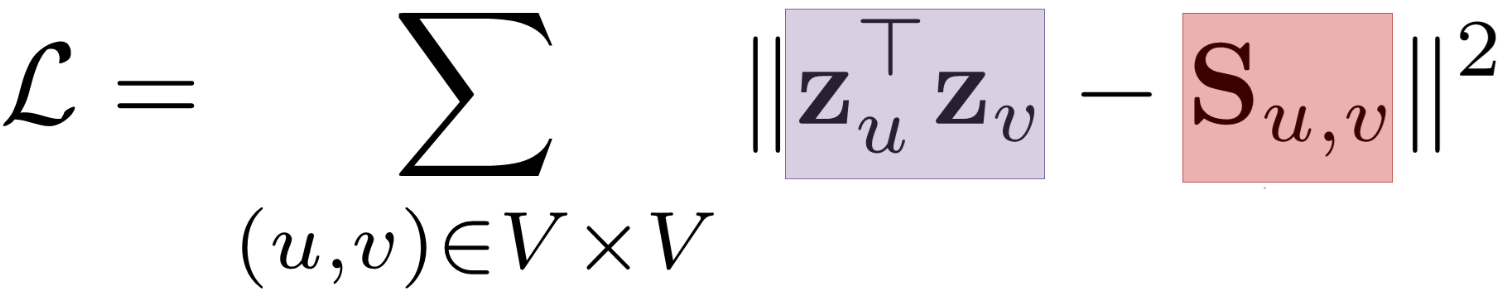
- 공통 이웃 수를 대신 자카드 유사도 혹은 Adamic Adar 점수를 사용할 수도 있습니다
- 자카드 유사도(Jaccard Similarity)는 공통 이웃의 수 대신 비율을 계산하는 방식입니다
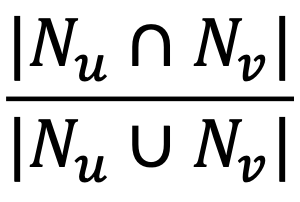
- Adamic Adar 점수는 공통 이웃 각각에 가중치를 부여하여 가중합을 계산하는 방식입니다
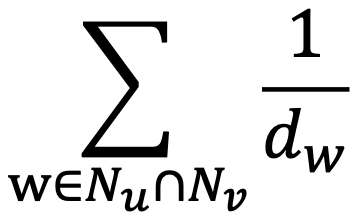
4. 임의보행 기반 접근법
- 임의보행 기반 접근법에서는 한 정점에서 시작하여 임의보행을 할 때 다른 정점에 도달할 확률을 유사도로 간주합니다
- 임의보행이란 현재 정점의 이웃 중 하나를 균일한 확률로 선택하는 이동하는 과정을 반복하는 것을 의미합니다
- 임의보행을 사용할 경우 시작 정점 주변의 지역적 정보와 그래프 전역 정보를 모두 고려한다는 장점이 있습니다
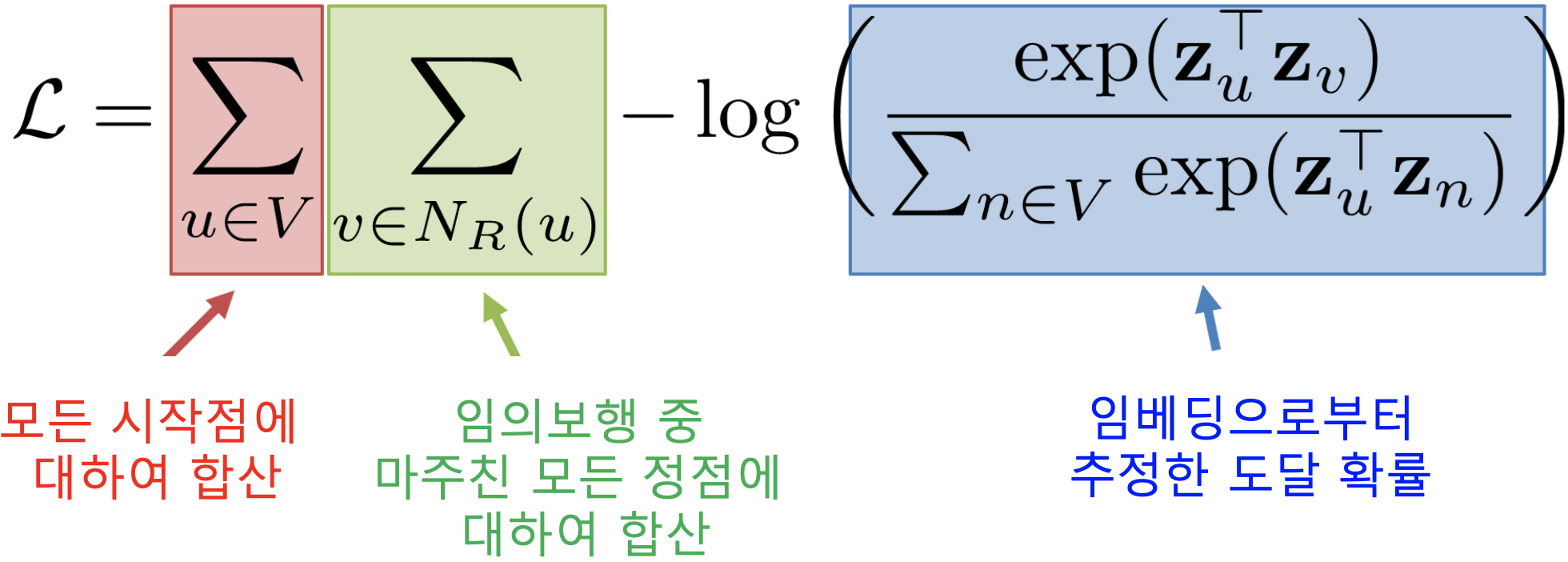
- 임의보행 기반 접근법은 세 단계를 거칩니다
1) 각 정점에서 시작하여 임의보행을 반복 수행합니다
2) 각 정점에서 시작한 임의보행 중 도달한 정점들의 리스트를 구성합니다. 이 때, 정점 𝑢에서 시작한 임의보행 중 도달한 정점들의 리스트를 𝑁𝑅(𝑢)라고 합시다. 한 정점을 여러 번 도달한 경우, 해당 정점은 𝑁𝑅(𝑢)에 여러 번 포함될 수 있습니다
3) 다음 손실함수를 최소화하는 임베딩을 학습합니다

- 어떻게 임베딩으로부터 도달 확률을 추정할까요?
- 정점 𝑢에서 시작한 임의보행이 정점 𝑣에 도달할 확률 𝑃(𝑣|𝑧𝑢)을 다음과 같이 추정합니다

- 즉 유사도 𝒛𝑣⊺𝒛𝑢가 높을 수록 도달 확률이 높습니다
- 추정한 도달 확률을 사용하여 손실함수를 완성하고 이를 최소화하는 임베딩을 학습합니다
4.2 DeepWalk와 Node2Vec
- 임의보행의 방법에 따라 DeepWalk와 Node2Vec이 구분됩니다
- DeepWalk는 앞서 설명한 기본적인 임의보행을 사용합니다
- 즉, 현재 정점의 이웃 중 하나를 균일한 확률로 선택하는 이동하는 과정을 반복합니다
- Node2Vec은 2차 치우친 임의보행(Second-order Biased Random Walk)을 사용합니다
- 현재 정점(예시에서 𝑣)과 직전에 머물렀던 정점(예시에서 𝑢)을 모두 고려하여 다음 정점을 선택합니다
- 직전 정점의 거리를 기준으로 경우를 구분하여 차등적인 확률을 부여합니다
- Node2Vec에서는 부여하는 확률에 따라서 다른 종류의 임베딩을 얻습니다
- 멀어지는 방향에 높은 확률을 부여한 경우, 정점의 역할(다리 역할, 변두리 정점 등)이 같은 경우 임베딩이 유사합니다
- 가까워지는 방향에 높은 확률을 부여한 경우, 같은 군집(Community)에 속한 경우 임베딩이 유사합니다
4.3 손실 함수 근사
- 임의보행 기법의 손실함수는 계산에 정점의 수의 제곱에 비례하는 시간이 소요됩니다
- 중첩된 합 때문입니다
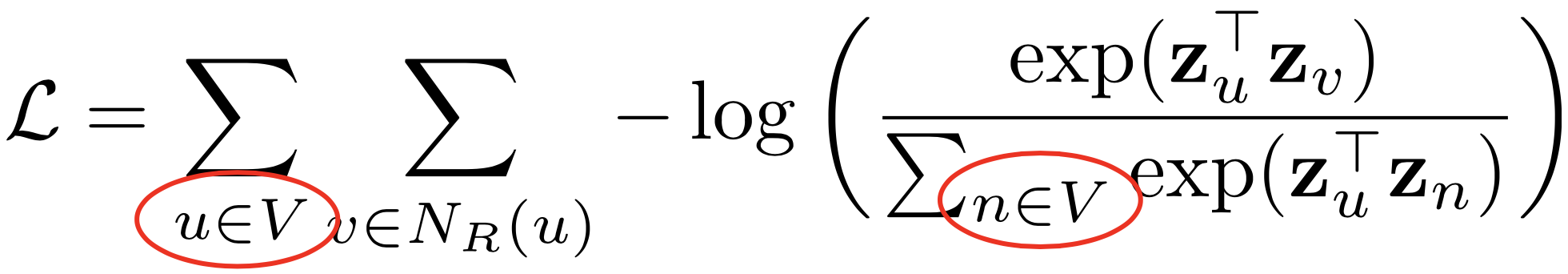
- 정점이 많은 경우, 제곱은 매우 큰 숫자입니다
- 따라서 많은 경우 근사식을 사용합니다
- 모든 정점에 대해서 정규화하는 대신 몇 개의 정점을 뽑아서 비교하는 형태입니다
- 이 때 뽑힌 정점들을 네거티브 샘플이라고 부릅니다
- 연결성에 비례하는 확률로 네거티브 샘플을 뽑으며, 네거티브 샘플이 많을 수록 학습이 더욱 안정적입니다
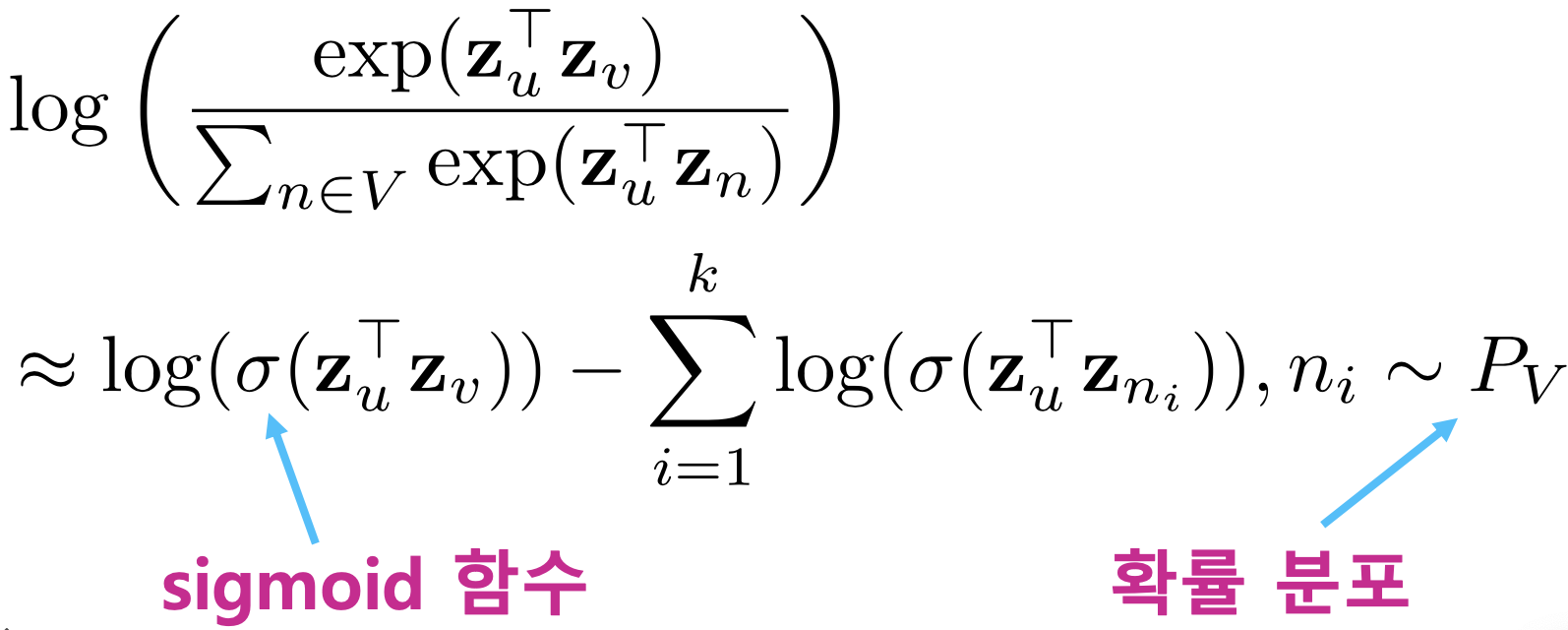
5. 변환식 정점 표현 학습의 한계
5.1 변환식 정점 표현 학습과 귀납식 정점 표현 학습
- 지금까지 소개한 정점 임베딩 방법들을 변환식(Transductive) 방법입니다
- 변환식(Transdctive) 방법은 학습의 결과로 정점의 임베딩 자체를 얻는다는 특성이 있습니다
- 정점을 임베딩으로 변화시키는 함수, 즉 인코더를 얻는 귀납식(Inductive) 방법과 대조됩니다
5.2 변환식 정점 표현 학습의 한계
- 변환식 임베딩 방법은 여러 한계를 갖습니다
1) 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩을 얻을 수 없습니다
2) 모든 정점에 대한 임베딩을 미리 계산하여 저장해두어야 합니다
3) 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 없습니다 - 대표적인 귀납식 임베딩 방법이 바로 그래프 신경망(Graph Neural Network)입니다
7강 정리
- 정점 표현 학습
- 그래프의 정점들을 벡터로 표현하는 것
- 그래프에서 정점 사이의 유사성을 계산하는 방법에 따라 여러 접근법이 구분됨
- 인접성 기반 접근법
- 거리/경로/중첩 기반 접근법
- 임의보행 기반 접근법
- 임의보행 방법에 따라 DeepWalk와 Node2Vec가 구분됨
- 변환식 정점 표현 학습의 한계
[Graph 8강] 그래프를 추천시스템에 어떻게 활용할까? (심화)
1. 추천시스템 기본 복습
1.1 추천 시스템 예시
- Amazon.com (상품), 넷플릭스 (영화), 유튜브 (영상), 페이스북 (친구)
1.2 추천 시스템과 그래프
- 추천 시스템은 사용자 각각이 구매할 만한 혹은 선호할 만한 상품/영화/영상을 추천합니다
- 추천 시스템의 핵심은 사용자별 구매를 예측하거나 선호를 추정하는 것입니다
- 그래프 관점에서 추천 시스템은 “미래의 간선을 예측하는 문제” 혹은 “누락된 간선의 가중치를 추정하는 문제”로 해석할 수 있습니다
1.3 내용 기반 추천시스템
- 내용 기반 추천은 각 사용자가 구매/만족했던 상품과 유사한 것을 추천하는 방법입니다
- 내용 기반 추천시스템은 다음 장/단점을 같습니다
(+) 다른 사용자의 구매 기록이 필요하지 않습니다
(+) 독특한 취향의 사용자에게도 추천이 가능합니다
(+) 새 상품에 대해서도 추천이 가능합니다
(+) 추천의 이유를 제공할 수 있습니다
(-) 상품에 대한 부가 정보가 없는 경우에는 사용할 수 없습니다
(-) 구매 기록이 없는 사용자에게는 사용할 수 없습니다
(-) 과적합(Overfitting)으로 지나치게 협소한 추천을 할 위험이 있습니다
1.4 협업 필터링
- 협업 필터링은 유사한 취향의 사용자들이 선호/구매한 상품을 추천하는 방법입니다
- 협업 필터링은 다음의 장/단점을 갖습니다
(+) 상품에 대한 부가 정보가 없는 경우에도 사용할 수 있습니다
(−) 충분한 수의 평점 데이터가 누적되어야 효과적입니다
(−) 새 상품, 새로운 사용자에 대한 추천이 불가능합니다
(−) 독특한 취향의 사용자에게 추천이 어렵습니다
1.5 추천시스템의 평가
- 훈련 데이터를 이용하여 추정한 점수를 평가 데이터와 비교하여 정확도를 측정합니다
- 오차를 측정하는 지표로는 평균 제곱 오차(Mean Squared Error, MSE)가 많이 사용됩니다 평가 데이터 내의 평점들을 집합을 𝑇라고 합시다
- 평균 제곱급 오차(Root Mean Squared Error, RMSE)도 많이 사용됩니다
2. 넷플릭스 챌린지 소개
2.1 넷플릭스 챌린지 데이터셋
- 넷플릭스 챌린지(Netflix Challenge)에서는 사용자별 영화 평점 데이터가 사용되었습니다
- 훈련 데이터(Training Data)는 2000년부터 2005년까지 수집한
- 48만명 사용자의 1만 8천개의 영화에 대한 1억 개의 평점으로 구성되어 있습니다
- 평가 데이터(Test Data)는 각 사용자의 최신 평점 280만개로 구성되어 있습니다
2.2 넷플릭스 챌린지 대회 소개
- 넷플릭스 챌린지의 목표는 추천시스템의 성능을 10%이상 향상시키는 것이었습니다
- 평균 제곱근 오차 0.9514을 0.8563까지 낮출 경우 100만불의 상금을 받는 조건이었습니다
- 2006년부터 2009년까지 진행되었으며, 2700개의 팀이 참여하였습니다
- 넷플릭스 챌린지를 통해 추천시스템의 성능이 비약적으로 발전했습니다
3. 잠재 인수 모형
3.1 잠재 인수 모형 개요
- 잠재 인수 모형(Latent Factor Model)의 핵심은 사용자와 상품을 벡터로 표현하는 것입니다
- 잠재 인수 모형에서는 고정된 인수 대신 효과적인 인수를 학습하는 것을 목표로 합니다
- 학습한 인수를 잠재 인수(Latent Factor)라 부릅니다
3.2 손실 함수
- 사용자와 상품을 임베딩하는 기준은 무엇인가요?
- 사용자와 상품의 임베딩의 내적(Inner Product)이 평점과 최대한 유사하도록 하는 것입니다
- 사용자 𝑥의 임베딩을 𝑝𝑥, 상품 𝑖의 임베딩을 𝑞𝑖라고 합시다
- 사용자 𝑥의 상품 𝑖에 대한 평점을 𝑟𝑥𝑖라고 합시다
- 임베딩의 목표는 𝑝𝑥⊺𝑞𝑖이 𝑟𝑥𝑖와 유사하도록 하는 것입니다
- 사용자 수의 열과 상품 수의 행을 가진 평점 행렬을 𝑅이라고 합시다
- 사용자들의 임베딩, 즉 벡터를 쌓아서 만든 사용자 행렬을 𝑃라고 합시다
- 영화들의 임베딩, 즉 벡터를 쌓아서 만든 상품 행렬을 𝑄라고 합시다
- 잠재 인수 모형은 다음 손실 함수를 최소화하는 𝑃와 𝑄를 찾는 것을 목표로 합니다

- 하지만, 위 손실 함수를 사용할 경우 과적합(Overfitting)이 발생할 수 있습니다
- 과적합이란 기계학습 모형이 훈련 데이터의 잡음(Noise)까지 학습하여, 평가 성능은 오히려 감소하는 현상을 의미합니다
- 과적합을 방지하기 위하여 정규화 항을 손실 함수에 더해줍니다

- 정규화는 극단적인, 즉 절댓값이 너무 큰 임베딩을 방지하는 효과가 있습니다
3.3 최적화
- 손실함수를 최소화하는 𝑃와 𝑄를 찾기 위해서는 (확률적) 경사하강법을 사용합니다
- 경사하강법은 손실함수를 안정적으로 하지만 느리게 감소시킵니다
- 확률적 경사하강법은 손실함수를 불안정하지만 빠르게 감소시킵니다
- 실제로는 확률적 경사하강법이 더 많이 사용됩니다
4. 고급 잠재 인수 모형
4.1 사용자와 상품의 편향을 고려한 잠재 인수 모형
- 각 사용자의 편향은 해당 사용자의 평점 평균과 전체 평점 평균의 차입니다
- 개선된 잠재 인수 모형에서는 평점을 전체 평균, 사용자 편향, 상품 편향, 상호작용으로 분리합니다
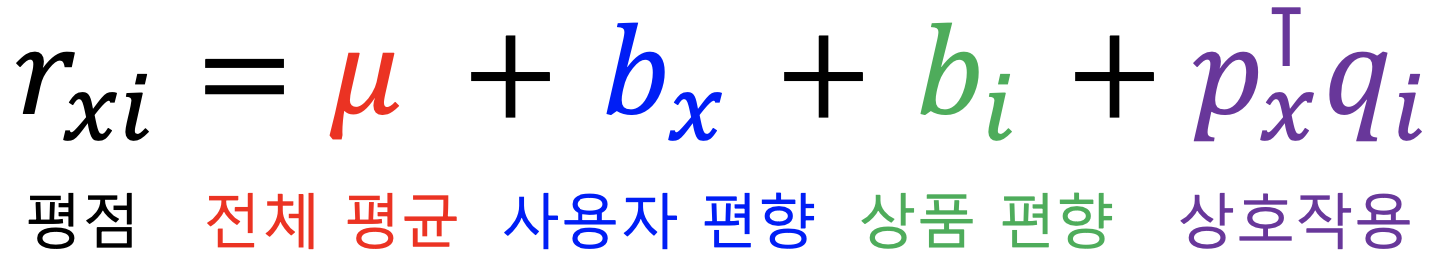
- 개선된 잠재 인수 모형의 손실 함수는 아래와 같습니다
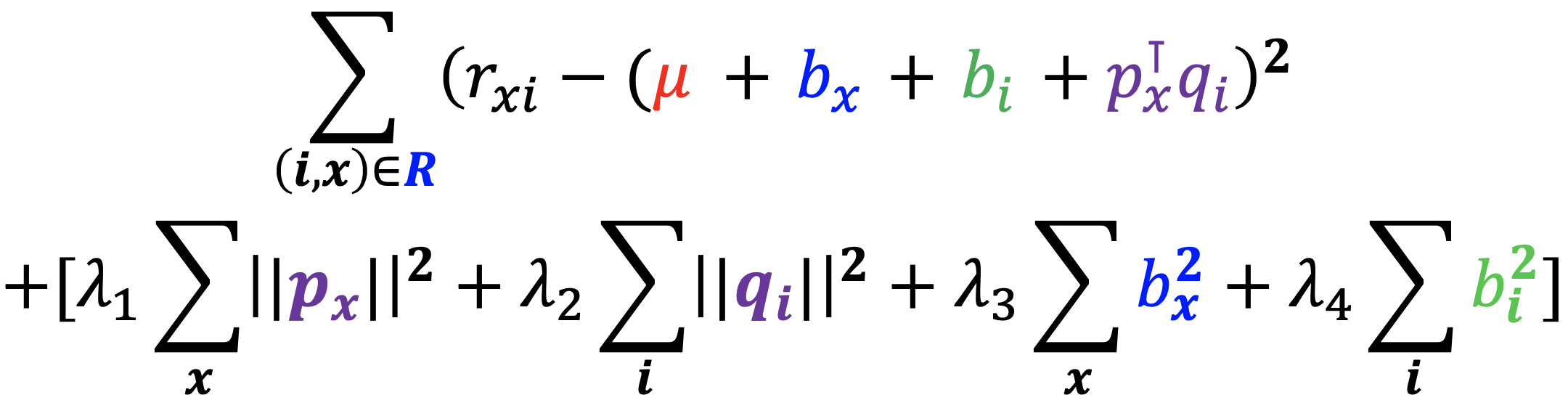
- (확률적) 경사하강법을 통해 손실 함수를 최소화하는 잠재 인수와 편향을 찾아냅니다
4.2 시간적 편향을 고려한 잠재 인수 모형
- 넷플릭스 시스템의 변화로 평균 평점이 크게 상승하는 사건이 있었습니다
- 영화의 평점은 출시일 이후 시간이 지남에 따라 상승하는 경향을 갖습니다
- 개선된 잠재 인수 모형에서는 이러한 시간적 편향을 고려합니다
- 구체적으로 사용자 편향과 상품 편향을 시간에 따른 함수로 가정합니다

5. 넷플릭스 챌린지의 결과
5.1 앙상블 학습
- BellKor 팀은 앙상블 학습을 사용하여 처음으로 목표 성능에 도달하였습니다
- BellKor 팀의 독주에 위기감을 느낀 다른 팀들은 연합팀 Ensemble을 만들었습니다
- 그 결과 Ensemble 팀 역시 목표 성능에 도달하였습니다
5.2. 넷플릭스 챌린지의 우승팀
- 넷플릭스 챌린지 종료 시점에 BellKor 팀 Ensemble 팀의 오차는 정확히 동일했습니다
- 하지만 BellKor 팀의 제출이 20분 빨랐습니다.
- BellKor 팀의 우승입니다!
8강 정리
- 추천시스템 기본 복습
- 내용 기반 추천, 협업 필터링 등
- 넷플릭스 챌린지 소개
- 기본 잠재 인수 모형
- 사용자 임베딩, 상품 임베딩을 학습
- 임베딩의 내적으로 평점을 근사
- 고급 잠재 인수 모형
- 사용자 편향, 상품 편향, 시간적 편향을 고려
- 넷플릭스 챌린지의 결과
Further Question
추천시스템의 성능을 측정하는 metric이 RMSE라는 것은 예상 평점이 높은 상품과 낮은 상품에 동일한 페널티를 부여한다는 것을 뜻합니다. 하지만 실제로 추천시스템에서는 내가 좋아할 것 같은 상품을 추천해주는것, 즉 예상 평점이 높은 상품을 잘 맞추는것이 중요합니다. 이를 고려하여 성능을 측정하기 위해서는 어떻게 해야 할까요?
- Normalized Discounted Cumulative Gain
- Cumulative Gain (CG)
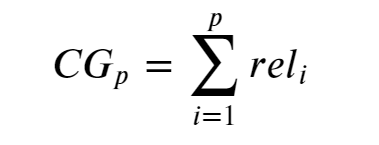
- Discounted Cumulateive Gain (DCG)
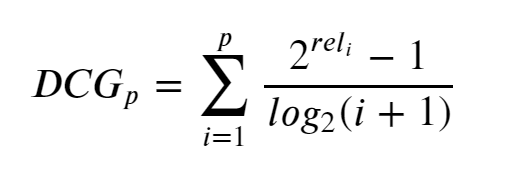
- Normalized Discounted Cumulative Gain (nDCG)
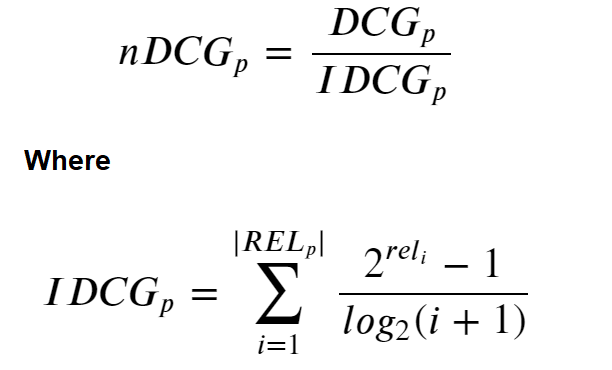
- Cumulative Gain (CG)
추천 시스템의 성능을 향상시키기 위해서는 어떠한 것을 더 고려할 수 있을까요? (해당 문제는 정답이 제공되지 않는 문제입니다. 자유롭게 여러분의 의견을 이야기해보세요.)
- 시계열을 고려한 추천 시스템
피어 세션 정리
강의 리뷰 및 Q&A
- [Graph 7강] 그래프의 정점을 어떻게 벡터로 표현할까?
- [Graph 8강] 그래프를 추천시스템에 어떻게 활용할까? (심화)
[개인] Netflix Prize
- NETFLIX PRIZE – 다이나믹 했던 알고리즘 대회 (1)
- NETFLIX PRIZE – 다이나믹 했던 알고리즘 대회 (2)
- NETFLIX PRIZE – 다이나믹 했던 알고리즘 대회 (3)
총평
강의에서 소개해준 Netflix Prize의 이야기가 흥미진진하길래, 개인적으로 찾아보니 한 편의 영화를 본 것만 같아서 재미있었습니다.
그리고 Futher Question을 통해 추천시스템의 성능을 측정할 때 RMSE를 왜 사용하면 안 되는지에 대해서 생각해볼 수 있었습니다.
이와 관련하여, 카카오 아레나의 브런치 사용자를 위한 글 추천 대회에서 사용되는 Metric인 Normalized Discounted Cumulative Gain과 Mean Average Precision 그리고 Entropy Diversity에 대해서 다시 공부해 보았습니다.
예전에는 왜 이렇게 복잡한 Metric을 사용하는지 몰랐었는데, 오늘처럼 이유를 알고 나니 해당 Metric들을 조금 더 깊이 있게 이해할 수 있었습니다.
오늘보다 더 성장한 내일의 저를 기대하며, 내일 뵙도록 하겠습니다.
읽어주셔서 감사합니다!
