알고리즘 복잡도 계산 항목
1. 시간 복잡도: 알고리즘 실행 속도
2. 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈
시간이 중요하다.
알고리즘 최악의 실행 시간을 표기한다. (최소 이 성능을 보장한다는 의미)
시간 복잡도 계산은 반복문의 영향이 크다.
입력 n에 따라 몇번 계산이 실행되는지를 표현식에 가장 큰 영향을 미치는 n의 단위로 표기한다.
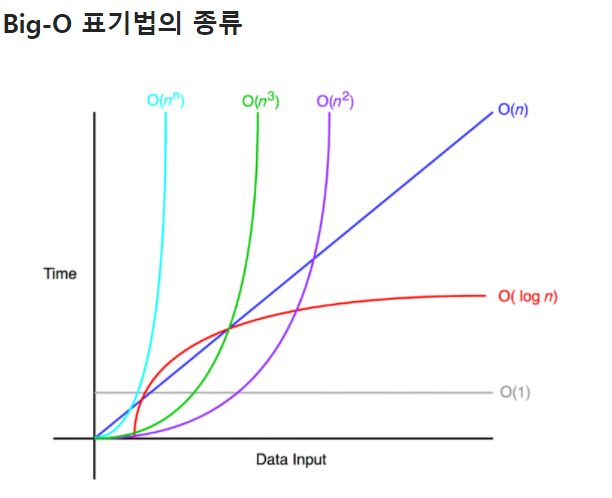
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(2ⁿ)
시간의 하한(가장 느린), 시간의 상한(가장 빠른)
정렬방법과 빅오표기법
과거 작성해둔 자바스크립트 정렬 구현: https://blog.naver.com/namju1v/222226455895
선형 검색: O(n)
원하는 원소가 발견될 때까지 처음부터 마지막 자료까지 차례대로 검색
선형 검색 알고리즘은 정확하지만 아주 효율적이지 못한 방법
선형 검색은 자료가 정렬되어 있지 않거나 그 어떤 정보도 없어 하나씩 찾아야 하는 경우에 유용
최상의 경우 1회로 검색 가능
이진 탐색: O(logn)
만약 배열이 정렬되어 있다면, 배열 중간 인덱스부터 시작하여 찾고자 하는 값과 비교하며 그보다 작은(작은 값이 저장되어 있는) 인덱스 또는 큰 (큰 값이 저장되어 있는) 인덱스로 이동을 반복
최상의 경우 1 (가운데 수가 찾고자 하는 수)
버블 정렬: O(n²)
두 개의 인접한 자료 값을 비교하면서 위치를 교환하는 방식
버블 정렬은 단 두 개의 요소만 정렬해주는 좁은 범위의 정렬에 집중.
이 접근법은 간단하지만 단 하나의 요소를 정렬하기 위해 너무 많이 교환하는 낭비가 발생.
정렬이 되어 있는지 여부에 관계 없이 루프를 돌며 비교한다.(상한/하한 모두 n²)
(교환이 일어나지 않을때 중단한다는 조건이 있으면 가장 최상의 경우 n번)
Repeat n–1 times
For i from 0 to n–2
If i'th and i+1'th elements out of order
Swap them선택 정렬: O(n²)
열 안의 자료 중 가장 작은 수(혹은 가장 큰 수)를 찾아 첫 번째 위치(혹은 가장 마지막 위치)의 수와 교환해주는 방식의 정렬입니다. 선택 정렬은 교환 횟수를 최소화하는 반면 각 자료를 비교하는 횟수는 증가합니다. 정렬되어있어도 n²번 체크한다.
For i from 0 to n–1
Find smallest item between i'th item and last item
Swap smallest item with i'th item
병합 정렬: O(nlogn)
병합 정렬은 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가며 정렬을 하는 방식
그리고 이 과정은 재귀적으로 구현됨.
병합 정렬 실행 시간의 상한은 O(n log n) 입니다.
숫자들을 반으로 나누는 데는 O(log n)의 시간이 들고, 각 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)의 시간이 걸리기 때문. 실행 시간의 하한도 역시 Ω(n log n) 입니다. 숫자들이 이미 정렬되었는지 여부에 관계 없이 나누고 병합하는 과정이 필요하기 때문입니다.
삽입 정렬: O(n²)
가장 처음부터 자기 자신까지 포함해 정렬을 실행, 자기 자신을 제외하고는 이미 정렬되어있는 상태라고 가정한다.
원소의 끝까지 처음 원소부터 끝 원소까지 정렬을 실행한다.
이미 정렬되어있는 상태라면 O(n)이 될 수 있다.
퀵 정렬: O(nlogn)
임의의 값을 기준으로 작은 값과 큰 값으로 분할한다.
이 과정을 작은 값 부분에서, 큰 값 부분에서 반복적으로 실행해 제일 작은 단위로 정렬 될 때까지 실행한다.
결국에는 n개 원소에 대해 모두 분할하는 작업이 요구되므로 O(n)복잡도,
그러나 분할을 반복할 대상이 반으로 규모가 줄어드므로 O(log n)을 대상으로 실행하게 된다.
즉 O(nlog n)복잡도를 갖는다.
최악의 경우에는 O(n²)복잡도를 갖는데 이는 임의로 뽑은 수가 원소 중 가장 작은 값이거나 큰 값일 때 불균형 적으로 원소들이 반으로 나누어지는 상황이다. 분할하는 횟수 n은 동일한데, 비교대상은 n-1, n-2정도로 줄어들어 결국 n에 대하여 n번 분할이 발생하므로 O(n²)이다.
