> 해시테이블
: 배열과 연결리스트를 조합한 것,
배열의 특성을 갖고있어 값들을 순환하지 않고, 고유 인덱스(키)에 접근해 빠른 검색 속도를 갖는다. O(1)
- key에 데이터(value)를 저장하는 데이터 구조이다.
- 해쉬 Hash : 임의 값을 고정 길이로 변환(배열)
해쉬 함수: 해쉬 슬롯마다 고유한 키값(Hash code)를 주기 위해 특별한 알고리즘이 사용된다. 같은 입력값에 대해서는 같은 출력값을 보장한다. 또한, 해쉬코드를 기반으로 해쉬함수의 최초값(인자)를 파악할 수 없다. (양방향x, 일방향성을 갖는다.)
(정수값을 반환하며 해쉬코드 자체가 배열의 인덱스로 여겨진다. 주솟값, 해쉬값이 저장되어있는 한 공간은 슬롯이라고 하고 일반적으로 고유한 코드를 부여하지만,
1) 만일 해쉬함수에 문제가 있는 경우 키값이 중복되는 문제가 생길수 있다.
2) 배열을 우선 선언하고 해쉬코드가 부여되는데 코드가 달라도 한정된 배열공간일 때 저장 공간이 중복된다. -> 단점_collison )
> 사용되는 경우
- 무결성이 요구되는 경우
- 캐쉬 구현시 (중복 확인이 쉽기 때문)
- 블록 체인
- Git
- 동일한 파일 식별 및 검출 (유튜브)
> 장점과 단점
- 장점:
- 데이터의 검색 속도가 빠르다.
- 키에 대한 데이터 유무확인이 쉽다. (중복체크)
- 단점:
- 고유데이터를 저장하기 위해 저장공간이 더 많이 필요하다.
- 완전하지 않다. 키에 해당하는 주소가 동일하게 hashing(hash함수로 계산됨을 의미)된 경우 충돌이 발생하며, 동일 공간에 저장할 수 없어 이를 해결한 다른 자료구조가 요구된다. (해쉬 충돌_Hash Collison이라고 한다.)
- 충돌이 많아질 수록 시간복잡도가 O(1)->O(n)에 가까워진다. 이를 해결하기 위해서는 중복되는 해쉬가 있다면 데이터를 새로 저장할 슬롯을 찾은 뒤에 저장할 수 있다.
> 해쉬충돌 해결하기
- 충돌이 빈번할 경우
: 해쉬 함수를 재정의하거나 해쉬테이블을 확대.
: hash function를 무조건 1:1 로 만드는 것보다 Collision 을 최소화하는 방향으로 설계하고 발생하는 Collision 에 대비해 어떻게 대응할 것인가가 더 중요하다. 1:1 대응이 되도록 만드는 것이 거의 불가능하기도 하지만 그런 hash function를 만들어봤자 그건 array 와 다를바 없고 메모리를 너무 차지하게 된다.
- 1. seperate Chaining 기법: Close Hashing 폐쇄해싱
해쉬 테이블 저장공간 외 공간을 활용, Linked List로 중복주솟값을 갖는 데이터들을 연결한다.
중복되는 값이 길어질 수록 연결 노드를 선형적으로 탐색하는 것과 유사해진다.
- 2. Open Addressing Hashing 개방해싱
해쉬 테이블 저장공간 내에서 해당주솟값의 다음 주소값 들 중 빈 공간을 검색하고 저장하는 기법이다.(테이블 확장/ 캐시효율은 높다.) 저장공간 활용도를 높이기 위한 방법이다. 모든 원소가 자신의 해쉬값과 일치하는 주소에 저장된다는 보장이 없다.
데이터 갯수가 적다면 OpenAddressing 이 더 성능이 좋다.
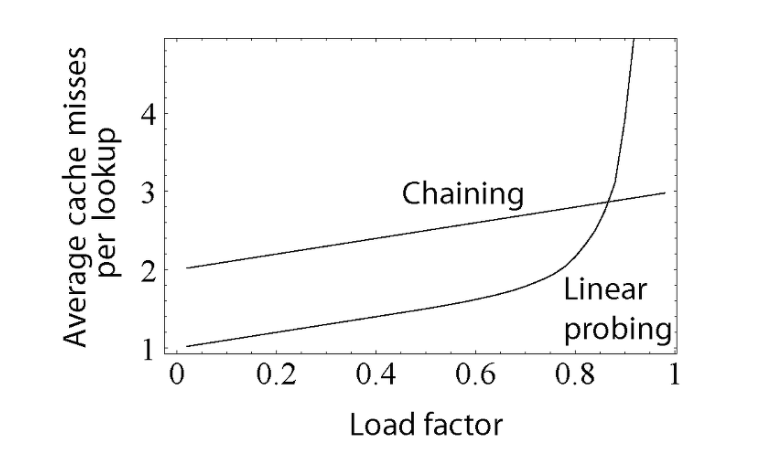
- 선형조사 Linear Probing : 가장 간단한 충돌해결방법, 순서대로 빈 공간을 검색하고 빈 공간에 값을 저장,테이블 경계를 벗어날 경우(마지막 배열공간) 맨 앞으로 돌아온다. 특정 영역에 원소가 몰려있다면 빈 공간을 찾는데 오랜 시간이 걸리게 된다.
- 이차원 조사 : 선형조사보다 보폭을 이차함수로 넓혀 빈 공간을 탐색한다. 특정영역이 몰려있다면 빠르게 벗어날 수 있다. 최악의 경우, 중복되는 인덱스가 여러번 나오면 앞에서 거친 방법들을 한번더 반복한 후에야 빈 공간에 저장할 수 있게 된다.
- 더블해싱 : 두개의 해쉬 함수를 사용
첫번째 해시값으로 해쉬 저장가능여부를 확인하고, 두번째 해시값은 충돌이 일어난 경우 이동할 폭을 얻을 때 사용된다. 이차원조사에서 충돌 후 중복되던 확인 절차 방법을 바꾼 것이다. 두번째 해쉬값까지 중복될 확률은 낮으므로 효과적으로 충돌을 해결하고 빠르게 저장할 수 있게 된다.
> 시간복잡도_O(1)
- 일반적인 경우(충돌이 없는): O(1)
- 최악의 경우 모든 경우에 대해 충돌이 발생한 경우: O(n)
최악의 경우가 있으나 해쉬테이블은 충돌이 발생하지 않는 경우를 기대하고 만들기 때문에 1로 한다.
