[알고리즘] 정렬 | Bubble, Selection, Insertion, Merge, Quick

1. 버블 정렬 (Bubble Sort)

버블 정렬은 인접한 두 원소를 비교하면서 순차적으로 정렬하는 간단한 정렬 알고리즘이다.
이 알고리즘은 배열을 순회하면서 인접한 두 원소의 크기를 비교하여 필요에 따라 교환한다.

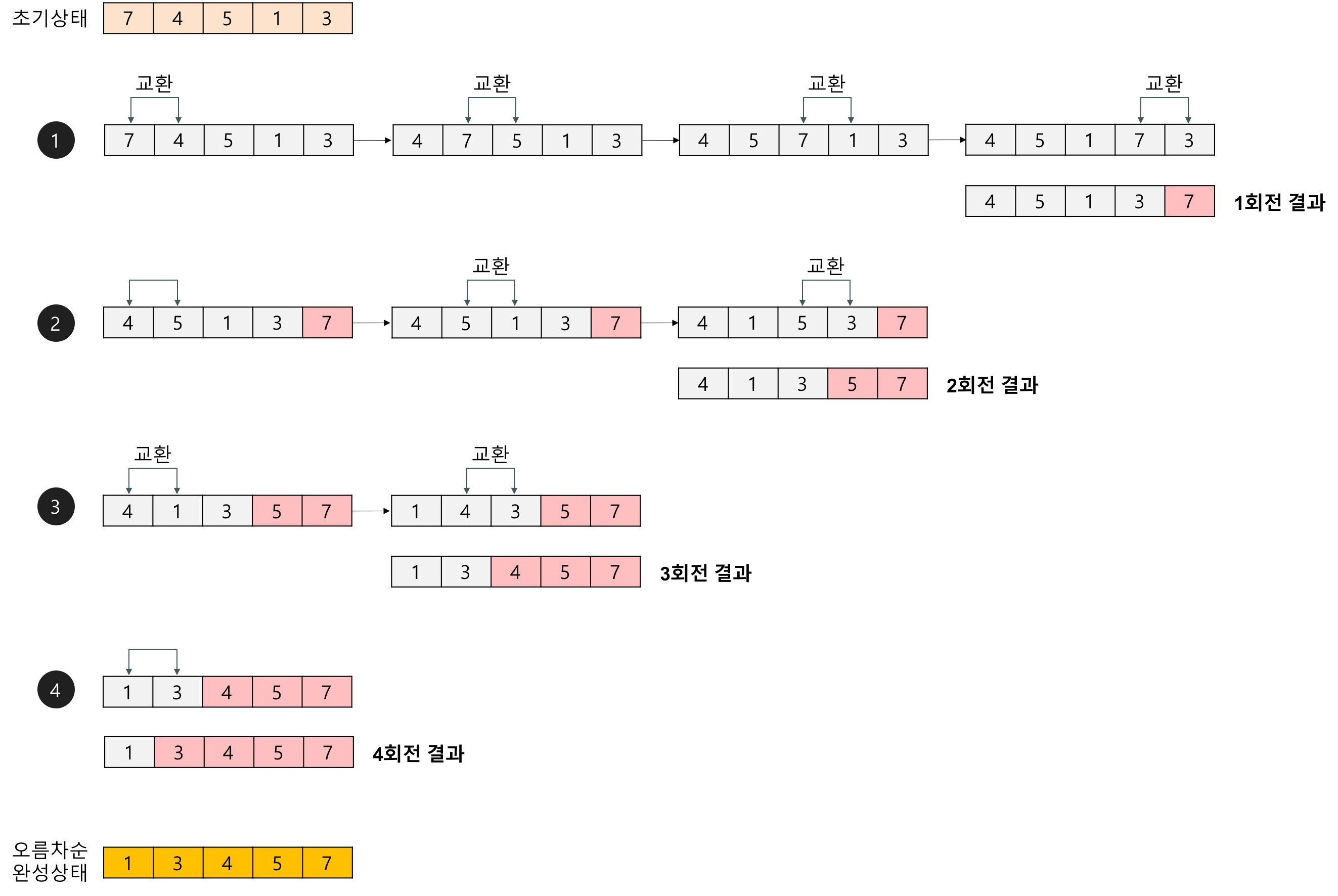
동작

• 왼쪽부터 시작하여 인접한 두 원소를 비교한다.
• 만약 왼쪽의 원소가 오른쪽의 원소보다 크다면 두 원소를 교환한다.
• 끝까지 도달할 때까지 위의 과정을 반복한다.
• 1회전이 완료되면 가장 큰 원소가 맨 뒤로 이동한다.
• 정렬된 원소를 제외하고 이러한 과정을 배열이 정렬될 때까지 반복한다.

시간 복잡도

버블 정렬의 시간 복잡도는 이미 정렬된 배열(O(n))이 아닌 이상 O(N^2) 이다.
n개의 원소를 가지고 버블 정렬을 수행하는 데는 최대의 n×(n−1)/2 번의 비교와 교환이 필요하다.

추가적으로 버블 정렬의 공간 복잡도는 O(1) 이며 버블 정렬은 인접한 두 원소의 크기가 같은 경우에도 교환을 수행하기 때문에 안정적인 정렬 알고리즘이라고 할 수 있다.

자바스크립트로 구현

function bubbleSort(arr) {
    let len = arr.length;

    // 외부 루프: 패스를 반복
    for (let i = 0; i < len - 1; i++) {
        // 내부 루프: 인접한 원소 비교 및 교환
        for (let j = 0; j < len - 1 - i; j++) {
            // 현재 원소와 다음 원소 비교
            if (arr[j] > arr[j + 1]) {
                // 교환
                let temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }

    return arr;
}

2. 선택 정렬 (Selection Sort)

선택 정렬은 배열을 반복하며 최소값(또는 최대값)을 찾아 해당 위치의 원소와 교환하는 방식으로 동작한다. 배열의 첫 번째 위치부터 시작하여 남은 원소들 중에서 가장 작은 값을 찾아 그 값의 현재 위치와 교환한다.

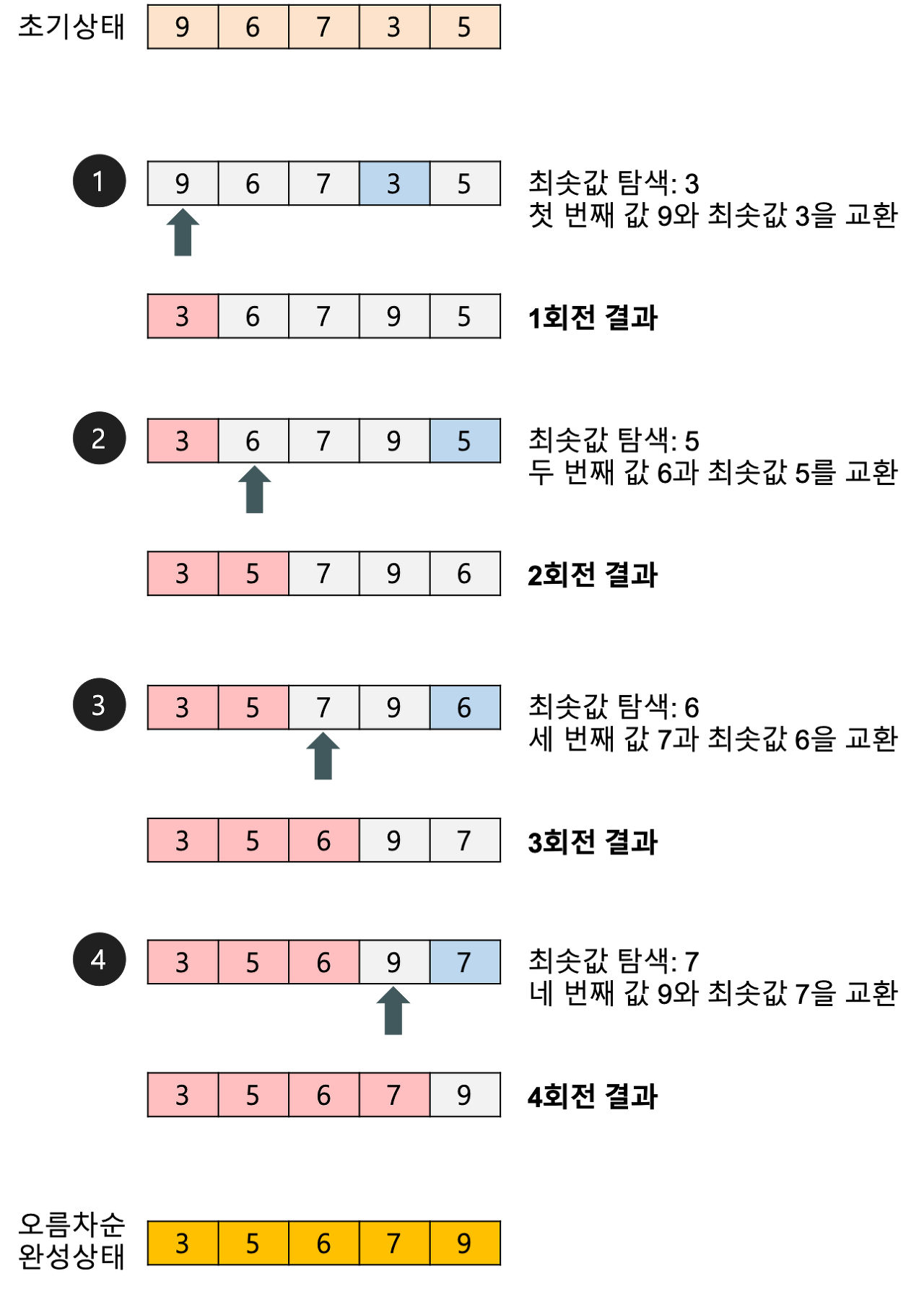
동작

• 가장 작은 값을 찾아 첫 번째 위치의 값과 교환한다.
• 첫 번째 원소를 제외한 남은 배열에서 가장 작은 값을 두 번째 위치의 값과 교환한다.
• 이러한 과정을 배열의 길이만큼 반복한다.

시간 복잡도

선택 정렬의 시간 복잡도는 항상 O(N^2) 이다.
버블 정렬과 마찬가지로 n개의 원소를 가지고 선택 정렬을 수행하는 데는 최대의 n×(n−1)/2 번의 비교가 필요하지만, 교환의 경우 최소값을 찾아 교환하기 때문에 각 패스마다 최대 n−1번이다.
하지만 이는 상수 시간으므로 시간 복잡도에는 영향을 미치지 않는다.

추가적으로 선택 정렬의 공간 복잡도는 O(1) 이며 선택 정렬은 같은 값에 대해 상대적인 위치가 변경될 수 있으므로 안정적인 정렬 알고리즘은 아니다.

자바스크립트 구현

function selectionSort(arr) {
    let len = arr.length;

    for (let i = 0; i < len - 1; i++) {
        let minIndex = i;

        // 현재 인덱스 이후의 원소들을 탐색하며 최소값을 찾음
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }

        // 최소값을 현재 인덱스와 교환
        if (minIndex !== i) {
            var temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }

    return arr;
}

3. 삽입 정렬 (Insertion Sort)

삽입 정렬은 현재 위치에서 그 앞(또는 뒤)의 원소들과 비교하며 자신이 들어갈 위치를 찾아 정렬하는 알고리즘이다. 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 부분과 비교하면서 적절한 위치에 삽입하는 방식으로 동작한다.

동작

• 배열의 두 번째 원소부터 시작하여 정렬을 진행한다.
• 현재 위치의 원소를 정렬된 부분과 비교하여 적절한 위치에 삽입한다.
• 정렬된 부분이 늘어날 때까지 위의 과정을 반복한다.

시간 복잡도

삽입 정렬의 시간 복잡도는 이미 정렬된 배열(O(n))이 아닌 이상 O(N^2) 이다.
삽입 정렬은 비교 횟수가 버블, 선택 정렬보다 적기 때문에 요소들 간의 교환이 더 적게 이루어져 버블, 선택 정렬보다는 성능이 좋을 수 있다.

추가적으로 삽입 정렬의 공간 복잡도는 O(1) 이며 삽입 정렬은 같은 값에 대해 상대적인 위치가 변경되지 않는 안정적인 알고리즘이다.

자바스크립트 구현

function insertionSort(arr) {
    let len = arr.length;

    for (let i = 1; i < len; i++) {
        let current = arr[i];
        let j = i - 1;

        // 정렬된 부분에서 현재 원소의 삽입 위치를 찾아간다.
        while (j >= 0 && arr[j] > current) {
            arr[j + 1] = arr[j];
            j--;
        }

        // 삽입 위치에 현재 원소를 삽입한다.
        arr[j + 1] = current;
    }

    return arr;
}

4. 병합 정렬 (Merge Sort)

병합 정렬은 분할 정복 기법을 사용하여 배열을 정렬하는 알고리즘 중 하나로 배열을 반으로 나눈 후, 각 부분 배열을 재귀적으로 정렬하고, 정렬된 부분 배열들을 병합하여 전체 배열을 정렬한다.

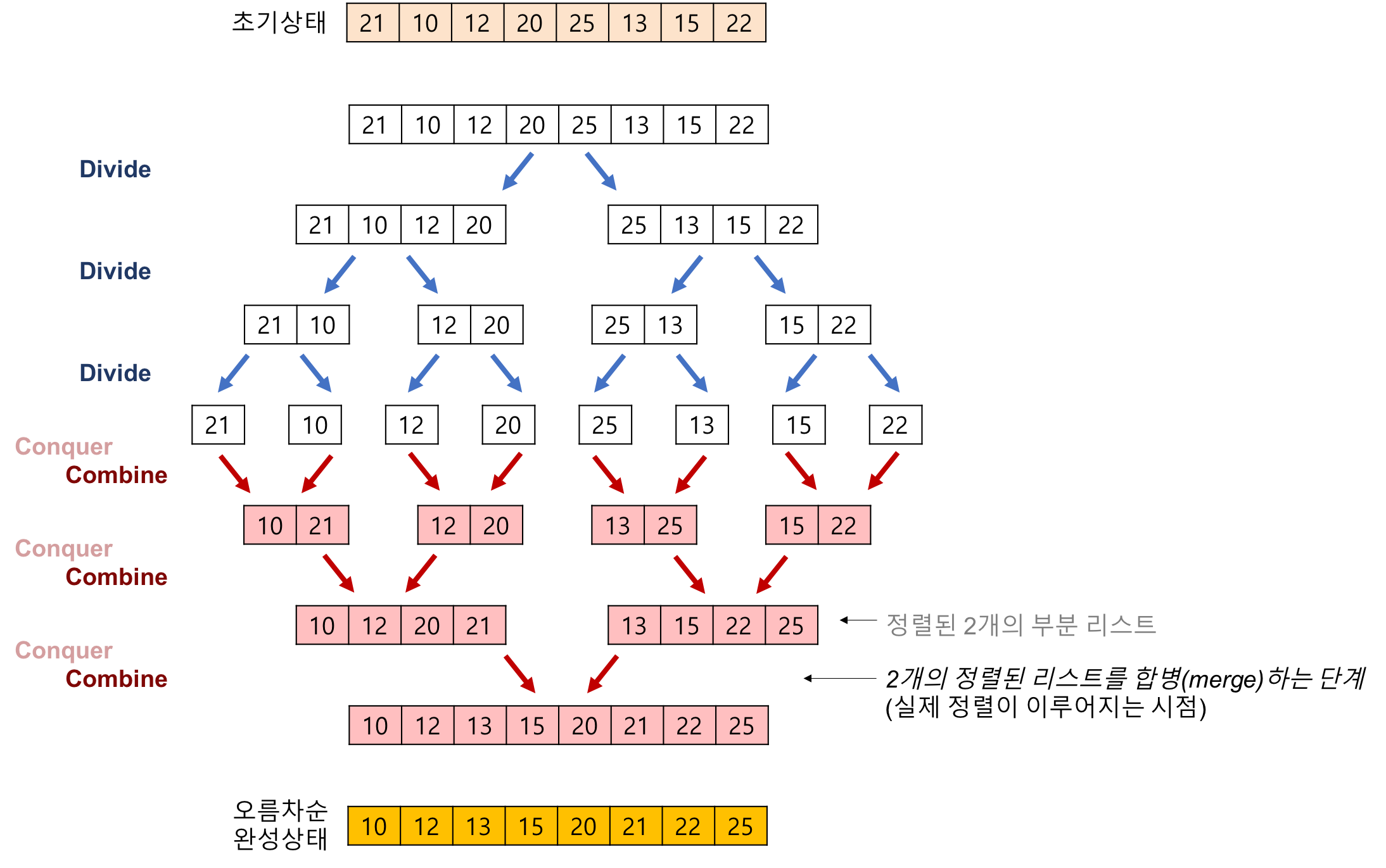
동작

• 주어진 배열을 계속 반으로 나눈다.
• 나눈 각각의 좌우 부분 배열을 비교하면서 작은 값을 먼저 추가한다.
• 재귀적으로 부분 배열을 정렬한다.
• 정렬된 부분 배열들을 병합하여 최종적으로 정렬된 배열을 만든다.

시간 복잡도

병합 정렬의 시간 복잡도는 항상 O(nlogn) 이다. 배열을 반으로 나누는 단계에서 logn이 소요되고, 각 단계에서 배열 전체를 병합하는 단계에서 n이 소요된다.

추가적으로 병합 정렬의 공간 복잡도는 O(n) 이며 병합 정렬은 같은 값에 대해서도 상대적인 순서가 변하지 않는 안정적인 정렬 알고리즘이다.

자바스크립트 구현

function mergeSort(arr) {
    if (arr.length <= 1) {
        return arr; // 기저 조건: 이미 정렬된 배열 또는 길이가 1 이하인 배열
    }

    // 배열을 반으로 나눈다.
    const middle = Math.floor(arr.length / 2);
    const left = arr.slice(0, middle);
    const right = arr.slice(middle);

    // 재귀적으로 부분 배열을 정렬한다.
    const sortedLeft = mergeSort(left);
    const sortedRight = mergeSort(right);

    // 정렬된 부분 배열을 병합하여 최종적으로 정렬된 배열을 반환한다.
    return merge(sortedLeft, sortedRight);
}

function merge(left, right) {
    let result = [];
    let leftIndex = 0;
    let rightIndex = 0;

    // 좌우 배열을 비교하면서 작은 값을 결과에 추가한다.
    while (leftIndex < left.length && rightIndex < right.length) {
        if (left[leftIndex] < right[rightIndex]) {
            result.push(left[leftIndex]);
            leftIndex++;
        } else {
            result.push(right[rightIndex]);
            rightIndex++;
        }
    }

    // 남은 요소들을 결과에 추가한다.
    return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}

5. 퀵 정렬 (Quick Sort)

퀵 정렬은 분할 정복 알고리즘의 일종으로, 평균적으로 매우 빠른 정렬을 제공하는 알고리즘이다. 배열에서 하나의 원소를 선택하고, 이를 기준으로 작은 원소들은 왼쪽으로, 큰 원소들은 오른쪽으로 분할하며 각 부분 배열을 재귀적으로 정렬한다.

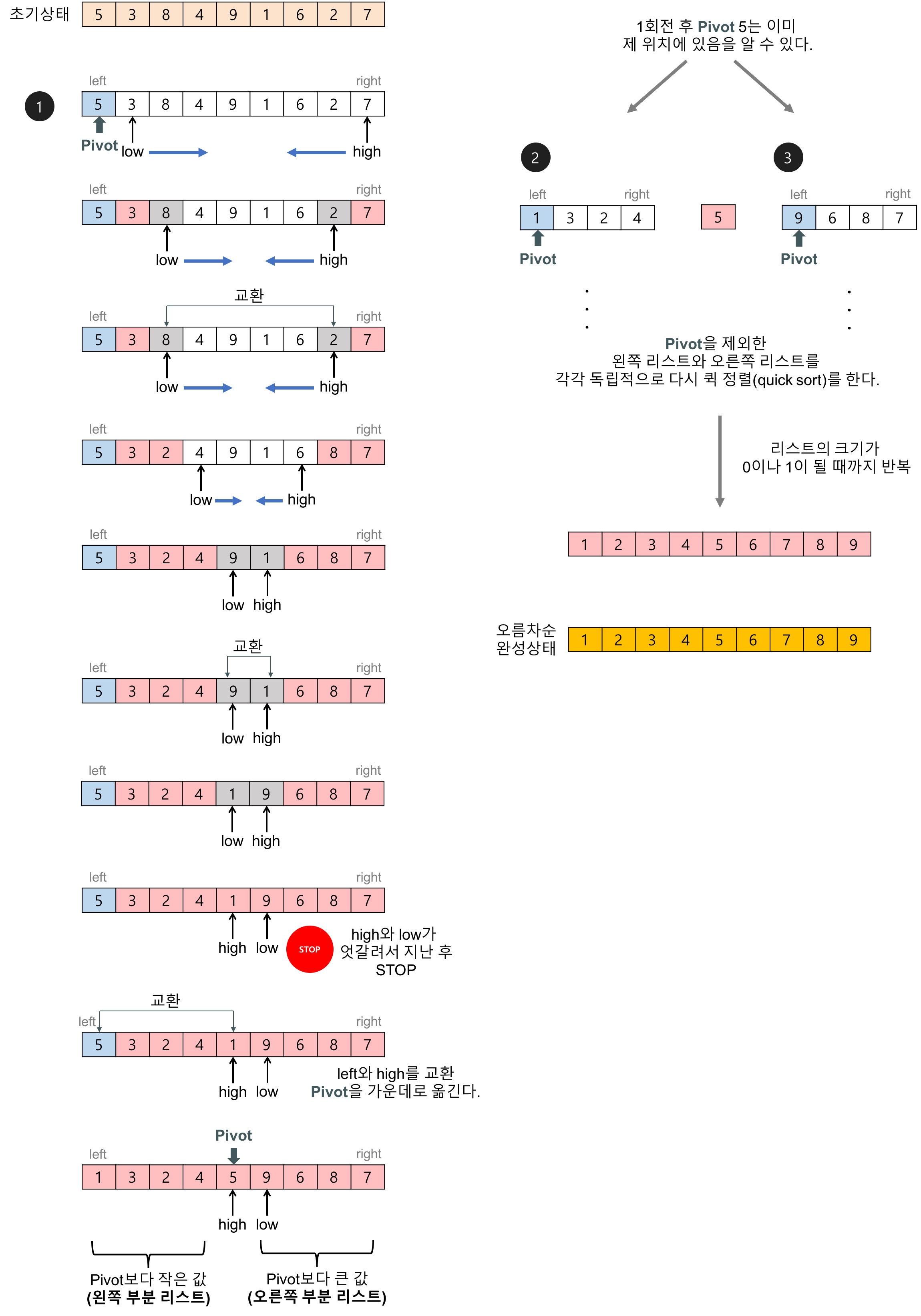
동작

• 배열에서 하나의 원소를 기준점(pivot)으로 정한다.
• pivot을 기준으로 작은 원소들은 왼쪽으로, 큰 원소들은 오른쪽으로 나눈다.
• 나눠진 부분 매열에 대해 재귀적으로 퀵 정렬을 수행한다.
• 각 부분 배열의 정렬이 완료되면 모든 부분 배열들이 결합되어 정렬된 배열이 완성된다.

시간 복잡도

퀵 정렬의 시간 복잡도는 평균 O(nlogn) 이다. 각 분할에 대해 평균적으로 logn번의 비교가 이루어진다.
pivot이 중간에 가까운 값인 경우, 즉 분할이 균등하게 이루어질 경우 성능은 더 좋아진다.
그러나 pivot이 항상 최소 또는 최대값으로 선택되어 분할이 불균형하게 이루어질 경우, 즉 최악의 경우 시간 복잡도는 O(N^2)가 될 수 있다.

추가적으로 퀵 정렬은 동일한 키 값을 가진 원소들의 상대적인 위치가 변할 수 있는 안정적이지 않은 정렬 알고리즘이다.

자바스크립트 구현

function quickSort(arr) {
    if (arr.length <= 1) {
        return arr; // 기저 조건: 이미 정렬된 배열 또는 길이가 1 이하인 배열
    }

    const pivot = arr[0]; // 첫 번째 원소를 피벗으로 선택
    const left = [];
    const right = [];

    // 피벗을 기준으로 작은 원소는 left, 큰 원소는 right에 분할
    for (let i = 1; i < arr.length; i++) {
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }

    // 분할된 부분 배열에 대해 재귀적으로 퀵 정렬을 수행하고, 결합
    return quickSort(left).concat(pivot, quickSort(right));
}