[자료구조] 힙 | Heap, Complete Binary Tree, Priority Queue, Heap Sort

1. 완전 이진 트리(Complete Binary Tree)

완전 이진 트리는 각 노드가 최대 2개의 자식 노드를 갖는 이진 트리의 한 종류로, 모든 레벨에서 왼쪽에서 오른쪽으로 노드가 순차적으로 채워진 구조를 갖는다.

• 모든 레벨에서 노드들은 왼쪽에서 오른쪽으로 순차적으로 채워져야 한다.
• 마지막 레벨은 왼쪽부터 순서대로 채워져야 하지만, 꼭 모든 위치가 채워질 필요는 없다.
• 높이가 h인 완전 이진 트리의 경우, 레벨 0부터 레벨 h-1까지는 모든 레벨이 완전히 체워져 있어야 한다. 즉, 마지막 레벨을 제외한 모든 레벨은 완전히 채워져 있어야 한다.

2. 우선순위 큐(Priority Queue)

우선순위 큐는 각 요소에 우선순위를 할당하고, 그 우선순위에 따라 요소들을 처리하는 자료구조이다. 일반적이 큐와 달리 요소들은 우선순위에 따라 정렬되어 있어 가장 높은 우선순위를 가진 요소가 먼저 처리된다.

• 우선순위 큐는 이진 힙, 이진 탐색 트리 등 다양한 방식으로 구현될 수 있으나, 이진 힙 방식이 많이 사용된다.

3. 힙(Heap)

힙은 특정한 규칙에 따라 정렬된 완전 이진 트리를 기반으로 하는 자료구조이다. 이진 트리의 한 종류로서, 각 노드의 값은 해당 노드의 자식 노드들보다 크거나 작은 특성을 가지며, 이를 통해 최대 힙(Max Heap)과 최소 힙(Min Heap)으로 나뉜다.

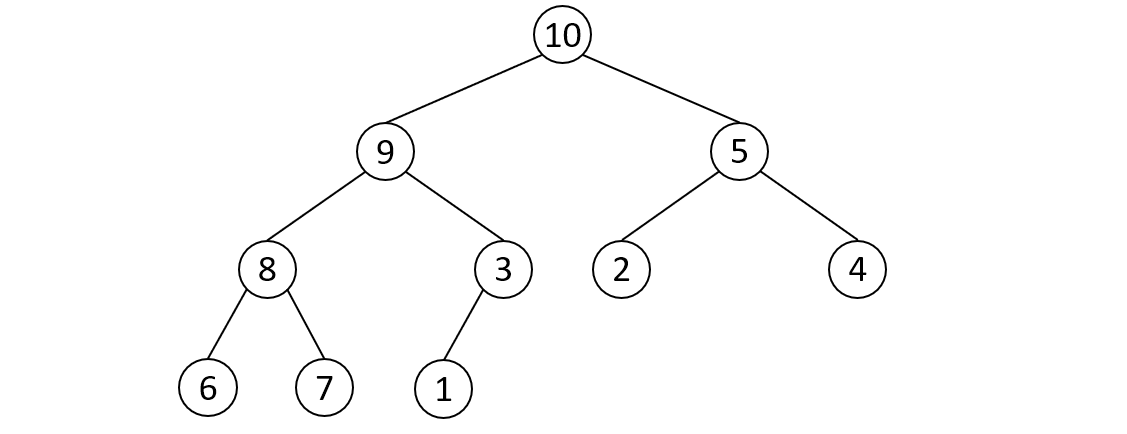
• 최대 힙은 부모 노드의 값이 자식 노드들의 값보다 크거나 같고, 최소 힙은 반대로 각 노드의 값이 자식 노드들의 값보다 작거나 같다.
• 힙은 완전 이진 트리의 형태를 가지며, 마지막 레벨을 제외한 모든 레벨이 왼쪽에서 오른쪽으로 순차적으로 채워져 있다.

배열로 구현하기

힙은 대체적으로 배열로 구현된다. 완전 이진 트리를 기본으로 하기 때문에 비어 있는 공간이 없어 배열로 구현하기에 용이하다.

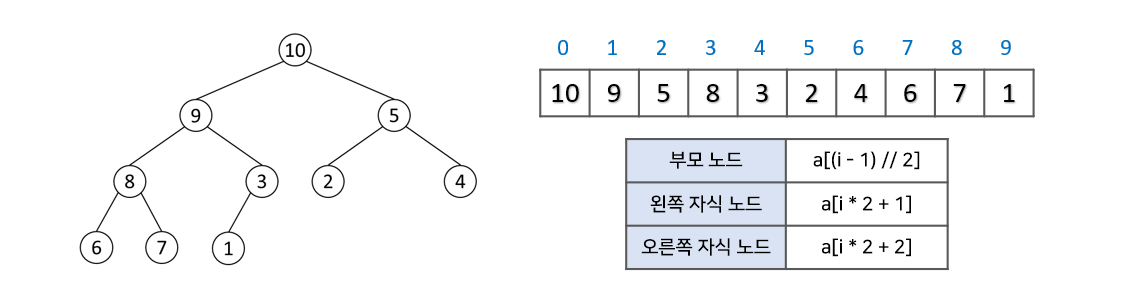
이처럼 루트 노드의 인덱스가 0일 때, 부모 노드의 인덱스는 (i - 1) / 2, 왼쪽 자식 노드는 (i * 2 + 1), 오른쪽 자식 노드는 (i * 2 + 2)로 찾을 수 있다.

삽입 연산

새로운 노드는 힙의 가장 끝에 추가되며, 이후 부모 노드와 비교하여 힙 특성이 만족할 때까지 위치를 재조정하는 과정(heapifyUp)이 이루어진다.

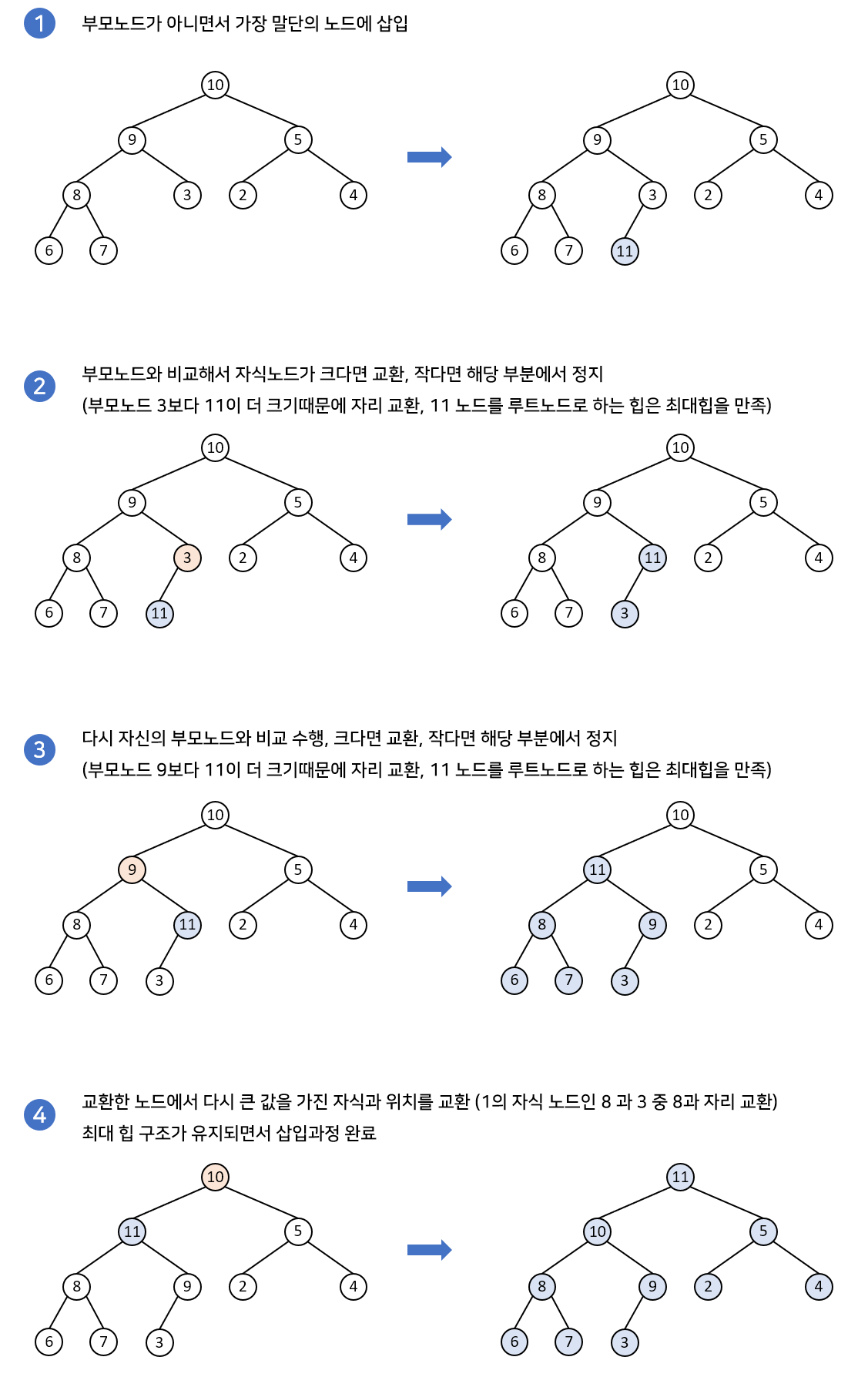
삭제 연산

루트 노드를 삭제하고 반환하며, 마지막 노드를 루트 노드로 옮긴 후, 자식 노드들과 비교하여 힙의 특성을 만족할 때까지 위치를 재조정하는 과정(heapifyDown)이 이루어진다.

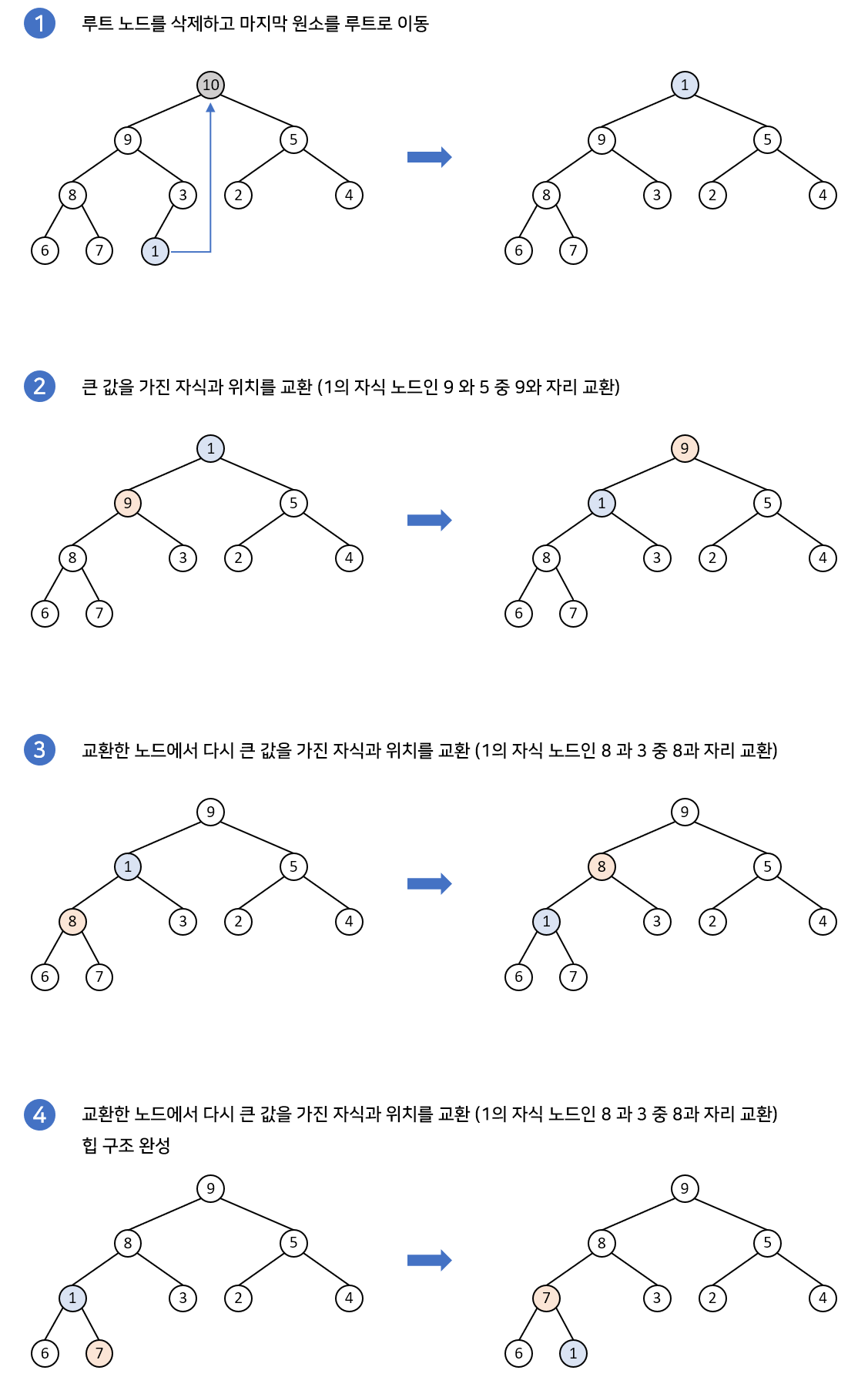
자바스크립트 구현

class MaxHeap {
  constructor() {
    this.heap = [];
  }
  
  // 삽입
  insert(value) {
    this.heap.push(value);
    this.heapifyUp();
  }
  
  swap(index1, index2) {
    [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
  }

  heapifyUp() {
    let currentIndex = this.heap.length - 1;

    while (currentIndex > 0) {
      let parentIndex = Math.floor((currentIndex - 1) / 2);

      if (this.heap[parentIndex] < this.heap[currentIndex]) {
        this.swap(parentIndex, currentIndex);
        currentIndex = parentIndex;
      } else {
        break;
      }
    }
  }

  // 삭제
  delete() {
    if (this.heap.length === 0) {
      return null;
    }

    const max = this.heap[0];
    const last = this.heap.pop();

    if (this.heap.length > 0) {
      this.heap[0] = last;
      this.heapifyDown();
    }

    return max;
  }

  heapifyDown(index = 0) {
    let currentIndex = index;
    let leftChildIndex = currentIndex * 2 + 1;
    let rightChildIndex = currentIndex * 2 + 2;
    let nextIndex = currentIndex;

    if (leftChildIndex < this.heap.length && this.heap[nextIndex] < this.heap[leftChildIndex]) {
      nextIndex = leftChildIndex;
    }

    if (rightChildIndex < this.heap.length && this.heap[nextIndex] < this.heap[rightChildIndex]) {
      nextIndex = rightChildIndex;
    }

    if (nextIndex !== currentIndex) {
      this.swap(currentIndex, nextIndex);
      this.heapifyDown(nextIndex);
    }
  }
}

시간 복잡도

힙에서 최댓값 혹은 최솟값을 검색할 경우 루트 노드의 값만 가지고 오면 되기 때문에 시간 복잡도는 O(1) 이다.
한편, 삽입 및 삭제 연산의 경우 새로운 노드를 추가 및 삭제 한 후에 힙의 특성을 유지하지 위해 재조정하는 과정이 이루어지기 때문에 시간 복잡도는 O(logn) 이다.

힙 정렬(Heap Sort)

힙 정렬은 힙 자료구조를 기반으로 정렬을 수행하는 알고리즘이다. 초기에 주어진 배열을 최대 힙으로 만든 후, 루트 노드(최대값)을 추출하여 배열의 끝에 배치하고, 나머지 요소들을 다시 최대 힙으로 만들어가며 반복한다.

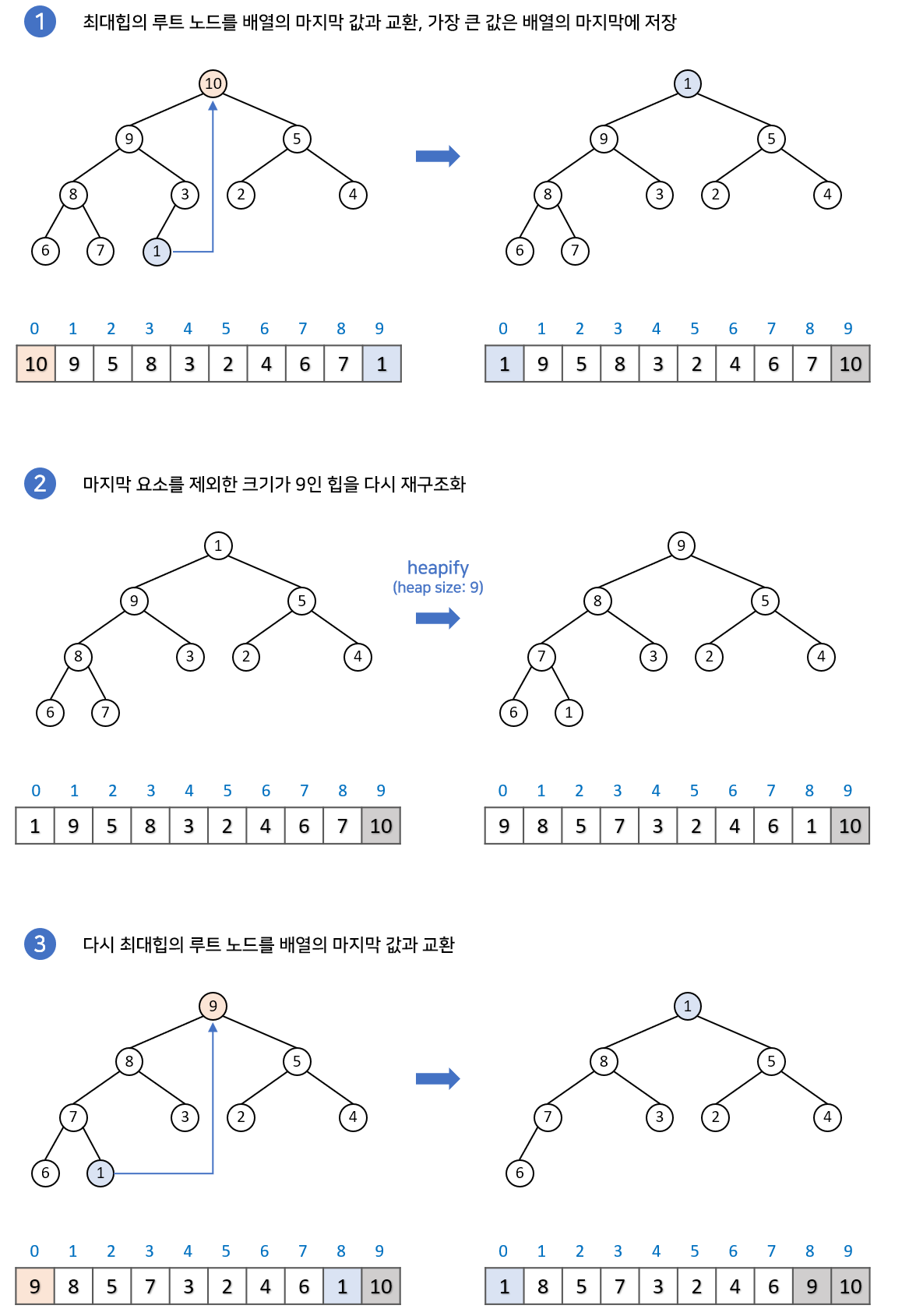
자바스크립트로 구현

function heapSort(arr) {
  // Step 1: 최대 힙(Max Heap) 생성
  buildMaxHeap(arr);

  // Step 2: 힙에서 원소를 하나씩 추출하여 배열을 정렬
  for (let i = arr.length - 1; i > 0; i--) {
    // 루트(최대값)와 배열의 마지막 요소 교환
    [arr[0], arr[i]] = [arr[i], arr[0]];

    // 정렬된 부분을 제외하고 힙을 다시 구성
    heapify(arr, i, 0);
  }

  return arr;
}

// 최대 힙을 만들기 위한 보조 함수
function buildMaxHeap(arr) {
  const n = arr.length;
  // 배열의 중간부터 시작하여 최대 힙 구성
  for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
    heapify(arr, n, i);
  }
}

// 힙을 조정하는 보조 함수
function heapify(arr, n, i) {
  let largest = i;
  const left = 2 * i + 1;
  const right = 2 * i + 2;

  // 왼쪽 자식이 현재 노드보다 크다면 largest 업데이트
  if (left < n && arr[left] > arr[largest]) {
    largest = left;
  }

  // 오른쪽 자식이 현재 노드보다 크다면 largest 업데이트
  if (right < n && arr[right] > arr[largest]) {
    largest = right;
  }

  // largest가 현재 노드와 다르다면 교환하고 재귀적으로 힙 조정
  if (largest !== i) {
    [arr[i], arr[largest]] = [arr[largest], arr[i]];
    heapify(arr, n, largest);
  }
}