이분탐색 이론
(정렬된 수열이어야한다.)
이분탐색은 가장 기초적 이분탐색유형과.
lower_bound
upper_bound
custom_bound
유형이 있다.
이 외에,
매개변수탐색 여부도 있다.
(결정문제(T/F)의 경계값을 찾거나, 단조증가/감소함수의 특장순간을 찾을 수 있다.)
하지만 이 외에 다른 응용이 잘 없다.
(골드1,2가면 있을수도있다.)
즉 이분탐색의 유형은 매우 단조롭다.
기초구현만 할 줄 알고, (에러안나게 하기)
이것이 이분탐색으로 될지 안될지 파악만 할 줄 알면 된다.
[1920] 수찾기

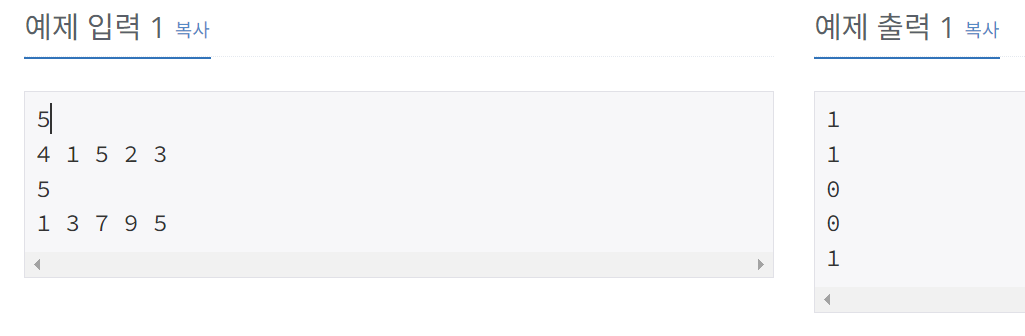
N, M = 10만
이게 저 안에 존재하는지 (T/F)찾는 결정문제
풀이
정렬한뒤 기초적 이분탐색을 구현해서 -1인지 아닌지로 판단하면 됨. O(NlogN)
하지만, 단순히 존재여부만 판단하는 것이므로, 그냥 set자료형의 in 연산자를 활용하면 더 쉽다. O(N)
[10816] 숫자카드2

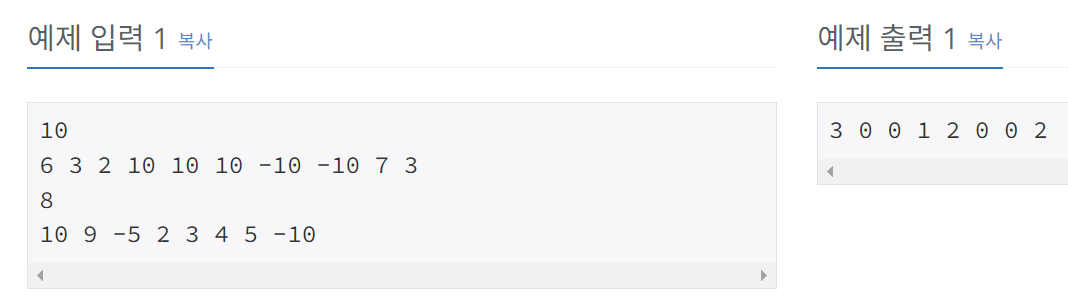
N,M = 50만
배열내 숫자들의범위는 -10억~10억
NlogN 내에 풀기위해 이분탐색.
upper_bound-lower_bound 하면 됨.
(사실 이런문제는 그냥 카운팅해서 푸는 게 더 알맞음. O(N))
연습하는 거라 생각하면 됨.
[2805] 나무자르기
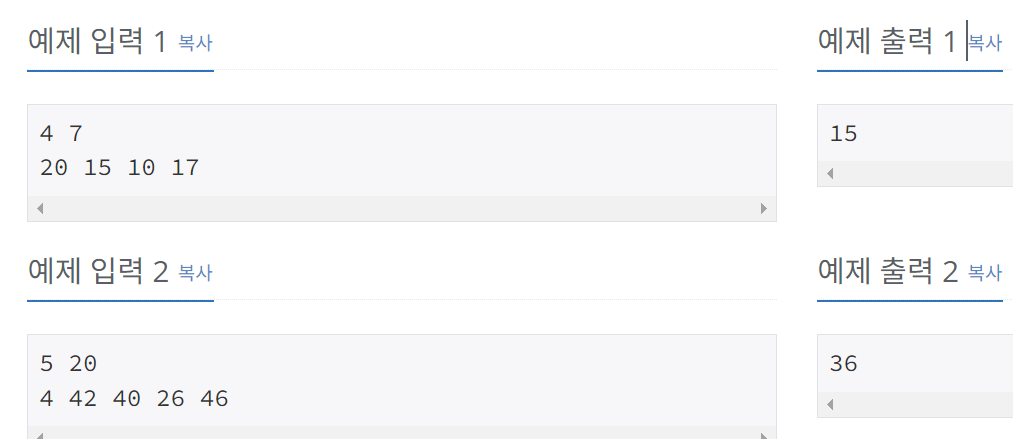
N, M(목표목재)과 배열(나무들 높이)가 주어짐.
15로 지정하면 남는길이 5 0 0 2 의 합 7을 얻을수있음
M을 얻으려면 상한높이를 몇으로설정해야하는가?
풀이
단순히 위치가 어딘가? 이런 문제가아니라,
두 변수를 연결짓는 문제임.
목재 vs 나무 높이. (단조감소)
알고싶은것 : 높이최대값
조건 : 목재
따라서 높이 -> 목재 함수를 구성한 뒤 푸는 매개변수탐색임.
func(목표높이) -> 얻는 목재
를 하나 짧게 구현함.
높이는 최대로 하고싶다 : custom_bound
단조감소관계이다 : 이진 구현시 부등호 방향을 반대로
left, right = 0, max(seq)
max_idx = 0
사실 간단한거라면 함수를 굳이 구성하지말고,
그냥 메인문에서 이진탐색 구현하면서 포함시키는게 더 간소하다.
[1654] 랜선자르기
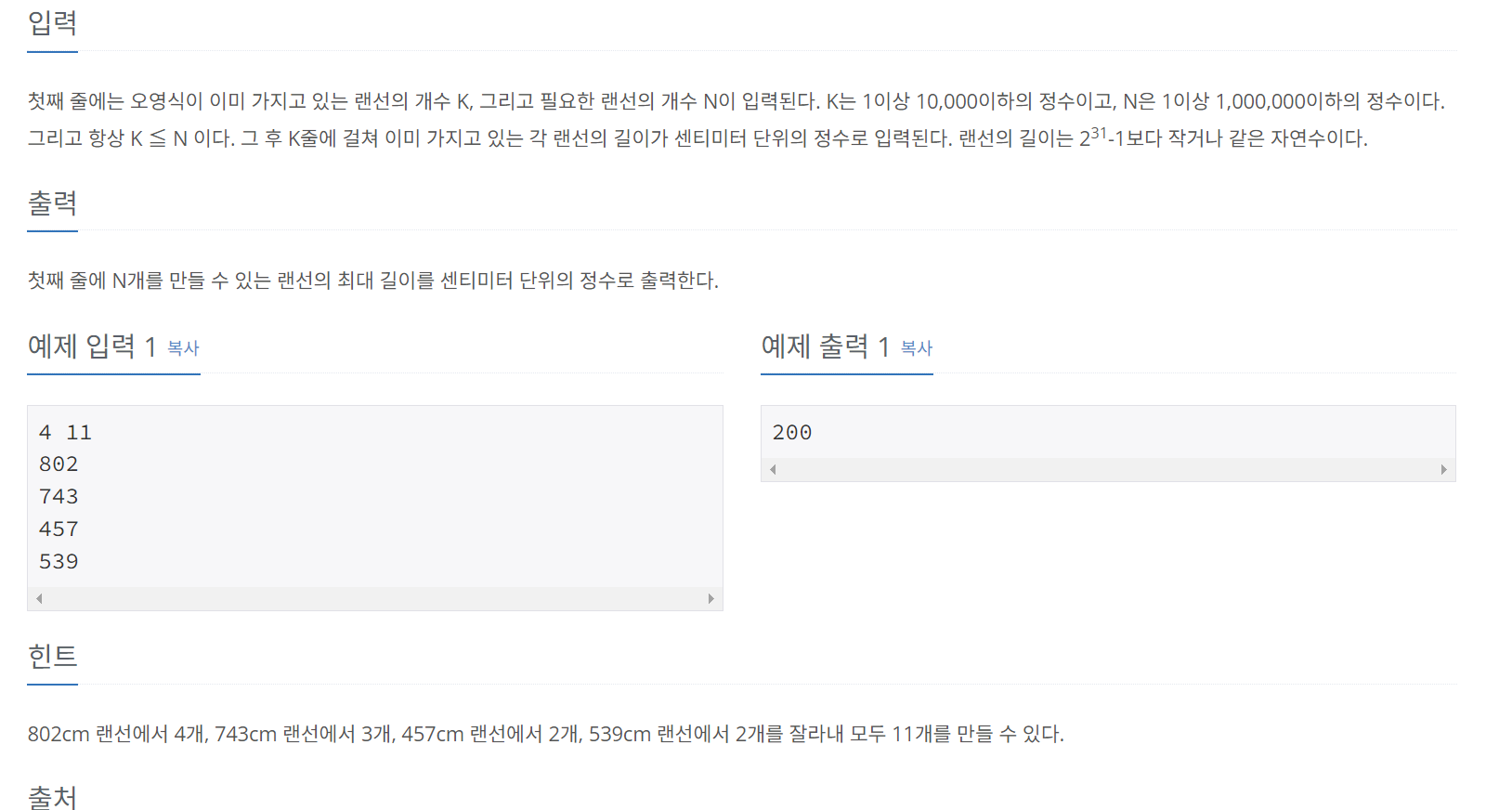
나무자르기랑 같지만, 이젠 잘려나간걸 쓰는게아니라,
자르고 남은게 몇가닥인가 묻는차이
매핑함수 구현만 바뀔뿐 푸는 방법에 차이는 전혀 없음.
자를간격 vs 얻는 갯수 ( 단조감소 함수 )
알고싶은것 : 자를 간격(최대화)
조건 : 얻는 갯수
따라서, 자를간격 -> 얻는 갯수 함수를 만듦
def func(x):
return sum(map(lambda x: x//k, seq))
최대화 하고싶으므로 custom_bound 사용. (custom_bound이므로 max_idx로 구현)
단조감소이므로 부등호방향 바꾸고.
이분탐색 내부 초기값
left, right = 1, min(seq) (0이 함수에 들어가면 zero-division 방지. 자를길이는 최소길이이하)
max_idx = 1
