dp는 크게 타뷸레이션과, 메모이제이션이 있는데
거의 대부분의 실버문제는 타뷸레이션으로 풀리므로
타뷸레이션으로 풀면된다.
2839 설탕배달
문제
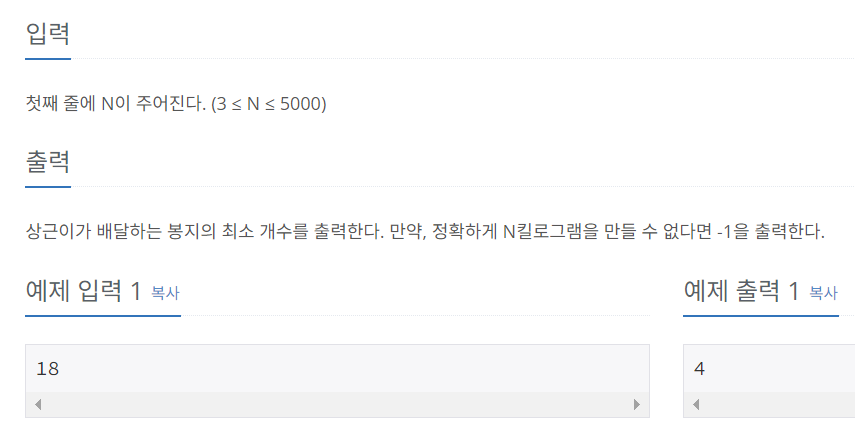
3킬로, 5킬로 이용해서 N킬로를 만들려면 총 몇개가 필요한가.?
풀이:
5는 3의배수가 아니므로 그리디는 쓸수없다.
dp[i] = min(dp[i-3], dp[i-5]) + 1로 해결.
1463 1로만들기
문제:

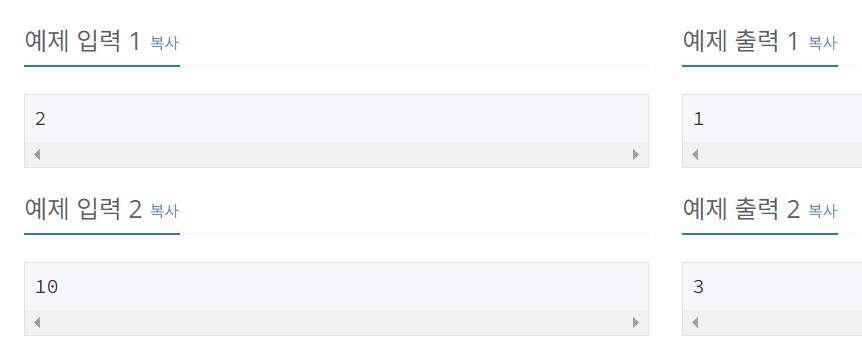
마찬가지로 2로 2번나누는게 3으로한번만나누는거보다 나을수도있어서
그리디로 안풀리는 dp문제이다.
풀이:
dp 구성해서 dp[i] = min(dp[i//3],dp[i//2],dp[i-1])+1
로 푼다.
다만 진짜 저 코드라는건아니고, i%3==0일때만 dp[i//3]을 써야..
너무 세세하게 쓸수없으니 축약표현을 한 셈.
9095 1,2,3 더하기
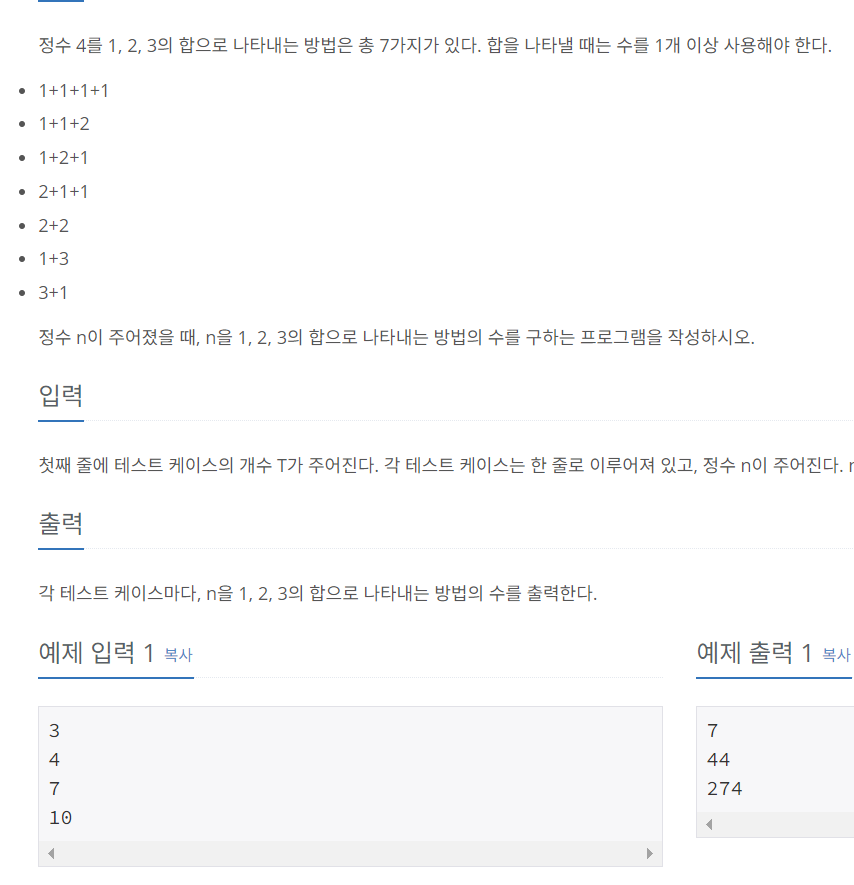
정수 N을 1,2,3의 합으로 나타낼때 방법의 수 구하기
풀이:
dp[i] = dp[i-1]+dp[i-2]+dp[i-3] 이다.
그냥 이렇게 바로떠올려도되고,
지금순간의 상태를생각할 때 경우를나누면,
마지막 선택이 1, 2, 3 중하나이다.
마지막선택이 1이라는건 i-1경우에다 +1한 상태니까 dp[i-1]가지
2라는건 i-2경우에다 +2한 상태인 셈이니 dp[i-2]가지..
11726 2xN 타일링
문제:

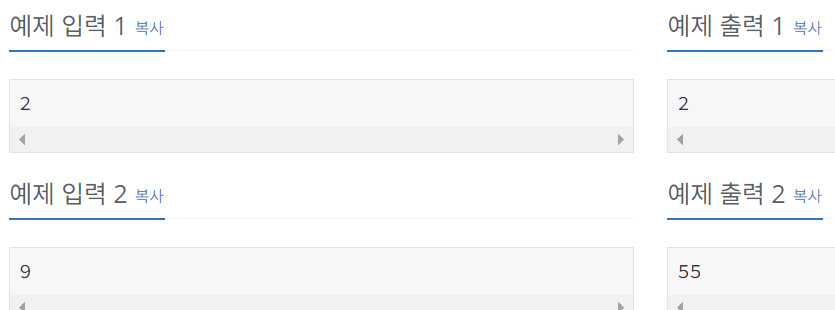
풀이:
i번째 순간 상태를보면.
i번쨰순간에 2x1로 채울경우 == dp[i-1] 가짓수
i번째순간에 1x2로 채움 == dp[i-2] 가짓수
즉 dp[i] = (dp[i-1] + dp[i-2] ) %10007
1149 RGB 거리
문제:
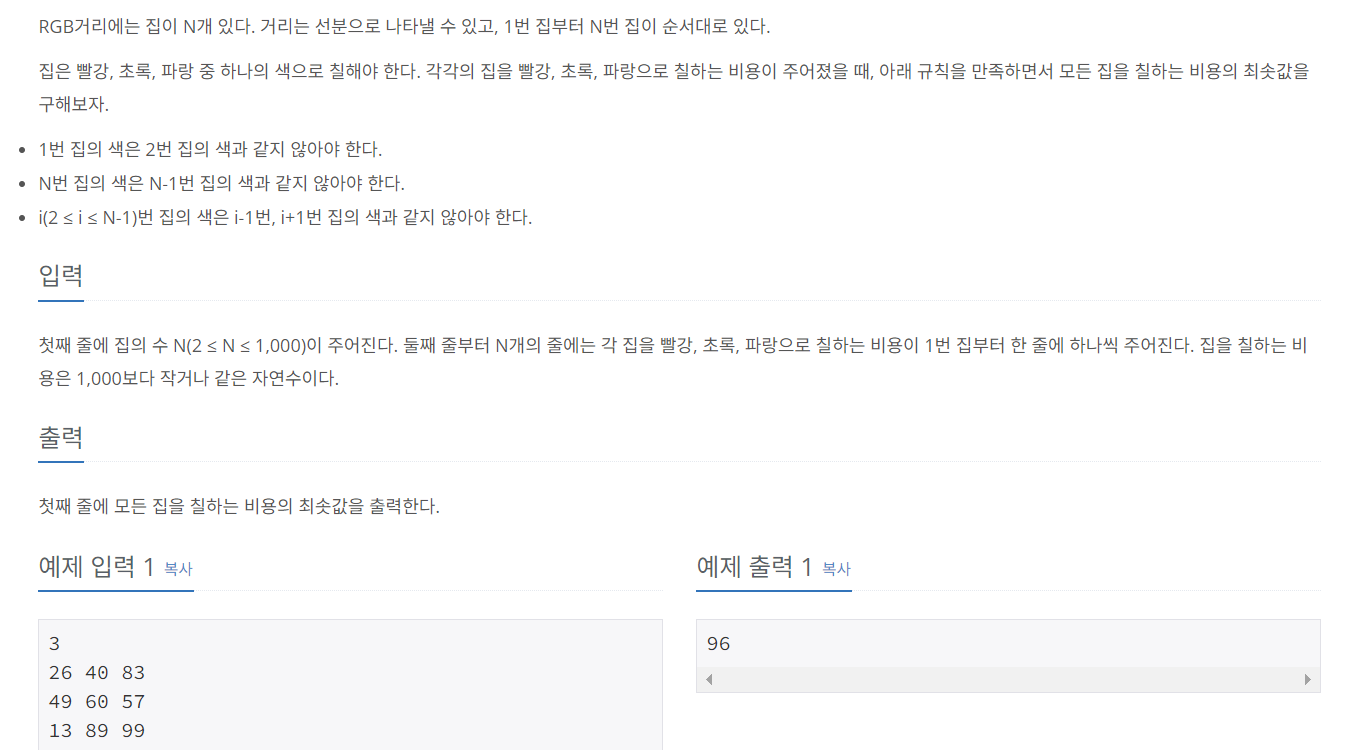
집을 칠하는데 연속한 집의 색은 달라야한다.
이때 R,G,B의 색만으로 모든 집의 색을 칠하는 비용 최솟값.
각 집을 칠하는 비용은 집마다, 색깔(R,G,B)마다 다름
풀이:
마찬가지로 i번째 상태를 관찰하면,
i가 R을 선택하면, i-1은 GB중하나 선택.. 이런식으로하면됨
dp[i][0] = min(dp[i-1][1],dp[i-1][2])+cost[i][0]
이걸 3반복.
아쉽지만 2차원말고 1차원dp로는 풀수가없다.
