완탐유형 골드 정리

완탐유형은 실버라고해서 그렇게 막 엄청쉽고
골드라고해서 어렵고 그렇진 않다.

실버도 어느정도 난이도가 있고,
골드라고 해도 골4까진 실버 1~2와 엇비슷하며, 골3도 아주약간 응용된 느낌이다.

토마토 (7576)

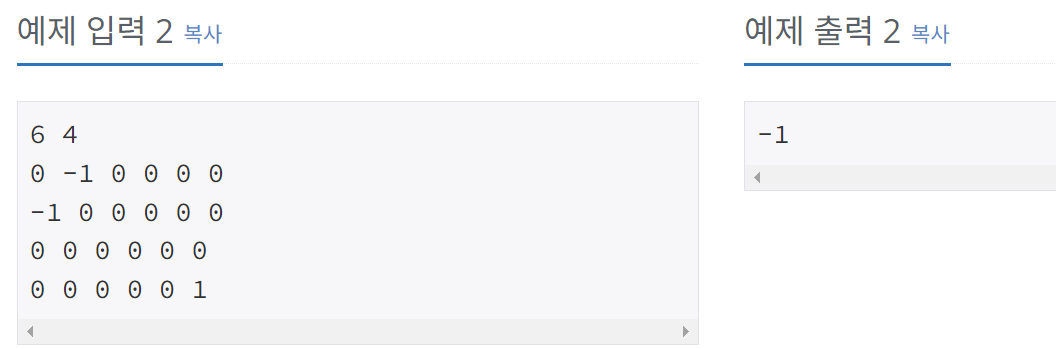
0:익지않은 토마토
1:익은 토마토
-1: 벽 비스무리

익은 토마토가있는데 하루지나면 상하좌우의 안익은토마토도 전염되어서 익는다.
암튼 토마토가 다익는데 얼마나 걸리는지 구하라는 유형.

풀이 : bfs 탐색한 후,
최종적으로 0이존재하는지아닌지를 보고나서.
bfs depth를 얻기위해 (i,j,depth)를 큐에넣고뺴고하면된다.
실버에서도 보이던느낌의 전형적 유형

연구소 (14502)

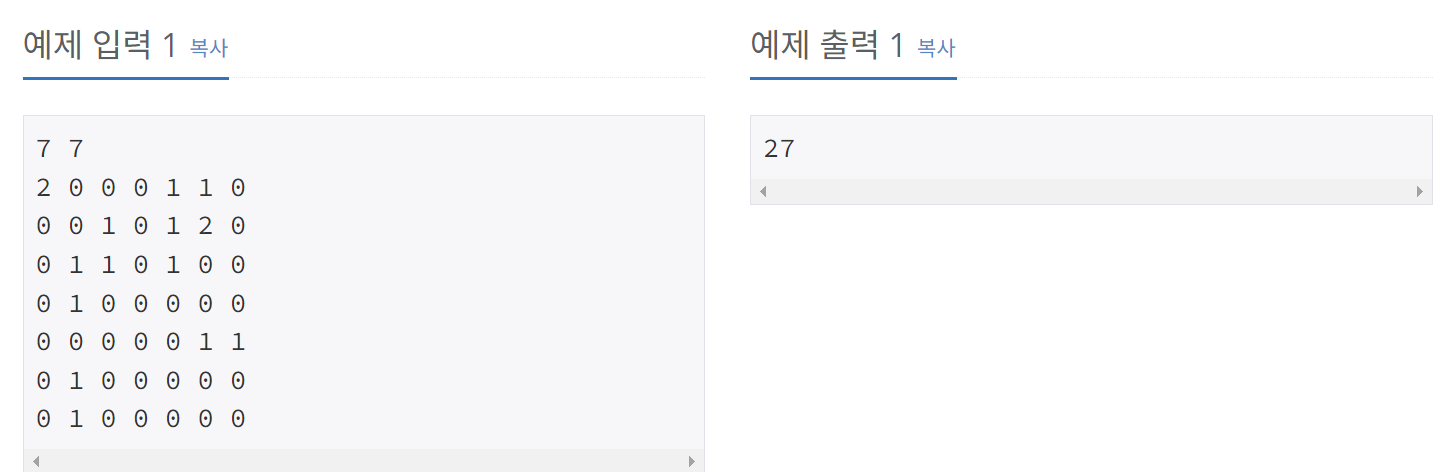
0: 빈칸
1: 벽
2: 바이러스
바이러스가 전염됨.
안전영역(2가 안퍼진 0갯수)의 최대크기 구하기.
0인곳에 벽을 3개 추가로 세울 수 있음.

풀이 : 정말 다행히도 N,M<=8로 엄청나게 작다.
벽을 완전탐색으로 모든곳에 다 미리 세우고
그 이후 bfs로 2를 전파시킨 뒤 안전영역 갯수를 세고
반복.. 하면된다.
반복시 그리드를 되돌리기위해서 deepcopy 사용.

도시분할계획 (1647)

문제 :

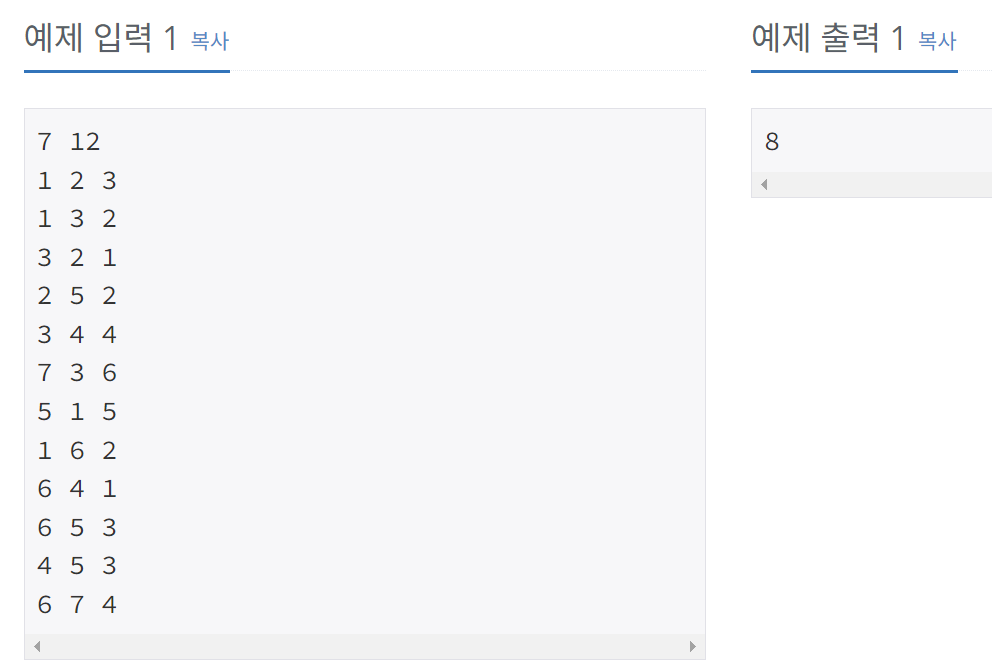
노드수 7, 엣지수 12
1 2 3은 노드 1, 2가 3의 비용으로 연결되어있다는 뜻.

풀이 :

일반적인 그래프탐색이 아니고, 그냥 MST문제.
MST를 구성한 뒤 가장 무거운 엣지 하나만 끊으면 끝.

인구이동(16234)

문제 :

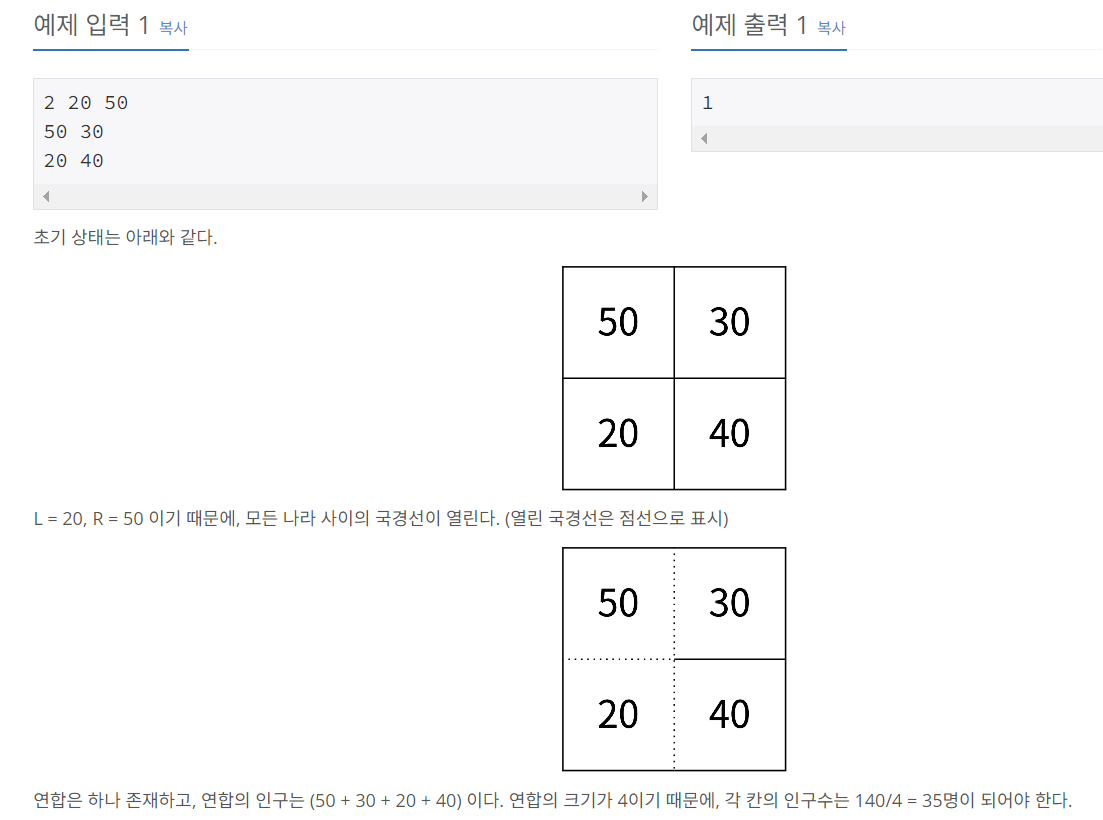
N L R을 주고
인접지역끼리의 차이가 L이상 R이하면 개방됨.
개방된것들끼리는 하루만에 다이동해서 평균으로바뀜.
(소수점버림)

풀이 :
무한루프로 감싸진 2중for로 호출하는 완탐dfs.
inner,outer_count에다, inner_value문제.
(영역내 계산값을 그냥 inner_value로 칭함.)

그 계산결과를 i,j을 이용해서 접근하기위해서는
inner_count_map[i][j] 필요

outer_count : 구역번호
inner_count : 집갯수
inner_sum : 집의 합

inner_mean을 계산해야하고,
그 결과를 배열에 저장하고,
inner_mean을 얻기위해 inner_sum/inner_count 해줌.
mean[inner_count]에 inner_mean을 저장.

i,j->inner_count 매핑해야하는 점은 새로웠음.
다만 그것으로 끝임.

호출부
2중for 그리드순회로, dfs 다돌리고나서

이후 2중for를 다시돌려서 내용을 전부
mean[inner_count]으로 고침.

i,j->inner_count 매핑을 얻기위해
inner_count_map[][]에다 저장하면됨.
즉 사용시 grid[i][j] = mean[inner_count_map[i,j]]
e

이 2중for를 무한루프돌리면됨. outer_count = 0일때까지
그이후 루프인덱스를 답으로 제출