문제 설명
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.
제한 사항
두 수는 1이상 1000000이하의 자연수입니다.
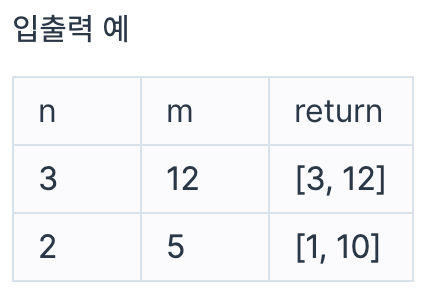
입출력 예 설명
입출력 예 #1
위의 설명과 같습니다.
입출력 예 #2
자연수 2와 5의 최대공약수는 1, 최소공배수는 10이므로 [1, 10]을 리턴해야 합니다.
function solution(n, m) {
let answer = [];
let min;
let max;
let i;
let a = 2;
function aliquot(number){
let arr = [];
i = number;
while(i >= 0){
if( number % i === 0){
arr.push(i);
}
i--;
}
return arr;
}
if(m >= n){
if( m % n === 0){
min = m;
}else{
while(a){
if( (m * a) % n === 0){
min = m * a;
break;
}
a++;
}
}
for( let j = 0; j < aliquot(n).length; j++){
if( m % aliquot(n)[j] === 0){
max = aliquot(n)[j];
break;
}
}
}else{
if( n % m === 0){
min = n;
}else{
while(a){
if( (m * a) % n === 0){
min = m * a;
break;
}
a++;
}
}
for( let j = 0; j < aliquot(m).length; j++){
if( n % aliquot(m)[j] === 0){
max = aliquot(m)[j];
break;
}
}
}
return [max, min];
}하... 한 번에 해결할 줄 알았는데 지저분함이 확연히 보인다.
function solution(n, m) {
const gcd = (m, n) => {
let r = (m % n);
return (r) ? gcd(n, r) : n;
}
return [gcd(m, n), ((m * n) / gcd(m, n))];
}def solution(n, m):
mini = min(n, m)
print(mini)
li = []
for i in range(1, mini + 1):
if (n % i == 0) and (m % i == 0):
li.append(i)
gcd = max(li)
answer = [gcd, int((m * n) / gcd)]
return answer- 최소 공배수 = (두 수의 곱) / 최대 공약수

