Linear system 은 연립방정식이다.

위와 같은 표에서 각 변수(varibale) 인 Weight, Height, Is_smoking 이 Life-span에 얼마만큼 영향을 주는가를 알고싶다고 하자.
그러면 다음과 같은 방정식을 세울 수 있다. 이런 연립방정식들의 집합
을 Linear system 이라고 부른다.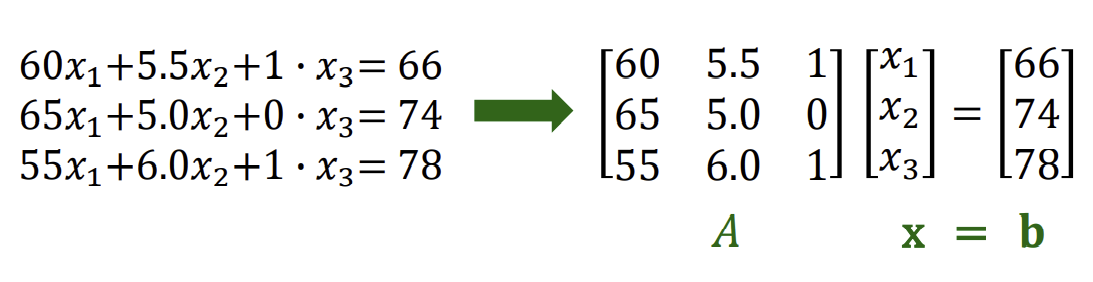
즉, 이렇게 연립 방정식을 "하나의" 행렬을 이용한 방정식으로 바꿀수 있다.
이때 행렬$A$의 원소들을 계수(coefficients)라 한다.

위와같은 방정식 $Ax = b$는 $A$가 ($n$x$n$)정방 행렬일 때 역행렬인 $A^{-1}$을 이용하여 풀 수 있다.

$x = A^{-1}b$

이때 행렬 $A$의 역행렬 $A^{-1}$가 존재한다면(invertible) 유일한 해를 가지게 된다. 하지만 행렬 $A^{-1}$가 존재하지 않는다면(not_invertible) 해가 없거나 무수히 많은 해를 가지게 된다.

현실세계의 문제로 접근할때 는 행렬 A가 정방 행렬이 아니라 행의 개수가 열의 개수 보다 많은 직사각 행렬(Rectangular Matrix)일 경우가 많을 것이다. 즉 변수의 수보다 주어진 데이터의 수가 많은 경우이다.

이렇게 변수의 수(열의 갯수)보다 데이터의 수(행의 개수)가 많을때는 Linear system이 해를 가지지 않게 된다.
위와 같이 해가 존재하지 않을때 최적해를 찾아갈수 있는 방법들을 머신러닝이라고 할 수 있다.