SVD(Singular Value Decomposition) - 특이값 분해

특이값 분해는 차원축소 기법인(PCA)에서 사용된다.

SVD 의 정의

$m$ x $n$ 행렬 $A$가 있을 때 이 행렬 A는 다음과 같이 분해될수 있다.

$A = \ U\sum{}V^T = \ (rotate)(stretch)(rotate)$

---

$U$ = ($m$ x $m$) orthogonal matrix
$\sum$ = ($m$ x $n$) diagonal matrix
$V$ = ($n$ x $n$) othogonal matrix
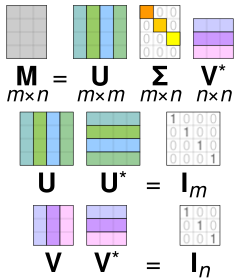그림에서 *는 transpose를 의미한다.
https://ko.wikipedia.org

1.orthogonal matrix가 가지는 성질:
$UU^T=U^TU=I$, $\quad U^{-1}=U^T$
$VV^T=V^TV=I$, $\quad V^{-1}=V^T$

$U$, $\sum$, $V$가 의미하는바는 무엇일까?

먼저 $A = \ U\sum{}V^T$의 양변에 $A^T$를 곱해준다면 $A^TA$는 symmtric, positive semidefined matrix가 될것이다.

($m$ x $n$) 행렬 A가 있을 때 항상 Symmetric, positive semidefined matrix인$S=A^TA$ 를 만들 수 있다.

$A^TA = \ (V\sum{}^TU^T)U\sum{}V^T$

이때 가운데의 $U^TU$는 $U$=othogonal matrix이기 대문에 $U^TU=I$가 된다.

$A^TA = \ V\sum{}^T\sum{}V^T$

$A^TA$는 symmetric, positive semidefined matrix라고 했다.

• symmetric의 성질 - 고유벡터(eigen vector)들은 직각(orthogoanl)하다.
• positive semidefined matrix의 성질 - 고유값(eigen value)들은 양수이다.

따라서 행렬 $A^TA$ 는 항상 다음과 같이 대각화 할 수 있다.
따라서 $A^TA$ 에 대한 고유값 분해(Eigen decomposition)를 하면

$V$ = $A^TA$의 고유벡터들의 행렬
$\sum{}^T\sum{}$ = 대각성분이 고유치고 나머지는 0인 행렬
$V^T$ = $V$는 orthogonal matrix이므로 $V^{-1}=V^T$

만약 위처럼 $A = \ U\sum{}V^T$의 왼쪽이 아닌 오른쪽에 $A^T$를 곱했다면 다음과 같은 결과가 나온다.(과정은 위와 동일하다)

$AA^T = \ U\sum{}^T\sum{}U^T$