1.1 배경
1.1.1 불 대수
불 대수는 참(true)/거짓(false), 예/아니오, 켜짐/꺼짐 같은 불(2진수)값을 다루는 대수학이다.
컴퓨터는 진수를 표현하고 처리하는 하드웨어이기 때문에 2진수를 입력을 가공해 2진수 출력을 하는 불 함수를 정의하고 분석하는 것이 컴퓨터 아키텍처를 구축하는 첫 단계가 된다.
-
진리표 표현
불 함수를 정의하는 가장 쉬운 방법으로, 함수의 입력값들과 결과값을 나란히 표로 나타낸 것이다.
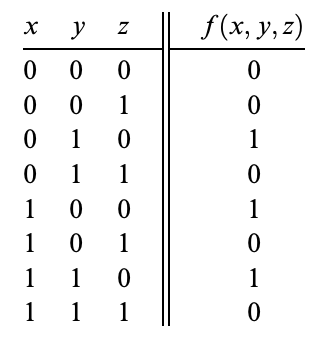위 그림의 앞쪽 x, y, z 부분은 함수 입력값이 될 수 있는 모든 2진 값 조합이다. 마지막 열은 해당 입력에 대한 함수 값이다. -
불 표현식
불 함수를 진리표가 아니라 수식처럼 표현도 가능하다.
예를 들어 기본적인 불 연산인 And, Or Not은 각각 X · Y, X + Y, X'으로 표현된다. -
정준 표현
어떤 함수의 진리표를 바로 불 표현식으로 만들 수 있다.
함수값이 1인 항의 입력값을 And연산으로 묶고 이렇게 묶인 항들을 Or연산으로 합치면 주어진 진리표와 동등한 불 표현식을 얻을 수 있다.
위의 진리표를 예시로 정준 표현을 얻어보면, x'yz'+xy'z'+xyz'이라는 진리표와 동일한 의미의 불 표현식을 얻을 수 있다.
1.1.2 게이트 논리
게이트는 불 함수를 구현한 물리적 장치다. 우리는 하드웨어 설계자로서 기본 게이트들로 서로 연결된 조합 게이트를 통해 더 복잡한 기능을 구현할 것이다.
논리 게이트들은 내부와 외부, 두 가지 관점으로 바라볼 수 있다. 아래 그림의 오른쪽은 게이트의 내부 아키텍처, 즉 구현(implementation)을, 왼쪽은 게이트의 인터페이스(interface), 즉 칩의 외부에 노출된 입력 핀과 출력 핀들을 그린 것이다.
1.1.3 실제 하드웨어 구성
위의 그림에서 보았듯이, 입력 값 3개의 And연산을 해주는 게이트를 사용할 때마다 And게이트 2개로 매번 만들기에는 비효율적이다.
이런 문제를 해결하기 위해서 기본 게이트들처럼 조합 게이트도 하나의 칩으로 만들어서 그 칩을 앞으로 기본 구성 블록으로 사용하면 된다.
1.1.4 하드웨어 기술 언어
오늘날 하드웨어 설계자들은 맨손으로 뭔가를 만들지 않는다. 대신 컴퓨터에서 하드웨어 기술 언어(Hardware Description Language)라는 도구를 사용해서 칩 아키텍처를 설계하고 최적화 한다.
- 예제: Xor 게이트 제작
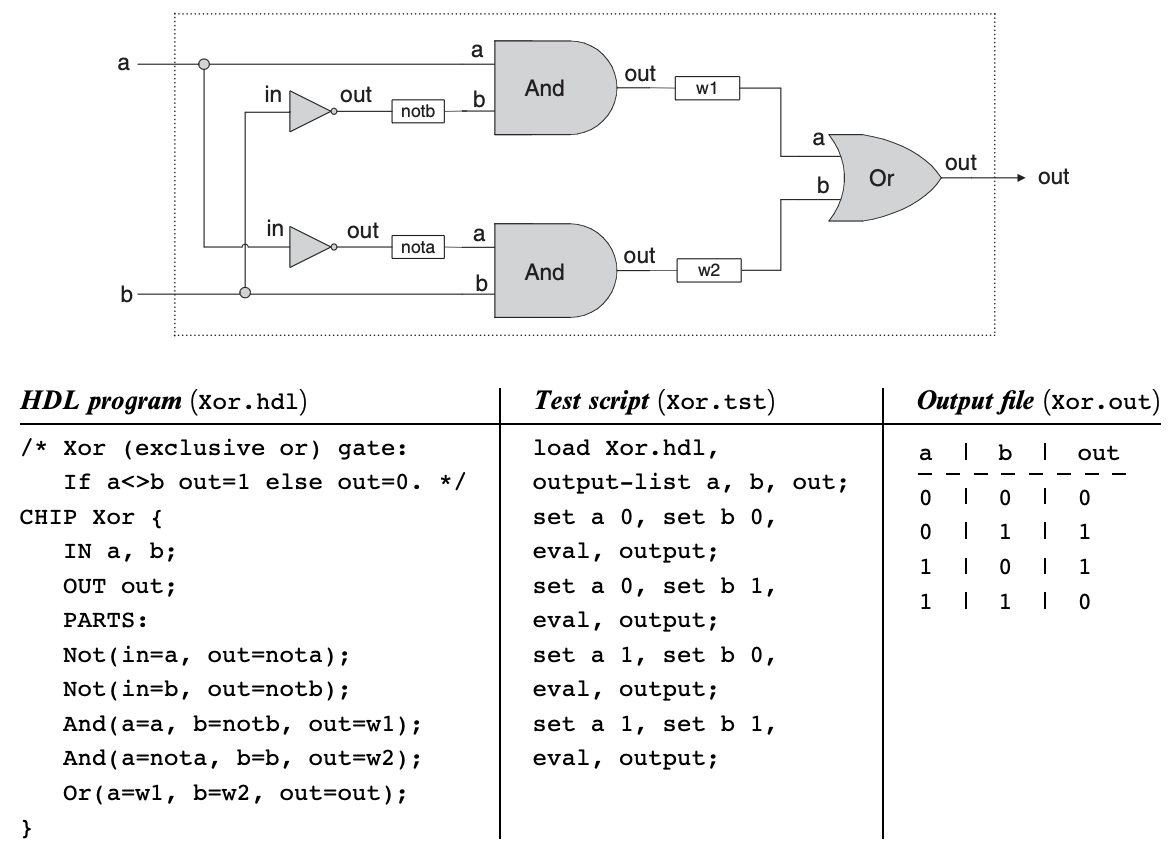
HDL의 헤더 부분에서는 칩 인터페이스를 정의한다. 칩의 이름과 입력 및 출력 이름을 명시한다. 파트는 해당 칩의 내부 구현을 담당한다. 헤더에서 명시된 입력을 각종 불 함수를 사용해 원하는 출력값을 만들어 낸다.
테스트 스크립트는 설계한 칩을 실행시킨다. 실행하고자 하는 칩을 불러와서 입력 값을 설정하고 실행한다. 실행이 끝나고 나면 입력 값의 출력 데이터를 기록한 .out 파일을 생성한다.
1.2 명세
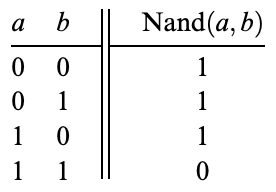
1.2.1 Nand 게이트
Nand 게이트는 다른 모든 게이트들의 기초가 되는 게이트다. Nand는 다음과 같은 불 함수를 계산한다.
1.2.2 기본 논리 게이트
-
Not
단일 입력 Not 게이트는 '컨버터(converter)'라고도 불리며, 입력값을 반전시킨다.
-
And
입력값이 둘다 1일 경우에 1을, 그 외에는 0을 반환한다.
-
Or
입력값 중 적어도 하나가 1일 때 1을, 그 외에는 0을 반환한다.
-
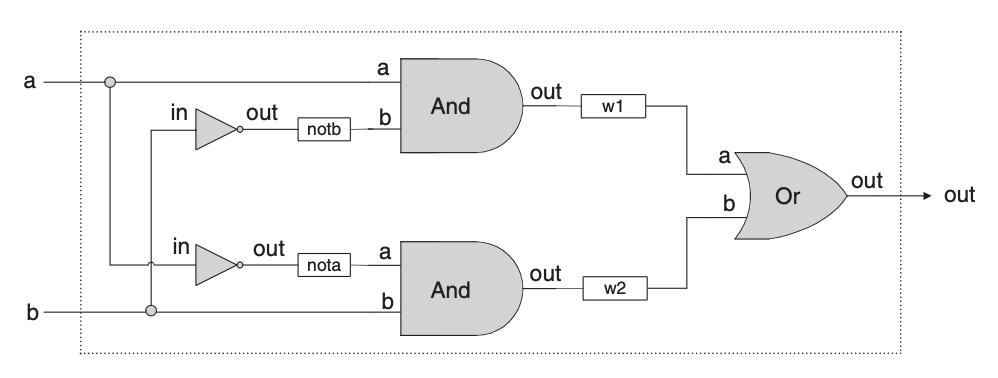
Xor
'배타적 논리합'이라고도 불리는 Xor 함수는 두 입력값이 다를 경우 1, 그 외에는 0을 반환한다.
-
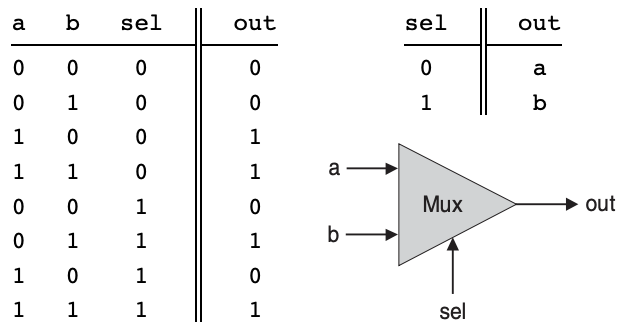
멀티플렉서
'선택 비트'입력에 따라서 두 개의 '데이터 비트'입력 중 하나를 선택해 반환한다.
-
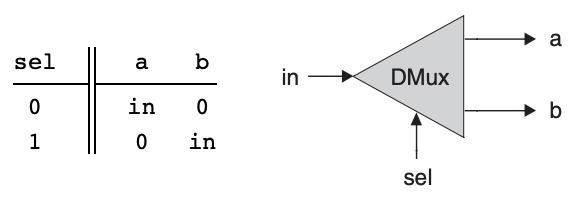
디멀티플렉서
멀티플렉서와 정반대 기능을 한다. '선택 비트'에 따라 두 출력선 중 하나를 선택해 입력 신호를 반환한다.
1.3 구현
몇가지 중요하다고 생각하는 칩만 적어놓았으니 나머지 칩들은 Chapter 1 프로젝트 구현 코드를 참고하라
1.3.1 And
CHIP And {
IN a, b;
OUT out;
PARTS:
// Put your code here:
Nand(a=a, b=b, out=nandAB);
Nand(a=nandAB, b=nandAB, out=out);
}1.3.2 Xor
CHIP Xor {
IN a, b;
OUT out;
PARTS:
// Put your code here:
Not(in=a, out=notA);
Not(in=b, out=notB);
And(a=a, b=notB, out=AandNotB);
And(a=notA, b=b, out=BandNotA);
Or(a=AandNotB, b=BandNotA, out=out);
}1.3.3 Mux16
16비트 게이트를 설계할 때에는 1비트 게이트를 이어붙혀 설계했다.
CHIP Mux16 {
IN a[16], b[16], sel;
OUT out[16];
PARTS:
Mux(a=a[0], b=b[0], sel=sel, out=out[0]);
Mux(a=a[1], b=b[1], sel=sel, out=out[1]);
Mux(a=a[2], b=b[2], sel=sel, out=out[2]);
Mux(a=a[3], b=b[3], sel=sel, out=out[3]);
Mux(a=a[4], b=b[4], sel=sel, out=out[4]);
Mux(a=a[5], b=b[5], sel=sel, out=out[5]);
Mux(a=a[6], b=b[6], sel=sel, out=out[6]);
Mux(a=a[7], b=b[7], sel=sel, out=out[7]);
Mux(a=a[8], b=b[8], sel=sel, out=out[8]);
Mux(a=a[9], b=b[9], sel=sel, out=out[9]);
Mux(a=a[10], b=b[10], sel=sel, out=out[10]);
Mux(a=a[11], b=b[11], sel=sel, out=out[11]);
Mux(a=a[12], b=b[12], sel=sel, out=out[12]);
Mux(a=a[13], b=b[13], sel=sel, out=out[13]);
Mux(a=a[14], b=b[14], sel=sel, out=out[14]);
Mux(a=a[15], b=b[15], sel=sel, out=out[15]);
}1.3.4 Mux4Way16
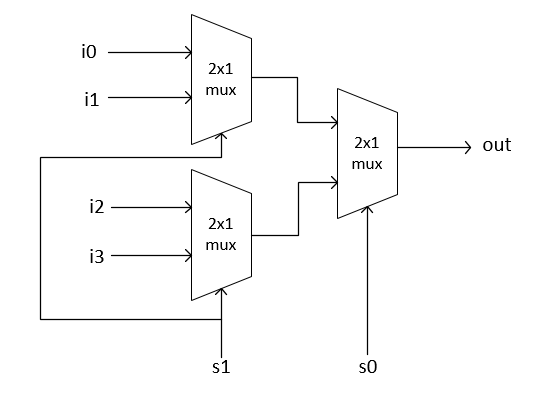
토너먼트 형식으로 일전에 설계한 2X1 Mux로 4개의 입력을 2개로 추리고 추려진 2개의 입력중 마지막 Mux로 최종 출력값을 결정한다. 이때, 선택 비트를 2bit로 늘려서 첫 연산과 마지막 Mux 연산에 각각 선택 비트 한개씩을 사용한다.
CHIP Mux4Way16 {
IN a[16], b[16], c[16], d[16], sel[2];
OUT out[16];
PARTS:
// Put your code here:
Mux16(a=a, b=b, sel=sel[0], out=muxAB);
Mux16(a=c, b=d, sel=sel[0], out=muxCD);
Mux16(a=muxAB, b=muxCD, sel=sel[1], out=out);
}