이 장에서는 논리 게이트를 사용해 숫자를 어떻게 표현하고 계산할지 고민하고, 1장에서 만든 논리 게이트를 사용해 온전히 작동하는 산술 논리 연산 장치를 완성할 것이다.
2.1 배경
- 2진수
컴퓨터는 수를 2진수로 다룬다.
19라는 수를 나타내고자 하면 10011(2진수) = 2^4×1 + 2^3×0 + 2^2×0 + 2^1×1 + 2^0×1 으로 나타날 것이다. - 2진 덧셈
2개의 2진수를 더하려면 기존 덧셈과 마찬가지로 가장 오른쪽(최하위 비트)부터 가장 왼쪽(최상위 비트)까지 같은 자리의 수끼리 자리올림수까지 고려해 더해주면 된다.
만약 마지막 비트를 더하고 나서 자리올람수가 1이라면, 오버플로가 발생한다. - 부호가 있는 2진수
부호를 나타내기 위해 대부분의 컴퓨터는 2의 보수(2's complement) 방식을 이용한다.
X의 보수 = 2^n-X (x가 0이 아닌 경우) // 0 (x가 0인 경우)
-> 0은 1로, 1은 0으로 뒤집은 뒤 +1 해주면 음수가 된다. (모든 음수 코드는 1로 시작한다.)
2.2 명세
2.2.1 가산기
-
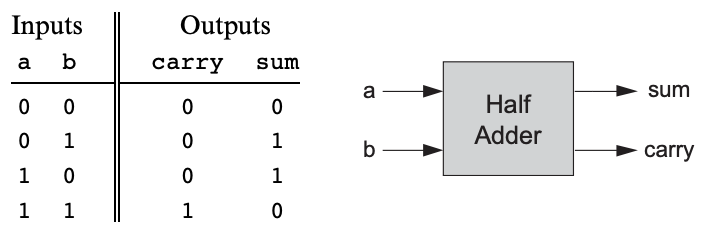
반가산기
두 비트를 더하는 기능을 한다. 덧셈한 값의 최하위 비트를 sum, 최상위 비트를 carry라 하자
-
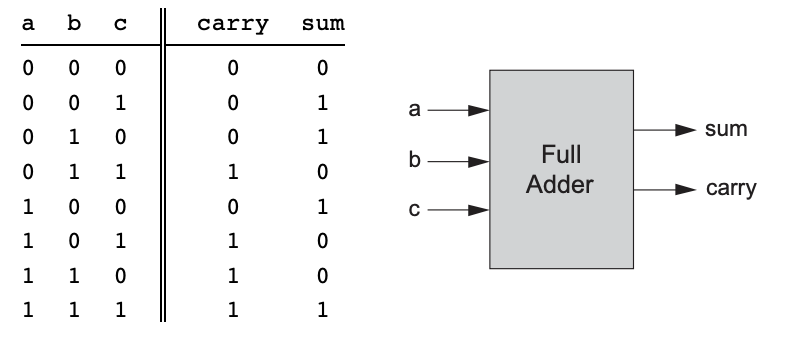
전가산기
세 개의 비트를 더하는 기능을 한다. 출력은 반가산기(sum, carry)와 같다.
-
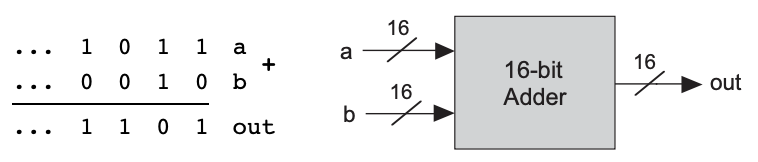
가산기
메모리와 레지스터 칩은 n비트 패턴으로 된 정수를 저장하고, n은 플랫폼에 따라 16, 32, 64 등등의 값이 된다. 이런 숫자를 덧셈하는 칩을 멀티비트 가산기 혹은, 가산기라 부른다.
-
증분기
주어진 숫자에 1을 더하는 기능을 한다.
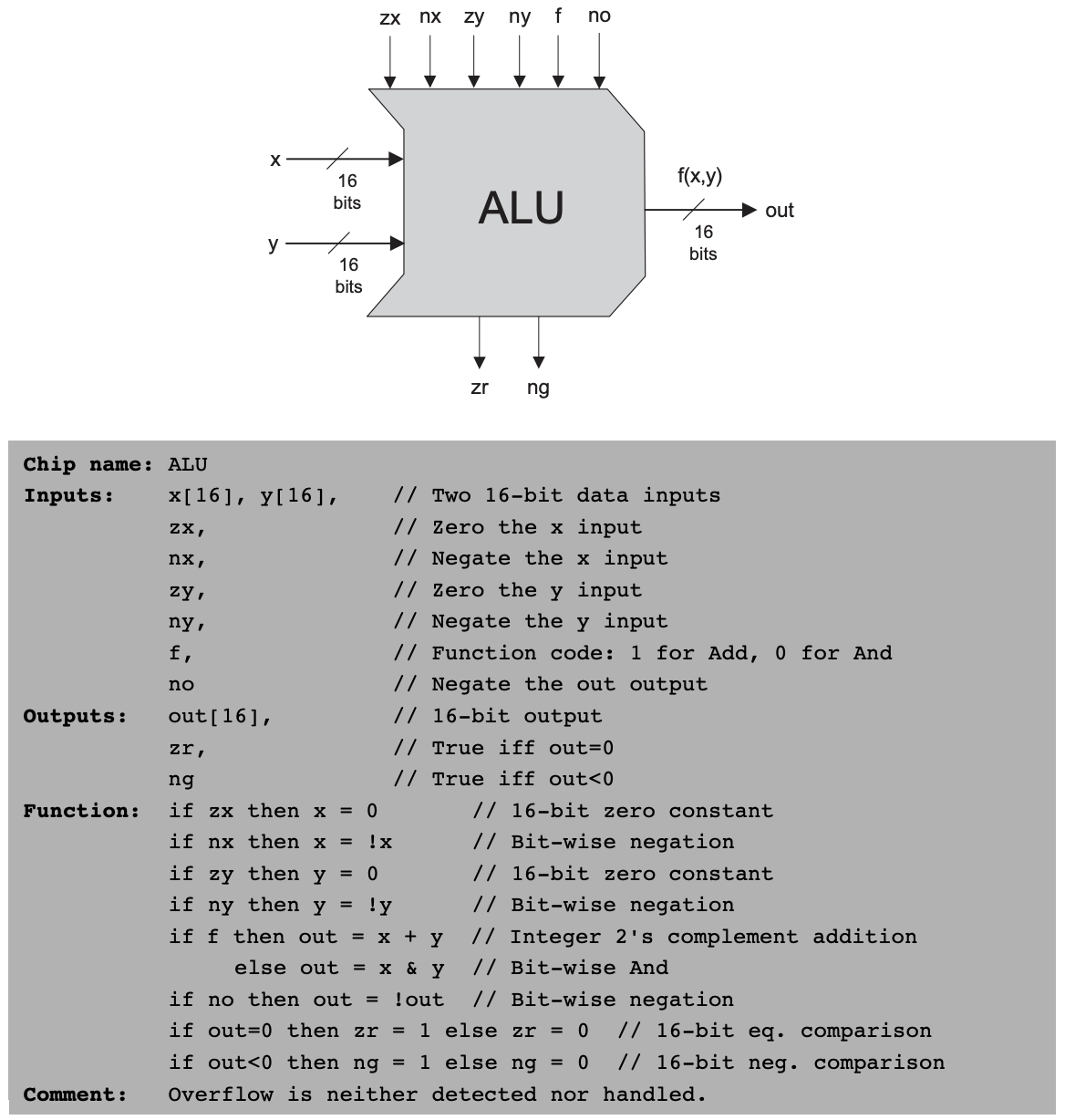
2.2.2 산술 논리 연산 장치(ALU)
핵 플랫폼의 ALU는 x와 y가 칩의 두 16비트 입력이고, 16비트 출력 값을 가진다.
주어진 2진 값들에 대해 ALU가 어떤 연산을 할지는 '제어 비트'라는 6개의 입력 비트를 통해서 결정한다.
2.3 구현
Half-Adder (반가산기)
위의 반가산기의 진리표를 보면 sum은 Xor과 같고, carry는 And와 같다는 것을 알 수 있다.
CHIP HalfAdder {
IN a, b; // 1-bit inputs
OUT sum, // Right bit of a + b
carry; // Left bit of a + b
PARTS:
// Put you code here:
And(a=a, b=b, out=carry);
Xor(a=a, b=b, out=sum);
}Full-Adder (전가산기)
전가산기의 sum 구현은 간단하다. 먼저 a와 b를 반가산기로 더한 sum을 c와 더하면 최종 sum을 구할 수 있다. 그리고 각각의 반가산기에서 발생한 carry를 Or 연산해줌으로 최종 carry값을 구한다.
CHIP FullAdder {
IN a, b, c; // 1-bit inputs
OUT sum, // Right bit of a + b + c
carry; // Left bit of a + b + c
PARTS:
HalfAdder(a=a, b=b, sum=sumAB, carry=carryAB);
HalfAdder(a=sumAB, b=c, sum=sum, carry=carrySumABSumC);
Or(a=carryAB, b=carrySumABSumC, out=carry);
}ALU(산술 및 논리 연산 장치)
ALU는 코드에 주석을 달아 놓았으니 주석을 참고하며 코드를 읽어보길 바란다.
CHIP ALU {
IN
x[16], y[16], // 16-bit inputs
zx, // zero the x input?
nx, // negate the x input?
zy, // zero the y input?
ny, // negate the y input?
f, // compute out = x + y (if 1) or x & y (if 0)
no; // negate the out output?
OUT
out[16], // 16-bit output
zr, // 1 if (out == 0), 0 otherwise
ng; // 1 if (out < 0), 0 otherwise
PARTS:
// Put you code here:
Mux16(a=x, b[0..15]=false, sel=zx, out=zX); // zx가 1이라면 x를 0으로 초기화한다.
Not16(in=zX, out=notZx);
Mux16(a=zX, b=notZx, sel=nx, out=znX); // nx가 1이라면 현시점의 x값을 반전시킨다.
Mux16(a=y, b[0..15]=false, sel=zy, out=zY); // zy가 1이라면 y를 0으로 초기화한다.
Not16(in=zY, out=notZy);
Mux16(a=zY, b=notZy, sel=ny, out=znY); // ny가 1이라면 현시점의 y값을 반전시킨다.
And16(a=znX, b=znY, out=andznXY);
Add16(a=znX, b=znY, out=addznXY);
Mux16(a=andznXY, b=addznXY, sel=f, out=fout); // f값으로 and, add 중 어떤 연산을 할지 결정한다.
Not16(in=fout, out=nfout);
Mux16(a=fout, b=nfout, sel=no, out[0..7]=out1, out[8..15]=out2, out[15]=ng, out=out); // no값이 1이면 결과값을 반전시킨다. 최종 출력값이 음수라면 ng를 1로 초기화한다.
Or8Way(in=out1, out=orOut1);
Or8Way(in=out2, out=orOut2);
Or(a=orOut1, b=orOut2, out=orOut); // 출력값을 앞, 뒤로 나누어서 or연산을 해, 1이 존재하는지 검사한다.
Not(in=orOut, out=zr); // or연산의 최종값에 따라서 zr을 결정한다.
}