ResNet

link: https://arxiv.org/pdf/1512.03385.pdf
CVPR 2016

Residual learning

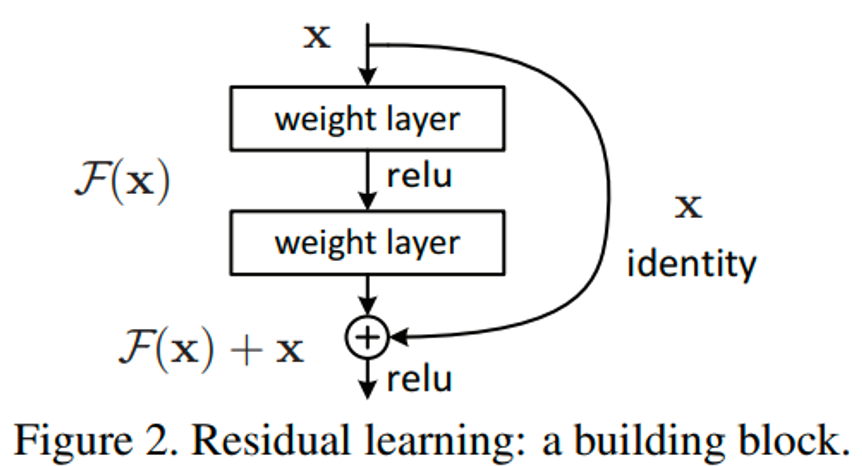
• 기존에는 H(x) = x 가 되도록 H 함수를 찾는 데 목표를 두었음
• 이 논문에서는 H(x) - x 를 새로운 함수 F로 정의 ⇒ F(x) = 0 이 될 수 있도록 F 함수를 찾는 것이 목표가 됨
• F: 예측값과 실제값의 차이인 잔차를 의미
• 이렇게 F가 0이 되는 방식으로 최적화 하는 것이 H를 찾는 것보다 좋은 성능을 냄
• H(x) = F(x) + x 로 다시 쓸 수 있음
  • H는 미분해도 x 때문에 1이 나옴 → 기울기 소실 방지
  • • x 부분을 shortcut connection 이라고 함
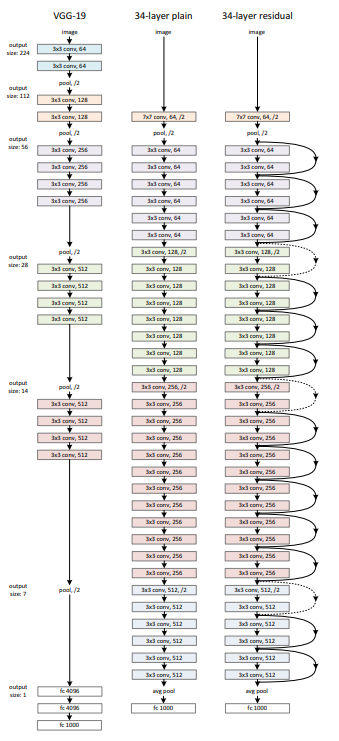
• 기본적인 모델은 VGG19에서 착안
• shortcut해서 elementwise하게 덧셈을 하려면 input ↔ output dim 같아야 함
  • 안되면? zero padding이나 linear projection

Bottleneck

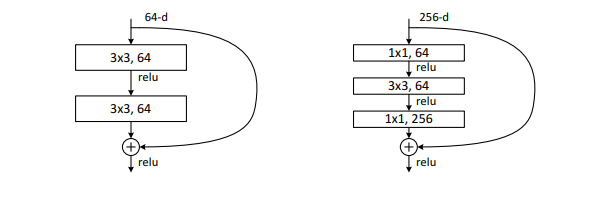
• 1*1 conv: channel 수 줄이기 위함
• resnet에서는 bottleneck 구조가 좋은 성능을 내진 못함

---

MobileNetV2

link: https://arxiv.org/abs/1801.04381
CVPR 2018

MobileNet V2

• SOTA 모델 컴퓨팅 성능이 높아 모바일, 임베디드에 적용이 불가
• ReLU activation의 비선형성 효과로 인해 정보(manifold)가 손실 → 채널 수 충분해야 정보 보존 가능

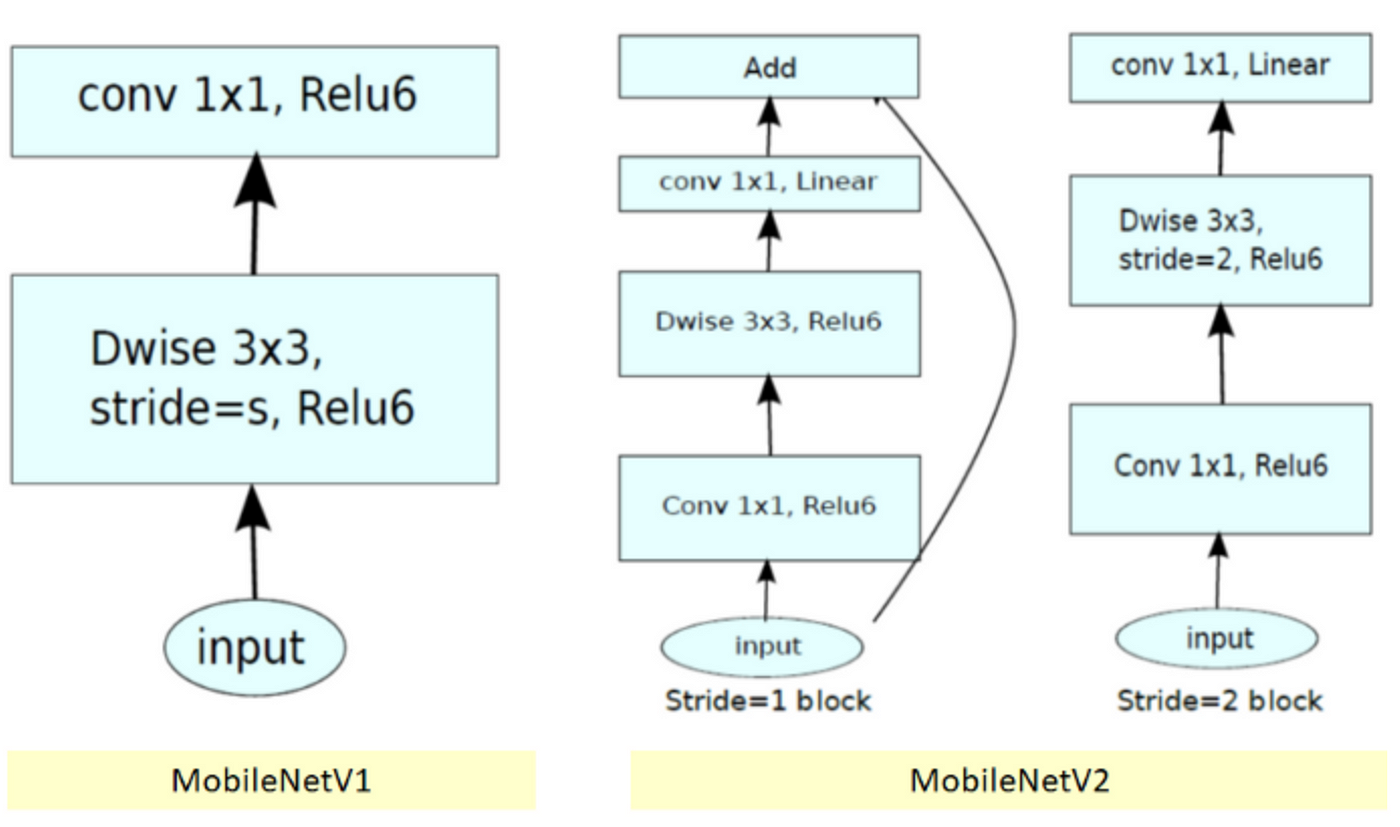
• V2에서는 stride 값에 따라 두 가지 블록으로 나뉘게 됨
• stride 1
  • inverted residual block에서 skip connection을 진행
• stride 2
  • 블록 구조는 stride 1과 동일하나 skip connection을 생략하고 Depthwise convolution에서 stride 2를 통한 downsampling을 진행

Linear Bottlenecks

• ReLU Activation은 채널 내의 정보를 불가피하게 손실
• 채널 내에서의 정보는 손실되나 여러 채널 사이에서 input manifold로부터 embedding된 정보(Manifold of interest)를 얻을 수 있음
• 낮은 차원으로 mapping할 때 하나의 채널에서 정보 손실되더라도 다른 채널에서는 손실된 정보가 살아있을 수 있기 때문에 정보가 보존됨

• 즉 linear transformation 역할을 하는 linear bottleneck layer를 활용해서 차원은 줄이되 manifold of interest를 그대로 유지하여 네트워크 크기는 줄어들지만 정확도는 유지하는 전략

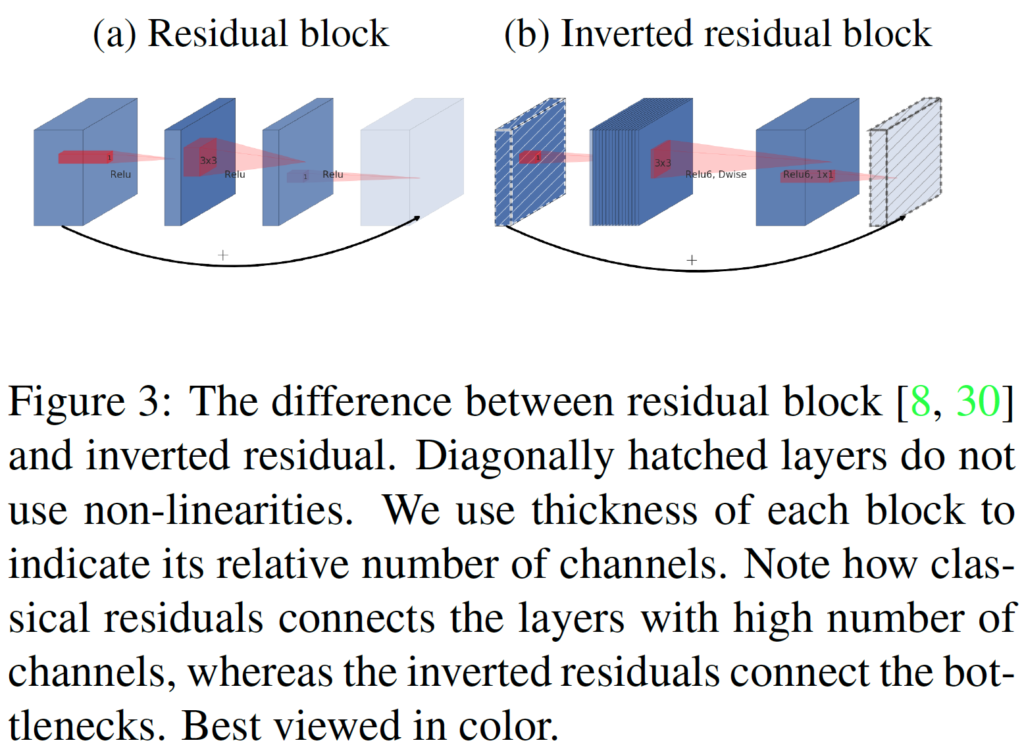
Inverted Residuals

• bottleneck 블록은 모든 입력이 bottleneck-expansion 뒤에 따라오는 형태의 residual block과 형태가 비슷
• 기존에 제안된 residual block에 linear bottleneck 형태를 붙인 형태
• inverted residual block은 input output 채널 수가 낮기 때문에 residual block보다 메모리 효율이 좋은 장점
• 연산량 비교: residual block vs inverted residual block
  • residual: h_i w_i d_i(k^2 + d_i)
  • inverted: h w d’ * t(d’ + k^2 + d”)
  • inverted residual block의 입력과 출력 채널 수가 더 적어 연산량 더 적음

---

EfficientNet

link: https://arxiv.org/abs/1905.11946
ICML 2019

summary

• 효율적인 모델 구축을 위해 depth, width, image resolution을 스케일링하는 방법 제안
  • 이전 연구에서는 셋 중 하나만 scale하는 것을 주로 다뤘음
  • 상수 비율로 세 가지를 각각 scaling하면 됨
• MnasNet에서 사용하는 conv 구조인 MBConv를 이용한 EfficientNet 제안

Compound Scaling Method

• width, depth, resolution을 fixed scaling coefficient로 균일하게 scale함

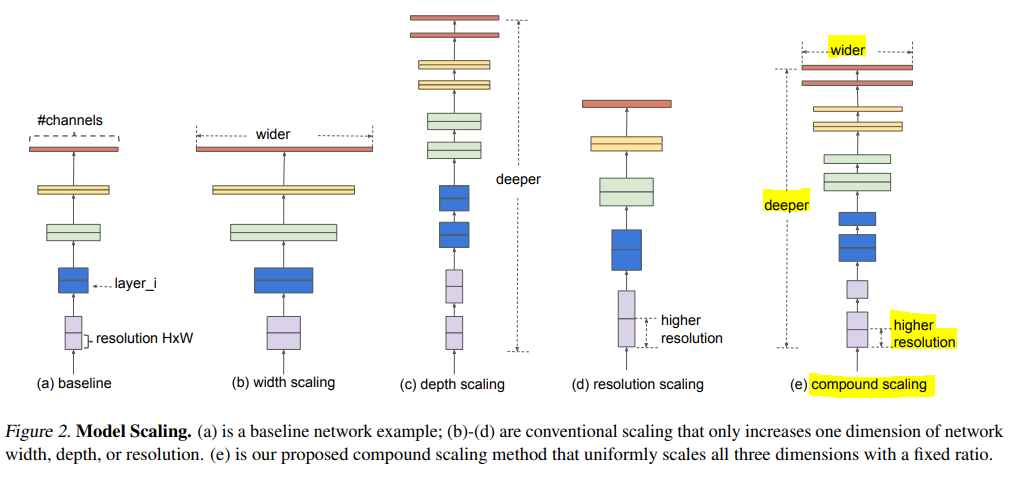
• 만약 2^N 만큼의 컴퓨터 자원을 더 사용할 수 있다면, depth를 α^N, width를 β^N, image size를 γ^N으로 증가시킴
  • 직관적으로 이미지가 크면 receptive field를 늘리기 위해 더 많은 layer가 필요하고, 더 미세한 pattern을 얻기 위해 더 많은 channel이 필요하기 때문
• model scaling의 효과는 baseline network에 따라 다름
  • baseline: neural architecture search 사용, model의 조합을 scale up 하여 EfficientNet 만듦

EfficientNet Architecture

• 처음부터 좋은 baseline network를 정하는 것이 중요함 → mobile-size의 baseline을 개발
• α, β, γ를 찾아 큰 모델에 적용하면 더 좋은 성능을 내는 것이 가능하지만, 큰 모델의 경우 이 값을 찾는 비용이 더 많이 들었음
  • 이 문제를 해결하기 위한 방법
    
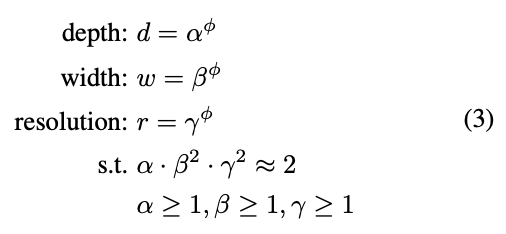
    • ϕ=1로 고정한 뒤 resource가 두 배로 있다고 가정하고 식3을 이용해 α, β, γ를 찾음
    • 또는 α, β, γ를 고정하고 ϕ값을 바꿔서 baseline network를 scale up 함

Conclusion

• width, depth, resolution 간 균형이 model을 scale up 하는 데 중요한 요소였음을 보임
• accuracy가 더 높고 효율적이면서, 쉽게 모델을 scale up 할 수 있는 방법을 제안
• 전이학습에서도 더 적은 prameter와 FLOP으로 잘 동작함을 보임