룽게-쿠타 방법(Runge–Kutta method)은
적분 방정식 중 초기값 문제를 푸는 방법 중 하나이다.
20세기 초, 독일의 수학자 카를 다비트 톨메 룽게와 마르틴 빌헬름 쿠타가
개발한 방법이다.
적분 방정식의 초기값 문제를 푸는 방법이라는 대목에서 알 수 있다시피
이는 수치적분에 관한 이론이며 계산할때, 주로 4차의 항까지만을 다루는
4차 룽게 쿠타 방법을 주로 사용한다. (약어로 주로 RK4 라고 표기함)
(더 정밀한 적분을 해야할 때는 6차 룽게 쿠타 방법 - RK6 을 사용함)
해당 방법의 유도는 다음과 같다. 우선, 시점 i 와 그 시점의
함숫값 y_i 가 있다고 하자. 그렇게 된다면, i+1 시점의 함숫값
y_i+1는 테일러 전개를 이용하여 다음과 같이 나타낼 수 있을 것이다.
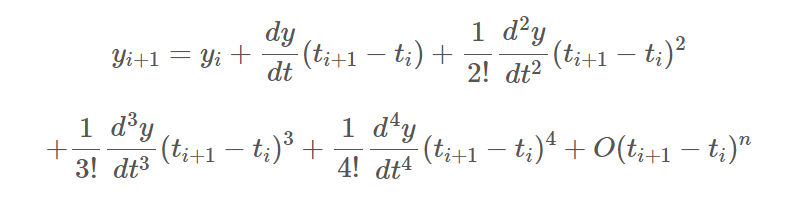
특히 여기서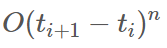 
항은 n 차의 오류항으로, n차 이상의 테일러 전개식은 오류로 처리한다.
우리가 진행하는 것은 4차 룽게-쿠타 방법으로, 5차 이상의 항을들 전부 오류로 묶어
하나의 식으로 정리하자. (대부분의 자연현상에서, 4차이상의 변수들에 대해서는
대게 선형적인 모습을 띄고 있어, 이러한 방식이 수치해석 과정에서의 효율성과
그 범용성을 높여 준다.)
위의 오류항이 충분히 작아 무시 가능하면, 함숫값 y_i+1은 다음과 같이 사용할 수 있다.
(h: 각 구간 사이의 길이) (구간으로 나누는 이유는 이전 포스트 '수치미분과 수치적분' 참고)
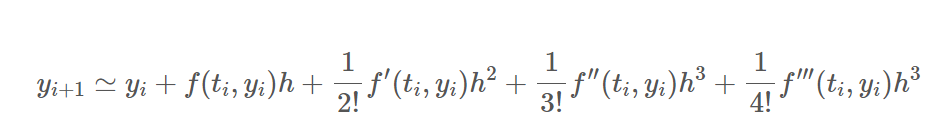
여기서 f(t_i, y_i) 의 경우, 특정 시점 i 에서의 y의 변화, 즉 y'_i을 다른 방식으로 표현한 것이다.
그리고 여기서 룽게 쿠타 방법 에서의 일종의 '정의' 가 있는데 바로 다음 식이다.
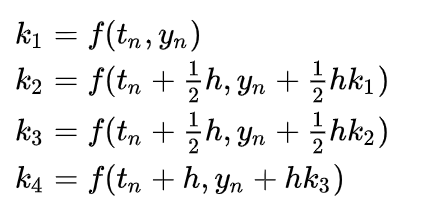
다음 식에서의 의미는 다음과 같다.
k1 : 특정 구간의 시작 부분 n 에서의 기울기에 의한 증분
k2 & k3: 특정 구간의 중간 부분의 기울기에 의한 증분
k4: 특정 구간의 끝 부분에서의 기울기에 의한 증분
해당 식들은 룽게 쿠타 방법에서의 중요한 의미를 지니며, 최종적으로 유도된 식에서도
해당 식들이 포함된 상태로 유도 된다.
여기서 룽게 쿠타 방법의 개념을 이해할 수 있는데, 룽게 쿠타 방법은
각각 네부분의 기울기를 특정한 방법으로 통계를 내어 특정 구간 다음의 함숫값을
수치적으로 계산하는 방법이다. 따라서 각 구간에서의 기울기와 관련한 식들은
큰 의미를 지닌다.
위에서 소개했던 개념에 따라 룽게 쿠타 방법의 기본 형태를 나타내어 주면,
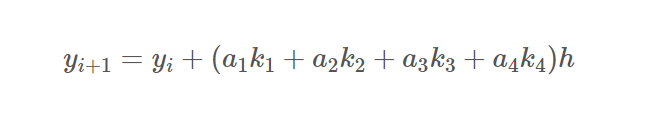
다음과 같이 나타낼 수 있다.
해당 식이 위에서의 테일러 전개의 식과 맞아야 하므로 전개하여 정리해주면,
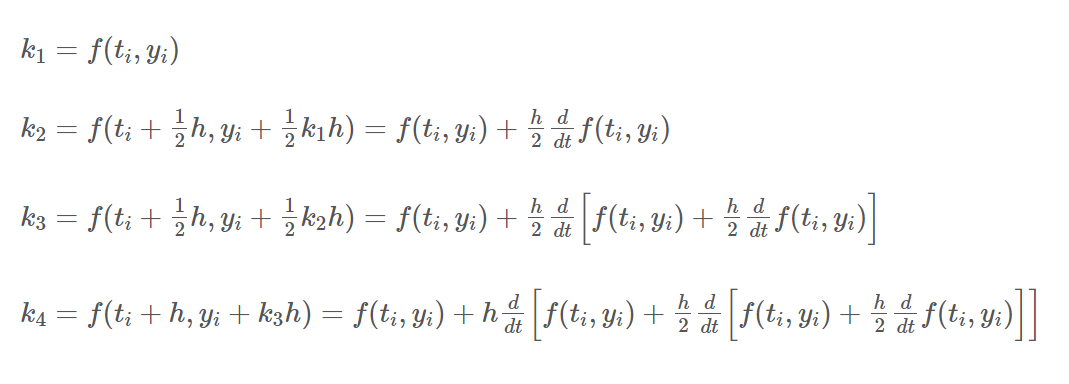
k를 확장하여 정리하였으니 해당 식을 기본 형태에 대입하여 주면,
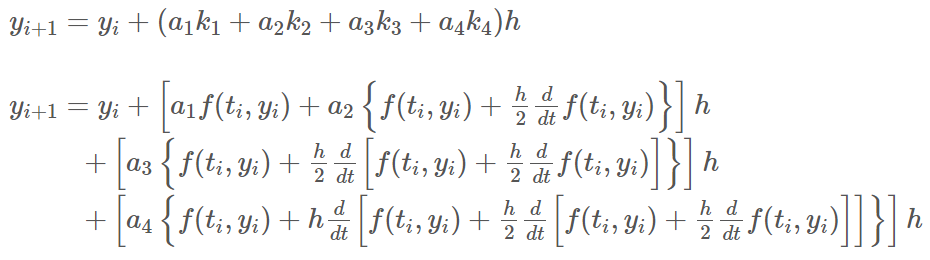
따라서 정리하면 다음과 같은 식이 나온다.
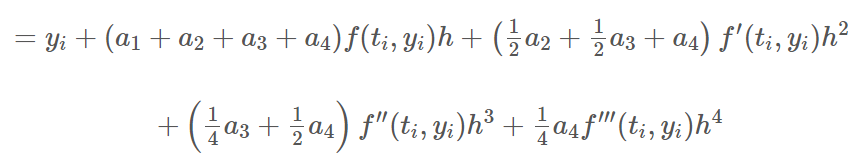
여기에서 앞서 설명하였던 테일러 급수를 이용한 전개와 계수를 비교해준다.
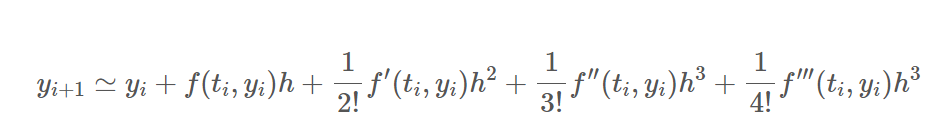
위의 두 식을 연립하여 a1~a4 를 확정하여 주면, 최종적으로 다음과 같이 표현된다.
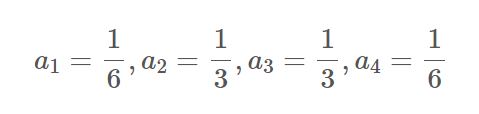
이를 룽게 쿠타 방법의 기본 형태의 식에 대입하여 주면 결과적으로 다음 식을 얻을 수 있다.
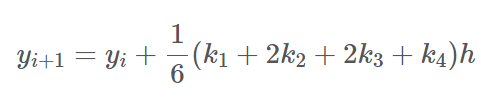
이 방법을 이용하여 다른 구간의 해를 수치적으로 구해내어 미분 방정식의 해를
수치적으로 구해낼 수 있다.
