Python을 이용하여 '장' (Field)을 표현해보자
오늘은 Python (Google colaboratary)를 이용해서 '장(Field)'를 나타내 볼까 한다.
우선 '장(Field)' 이란 무엇일까?
물리학에서 말하는 '장(Field)' 이란,
공간상의 각 지점마다 다른 값을 갖는 물리량을 일컫는 용어이다.
쉽게 말해 공간상에 위치에 대한 '특정한 물리량'의 함수이다.
예를 들어, 위치에 따라 다른 크기의 자기력이 형성되는 자기장과
중력을 가진 물체 때문에 위치에 따라 다른 크기의 중력이 형성되는 중력장이 있다.
그렇다면 이런 장은 어떻게 수학적으로 나타날까?
그것을 이해하기 위해서는 먼저, 장의 종류를 알아야한다.
장에는 위치에 대한 값이 스칼라 (크기만을 갖는 특정한 양) 으로 나타나는 '스칼라장'과
그 값이 벡터 (크기와 방향을 가짐) 로 나타나는 '벡터장' 이 있다.
우선 스칼라장은 어떻게 표현할까?
2차원의 스칼라장 S 가 있다고 하자.
(앞으로 모든 좌표의 표현은 x-y 2차원 직교좌표계가 기준이 됨)
이때, 이 스칼라장은 다음과 같이 나타낼 수 있다.
S(x,y) = x^2+ xy +y^2 (예시)
스칼라장을 표현 할땐, 다음과 같이 간단히 x,y에 대한 함수로써 나타내주면 된다.
그렇다면, 각각의 (x,y) 좌표에 대응하는 스칼라의 양이 나올 것이다.
그렇다면 벡터장은 어떻게 표현할까?
우리는 먼저, 벡터가 어떻게 표현되는지를 알아야한다.
먼저 벡터가 분해될 수 있다는 것을 안다고 가정하고 설명하자면,
(벡터는 합성 및 분해 될 수 있음, 아래 그림 참조)
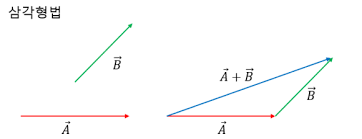
출처: 네이버 블로그, Gtryur - 벡터의 합과 절댓값
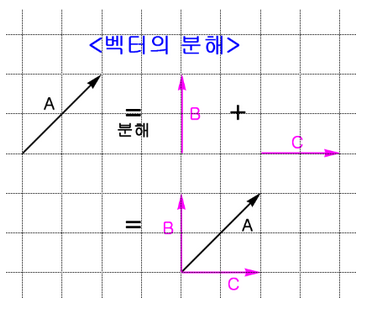
https://develop88.tistory.com/entry/%EB%B2%A1%ED%84%B0%EB%B6%84%ED%95%B4
두번째 그림에서 볼 수 있듯이, 직교좌표계에서는 각각의 축의 성분으로
벡터를 분해시킬 수 있다. 따라서 각 축을 대표하는 방향을 가진 '단위 벡터'에
각각의 축 성분의 크기를 곱해서 모든 벡터를 나타낼 수 있다.
(보통 x축 방향 단위 벡터를 i, y축 방향 단위 벡터를 j, z축 방향 단위벡터를 k라 한다.)
예시
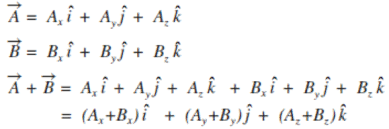
http://www.astronomer.rocks/news/articleView.html?idxno=82915
(단위 벡터의 크기는 1임)
즉 모든 벡터를 단위벡터와 그 축에 해당하는 '성분'으로 나타낼 수 있다는 말인데,
벡터장의 결과값 역시 벡터이고, 단지 위치에 대한 함수일 뿐이니
벡터장을 표현하는 것이 그렇게 어렵지 않은 것 같다.
(아래에 2차원 벡터장 V 표현)
V(x,y) = P(x,y) i + Q(x,y) j
원래 벡터를 표현하는 방식과 마찬가지로 벡터장을 성분과 각 성분의 단위 벡터로 쪼개는데,
이때 이 '성분' 이 되는 함수 P(x,y) , Q(x,y) 를
성분함수 (component function) 라고 한다.
이제 스칼라장과 벡터장의 개념에 대해 알았으니,
어떻게 Python 언어에서 개발하는지에 대하여 알아보자
우선 numpy 라이브러리와 matplotlib 라이브러리를 이용해야한다.
numpy와 matplotlib은 다양한 수학적 기호들과 장을 그릴 수 있게 해주는 기능들을 제공한다.
저번 '수치미분과 수치적분' 편에서도 설명했다시피 우리의 컴퓨터는
연속적인 (끊어지는 부분이 없는) 연산을 할 수가 없다.
따라서 이 '장' 을 표현하는 방식도 연속적인 공간상의 위치가 아닌, 위치가 일정한 간격으로 '잘 끊어진' 공간을 만들어 그곳에 시각화 해야한다.
따라서 우리는 'linspace' 함수와 'meshigrid' 함수를 이용하여
'일정한 간격으로 잘 끊어진' 2차원 배열을 만들 것이다.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 1000)
y = np.linspace(-1, 1, 1000)
X, Y = np.meshgrid(x, y)- linspace 사용법 : linspace(시작값,끝값,사이를 나눌 간격)의 형태로 사용함
그리고 스칼라장이 될 변수 'S' 를 선언한다.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 1000)
y = np.linspace(-1, 1, 1000)
X, Y = np.meshgrid(x, y)
S = X**2 + Y**2 (ex)위치에 대한 각각의 스칼라의 크기를 전부 나타낼 것이기 때문에,
변수 'S' 내에는 x,y 가 아닌 X,Y 를 집어넣어 선언한다.
이제 스칼라장을 표현해보자.
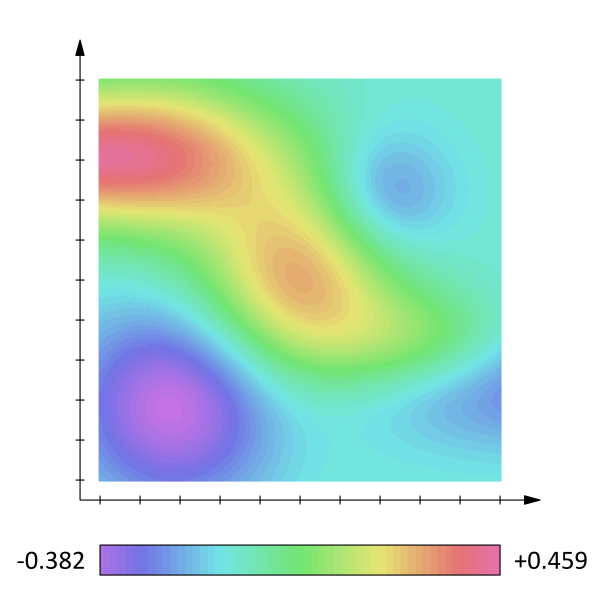
보통의 스칼라장(온도 같은 경우)을 표현할때에는 아래의 그림과 같이
색으로 표현하는 경우가 많다.
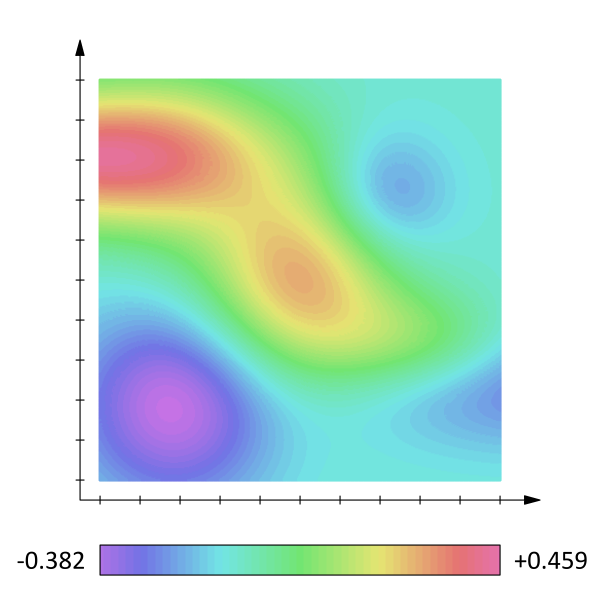
출처 : wikipedia
보통 스칼라의 크기에 따라 빨간색이나 보라 색등 다양한 색을 사용하는데,
이 포스트에서도 마찬가지로 스칼라 장을 색으로 표현하고자 한다.
(사실 일반적으로도 색으로 표현하고, 그것이 훨씬 퀄리티가 좋다.)
각각의 위치 (좌표) 에 대응되는 스칼라의 크기에 따라 색을 나눠 표현하면,
스칼라장을 위의 그림 처럼 나타낼 수 있을 것이다.
따라서 크기에 따라 색을 조절할 수 있는 '컬러맵'을 이용하여
스칼라장을 나타내보자.
컬러맵에는 다양한 종류가 있는데, 우리는 그 중에 'viridis' 컬러맵을 이용할 것이다.
plt.cm.viridis 이용,
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 1000)
y = np.linspace(-1, 1, 1000)
X, Y = np.meshgrid(x, y)
S = X**2 + Y**2 (ex)
plt.cm.viridis(S)그 이후 출력을 나타내는 'plt.imshow' 와
색에 따른 스칼라의 크기비교를 위한 'plt.colorbar(label='Scalar Value')' 를
추가하고, (색깔을 막대의 형태로 출력) 이제 전체적인 그래프를 출력해보자
전체코드
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 1000)
y = np.linspace(-1, 1, 1000)
X, Y = np.meshgrid(x, y)
S = X**2 + Y**2
plt.cm.viridis(S)
plt.imshow(color, extent=(-1, 1, -1, 1)) #
plt.colorbar(label='Scalar Value')
plt.xlabel('X')
plt.ylabel('Y')
plt.axis('equal')
plt.show()참고: plt.imshow 사용양식
plt.imshow(표시할 데이터, 컬러맵, 가로세로 비율, 출력될 범위, 투명도,)
출력 결과
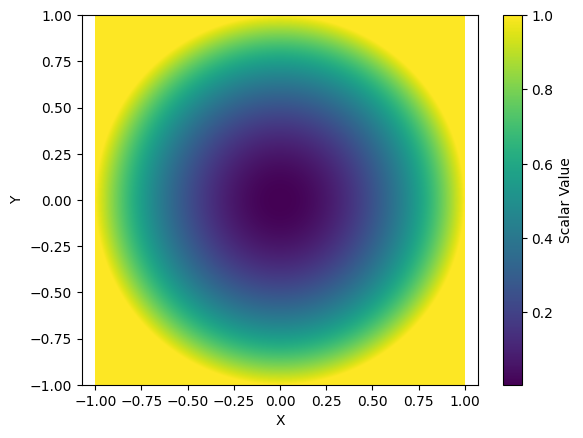
이렇게 효과적으로 스칼라장을 표현할 수 있다.
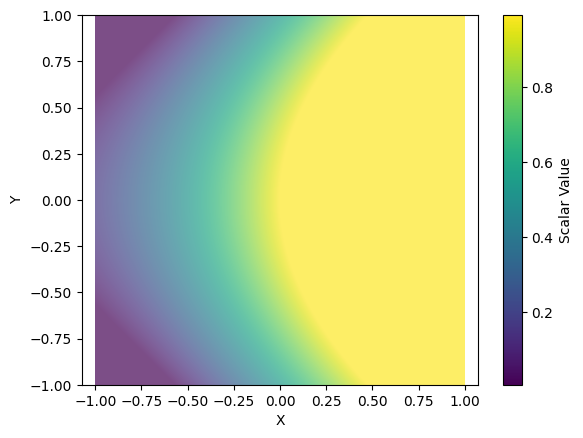
예시 S = sinx+cosy
S = exp(x)+y
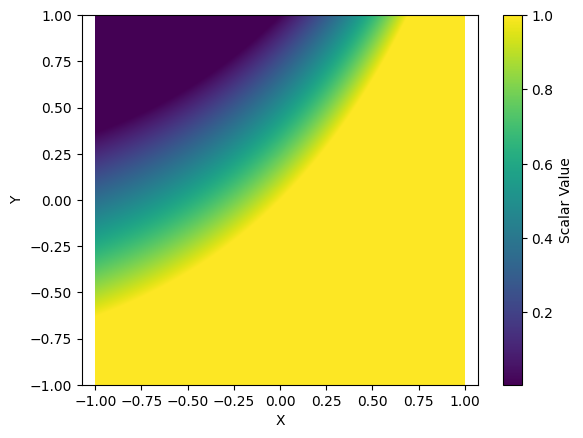
(상당히 예쁘다)
이제 벡터장을 표현해보자........
사실 기본적인 표현방법은 일전에 이미 다 설명했다.
공간 선언하기, 표현하기, 색깔 집어넣기 등
전체적인 표현방식은 거의 유사하다.
그러나 벡터장을 표현하기 위해서는 완벽히 같은 방법으로 표현할 수는 없다.
그전에, 벡터에 관한 그림이나 사진을 보았을때, 벡터를 과연 어떻게 표현하던가?
그렇다. 바로 '화살표'로 표시했다.
따라서 벡터장도 위치에따라 각기다른 방향과 크기를 가진 화살표로 표현한다면,
벡터장을 효과적으로 표현할 수 있는 것이다.
그리고 수학적으로 벡터장을 표기하는 방법은 방금전에 제시하였다.
V(x,y) = P(x,y) i + Q(x,y) j
그리고 이러한 화살표 를 표현할 수 있는 함수가 matplotlib에 내장되어있다.
바로 'plt.quiver'이다.
밑에는 plt.quiver 사용양식이다.
plt.quiver(X,Y, X 방향의 벡터 성분,Y 방향의 벡터 성분,화살표 크기, 색상, ...)
여기서도 벡터의 크기에따라 색을 다르게 표현할 것이다.
벡터의 크기를 나타내는 방식은 아래의 그림이 이해를 도울것이다.

아래에는 V(x,y) = sin(pix) i+ cos(piy) j의 벡터장을 나타내는 코드이다.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 20)
y = np.linspace(-1, 1, 20)
X, Y = np.meshgrid(x, y)
def V_component_x_function(x, y):
return np.sin(np.pi * x)
def V_component_y_function(x, y):
return np.cos(np.pi * y)
V_component_x = V_component_x_function(X, Y)
V_component_y = V_component_y_function(X, Y)
vector_magnitude = np.sqrt(V_component_x**2 + V_component_y**2)
color = vector_magnitude
plt.quiver(X, Y, V_component_x, V_component_y, color, cmap='viridis')
plt.colorbar(label='Vector Magnitude')
plt.xlabel('X')
plt.ylabel('Y')
plt.axis('equal')
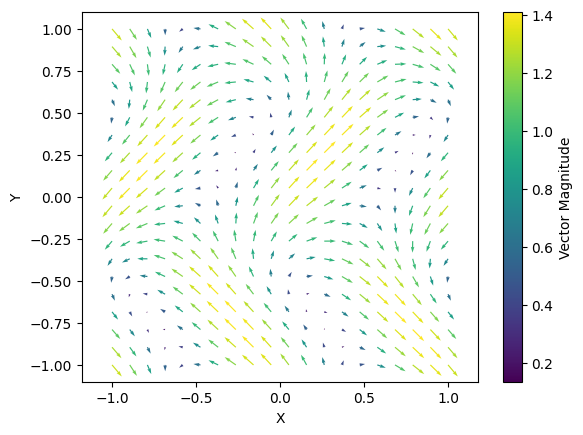
plt.show()출력결과

예시 V = sin(pix - cos (piy)) i + cos(pix - sin (piy))
그렇다면, 우리는 어째서 '장'을 시각화 해야하는 걸까?
사실 이 '장' 은 기상학,온도 분포,전압 분포등 다양한 상황에서 많이 쓰인다.
그것을 한눈에 볼 수 있는 그래프로써 나타낸다는 것은 많은 물리학적이고
현실의 문제상황을 쉽게 이해할 수 있게 도와준다.
또, 우리가 수식을 실제 그래프로 바꾸기도 하고 실제 데이터를 식으로 바꿀 때에도
장을 시각화 하는 것은 엄청난 도움이 된다.
또한, 장으로써 쉽게말해 위치에 대한 함수로써 나타낼 수 있다면, 우리는 실제 그 위치에 있지 않더라도, 그곳에서의 물리량을 예측할 수 있게된다.
이렇게 오늘은 벡터장과 스칼라장을 표현하는 방법을 알아보았다.
참! 잘했어요!