우리의 컴퓨터는 매우 뛰어나다.
인간 보다 훨씬 더 많은 양의 연산을 눈 깜짝할 새에 풀어내는 것을 많이 보았을 것이다.
우리 컴퓨터의 연산속도는 초당 약 1억번 정도이다.
1초에 약 1억번의 계산을 하거나 또는 판단을 내릴 수 있다는 것이다.
이런한 점 때문에, 우리가 컴퓨터로 문제를 해결 할때, 언제나 순식간에 답이 나오는 것은 어찌보면 당연한 사실이다.
그렇다면 다음 문제를 풀어보자
"피보나치 수열의 100번째 항을 구하라"
*피보나치 수열: 첫째 및 둘째 항이 1이고 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열
우린 피보나치 수열의 정의를 이용하여 다음과 같은 함수를 만들어 해결 할 수 있을 것 같다.
Fibonacci (int n)
{
if(n == 0) return 1;
else if(n == 1) return 1;
else return Fibonacci(n-1) + Fibonacci(n-2)
}
그렇다면 해당 함수를 이용하여 피보나치 수열의 100번째 항을 "눈 깜짝할 새"에 풀어보자
아마도 안될 것이다. 눈 깜짝할 새가 아니라 아마 당신이 눈을 감는 그 순간에도
컴퓨터는 계속 연산을 해야할 것이다.
왜냐고? 해당 코드를 수형도로 그려보자
아마도 다음과 같은 그림이 그려질 것이다.
위 알고리즘의 시간복잡도는 O(2^n) 이다.
알고리즘으로 문제를 푸는데에 n의 값이 늘어날 수록 연산횟수는 2의 지수꼴로 늘어난다.
그러니 당신이 눈을 감을때까지 컴퓨터가 연산을 하고 있다는 말은 과언이 아니다.
연산의 횟수는 약 2^100 = 1,267,650,600,228,229,401,496,703,205,376 회
컴퓨터가 초당 100,000,000 번 연산 가능하니 그 어떤 시간과도 비교 하기 어려울 정도로 까마득한 시간이 소요 될 것이다.
방금 나의 말이 잘 이해 되지 않을 수 있다.
어찌 보면 당연하다. 처음 듣는 용어를 사용하고 (O,시간복잡도...)
갑자기 엄청나게 큰 수 를 제시 했으니깐 말이다.
그러나 이 개념은 프로그래밍을 함에 있어 엄청나게 중요하다.
조금 더 나은 방향으로 문제를 풀어낼 수도 있고,
알고리즘의 효율을 압도적으로 늘려주기도 한다.
이 개념의 이름은 앞서 말했다시피 "시간복잡도" 이다.
지금 부터 나와 함께 이 "시간복잡도'에 대해서 알아보자
짜잔! 여기에 맛있는 삼각김밥이 있습니다!
아주 아주 배가 고픈 당신은 어서 빨리 먹고 싶겠죠?
그러나 조건이 있습니다.
삼각김밥의 길이를 알 때, 몇개의 삼각김밥이 만들어 질 수 있는지 맞춰야 합니다!
갑자기 무슨 삼각김밥이냐고 물을 수도 있다.
그러나 어쩔 수 없다. 우리는 인간이기 때문에 배가고프면 그 어떤 것도 할 수 없다.
그러니 일단 문제를 풀고 삼각김밥을 먹자.
그렇다면, 어떻게 이 문제를 해결 할 수 있을까?
'만들어 질 수 있는 삼각김밥' 의 개수는 '만들어 질 수 있는 삼각형' 의 개수와 같다.
그렇다면, 간단하게 삼각형의 결정조건을 이용하여 문제를 해결 할 수 있다.
#include<stdio.h>
int N;
int cnt;
int main()
{
scanf("%d", &N);
for(int i=1; i<=N; i++)
{
for(int j=1; j<=i; j++)
{
for(int k=1; k<=j; k++)
{
if(i+j+k==N and i<j+k) cnt++;
}
}
}
printf("%d", cnt);
}
이렇게 '만들어질 수 있는 삼각김밥' 의 개수를 알 수 있다.
하지만 고약한 출제자가 변의 길이를 10000000으로 줬다고 생각해보자.
배가 아주 아주 고픈 우리들은 한 시라도 빨리 삼각김밥을 먹고 싶다.
그렇게 생각했을때, 해당 코드로 10000000의 변의 길이로
문제를 풀면 엄청나게 오랜 시간이 걸린다.
일단 3개의 반복문이 실행되며 각각 10000000번 연산해야 하므로 연산횟수는
어림잡아 약 10000000의 3제곱이 될 것이다.
그렇다면 조금 더 효율적인 방법은 없을까?
머리가 좋다면 다음과 같은 생각을 할 수 있다.
"마지막 변 (k) 의 값까지 반복문을 실행시킬 필요가 있나?"
그렇다. 앞선 두개의 변의 값이 정해진다면, 나머지 한 변의 길이는 자동으로 정해진다.
다음의 사실을 이용하여, 코드를 수정한다면, 다음과 같다.
#include<stdio.h>
int N;
int cnt;
int main()
{
scanf("%d", &N);
for(int i=1; i<=N; i++)
{
for(int j=1; j<=i; j++)
{
int k = N-i-j;
if(k<=j&&i<j+k) cnt ++;
}
}
printf("%d", cnt);
}그렇다면, 이 코드의 연산횟수는 얼마나 될까?
2개의 반복문이 실행되며 각각 10000000 번 연산하니 총 연산횟수는
10000000의 제곱이 될 것이다. 아직까지도 굉장히 큰 수이긴 하지만,
이전의 코드보다는 획기적으로 줄어들었다.
정보과학에서 이러한 문제 해결에 걸리는 시간과 입력간의 함수관계를
"시간복잡도" 라고 한다. 표기는 Big-O 표기법이라고 불리는 표기를 사용하는데,
O(N) 와 같이 표기하며 "입력에 대하여 알고리즘이 가질 수 있는 시간복잡도의 상한선" 이라는 의미를 가지고 있다.
(Big-O 는 상한선을 의미하고, Big-Omega는 시간복잡도의 하한선을 의미한다.)
Big-O 표기법을 이용하였을때, 방금 작성한 코드는 O(N^2)의 시간복잡도를,
그 이전에 작성한 코드는 O(N^3)의 시간복잡도를 가지고 있다고 설명할 수 있다.
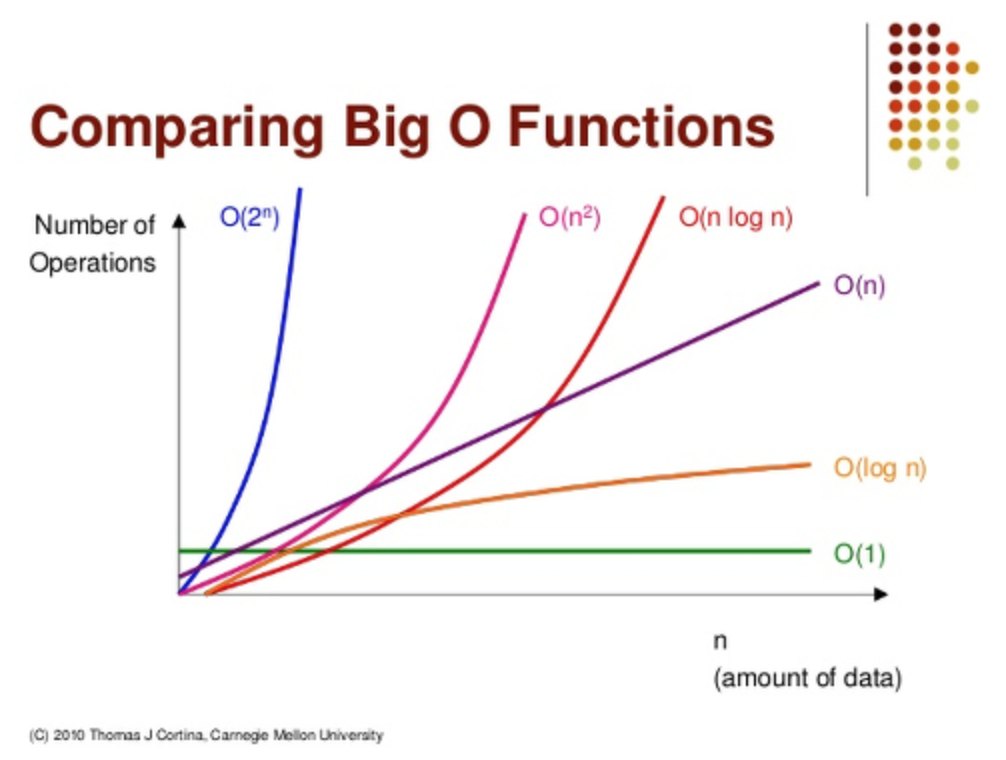
해당 사진은 Big-O 표기법으로 나타내었을때,
데이터의 양에대한 연산의 횟수를 나타낸 그래프이다.
그래프의 기울기가 클 수록 적은 데이터 양으로도 많은 연산이 필요하다는 의미이므로,
더 비효율적인 알고리즘이라고 할 수 있다.
그렇다면 위의 그 '삼각김밥' 문제를 더 효율적으로 해결할 수 있을까?
문제를 더 효율적으로 해결하는 과정은 변수나 범위같은 것들을 점점 줄여나가는 것이다.
이를 "탐색공간의 배제" 라고 하는데, 이 방식을 이용하여 위 문제를
O(N)의 시간복잡도로 해결해보자.
먼저 가장 긴변의 범위를 제한 해보자, 삼각형의 결정 조건에 따라
가장 긴 변의 합이 나머지 두 변의 합보다 작아야 한다.
따라서 가장 긴 변은 주어진 변의 길이의 절반을 넘을 수 없다.
그리고 또한 '가장' 긴 변이어야 하므로 주어진 변의 길이의 1/3 보다 작아선 안된다.
두번째로 긴 변의 (second) 길이의 범위를 생각해보자
아마도 최대값은 가장 긴 변일 것이다.
가장 작은값은 주어진 변의 길이에 가장 긴 변의 길이를 뺀 값에 절반 이상이어야 할 것이다.
그렇게 되면 두번째로 긴 변의 개수를 구할 수 있는데,
이는 두 정수 사이의 정수의 개수를 세는 공식과 일치한다.
(최대) - (최소) + 1
이를 이용하여 코드를 작성하면,
#include <stdio.h>
#define lint long long int // 더 큰 숫자를 처리하기 위한 입력 범위 확대
lint N;
lint cnt;
int main()
{
scanf("%lld", &N);
for(lint i=(N+2)/3; i<=(N-1)/2; i++)
{
cnt += (i-(N-i+1)/2+1);
}
printf("%lld", cnt); }다음과 같은 코드가 될 것이다.
i=(N+2)/3
i<=(N-1)/2
(i-(N-i+1)/2+1) 와 같은 식들을 보고 단번에 이해하긴 힘들 수 있다.
그러나 그 뜻을 풀어보면 이건 단순히 3의 배수, 짝수와 홀수를 나누는 식이라고 볼 수 있다.
만약 N의 값이 3으로 나눈 나머지가 1인 수 (ex 4) 라고 해보자.
만약에 그렇다면, i 의 최소값은 N/3+1 (ex 2) 가 될 것이다.
나머지가 2인 수 역시 N/3+1 과 같이 출력되고,
i<=(N-1)/2
(i-(N-i+1)/2+1) 해당 두 식의 의미도 N이 짝수냐 홀수냐에 따라 나와야 하는 값을
단지 일반화 한 식이라는 것을 알 수 있다.
이렇게 O(N)의 방식으로도 해당 문제를 해결 할 수 있었다.
어떤가? 처음의 풀이와 비교했을때, 훨씬 더 빠른 시간안에 문제를 풀고
삼각김밥을 먹을 수 있다.
하지만, 방금 우리의 풀이를 본 문제의 출제자가 약이 바짝 올랐는지,
갑자기 터무니 없이 큰 숫자 (ex 1000000000000000) 와 같은 수를 줬다고 생각해보자.
이 숫자는 이전의 그 코드 ( O(N) )의 코드로 시도하여도 상당한 시간이 걸리는 숫자이다.
그렇다면 어떻게 할까?
방금 시간 복잡도를 설명하기 위한 사진을 본 사람들이라면 우리가 아직 2가지의 방식을 다루지 않았다라는 것을 눈치챌 수 있을 것이다.
바로 O(1), O(logN) 방식이다.
그 중에서도 O(1) ( 상수 시간복잡도: 입력되는 데이터의 크기와 상관 없이 항상 일정한 시간 안에 문제를 해결함 ) 으로 문제를 해결해보자.
그렇다면 우리가 또 무엇을 배제할 수 있는지를 생각해봐야한다.
O(N) 코드의 반복문 안을 보자 해당 코드의 의미는
'cnt' 에 N의 값에 따른 i의 최소값부터 최대값까지 더한다는 것이다.
이렇게 반복해서 더하는 것을 반복문을 사용하지 않고 해결 할 수 있을까?
가능하다. '가우스'가 만들었다고 알려진 '연속된 자연수의 합' 공식을 이용하면, 반복해서 더하지 않아도 한번에 그 합을 유도해낼 수 있다.
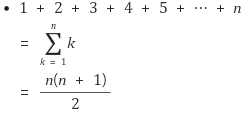( 연속된 자연수의 합 공식이다. )
그러나 우리는 최소값부터 최대값까지 더해야하므로 '1 ~ 최대값 까지의 합'에서
'1 ~ 최소값-1 까지의 합' 을 빼주어야 한다.
또한 (N-i-1)/2 의 반복된 합을 고려해 준다면, 해당 값은 2로 나누어준 값이기 때문에,
동일 한 값이 따로 2번씩 더해진다. 따라서 (N-max-1)/2 ~ (N-min-1)/2의 누적합의 2배를 해줘야 하는데, 경계값 (최대 또는 최소)에서 불필요한 값이
1번씩 더 더해질 수 있기 때문에, 이를 고려 해줘야 한다.
그렇다면 언제 이런일이 생길까?
바로 (N-min-1)이 짝수 또는 (N-max-1)이 홀수일때, 1번씩 추가로 더해진다.
따라서 이것을 고려하여 코드로 나타내 줘야 한다.
#include <stdio.h>
#define lint long long int
lint N, min, max;
lint tmp, ans;
lint sum(lint k)
{
if(k%2==0) return k/2*(k+1);
else return (k+1)/2*k;
}
int main()
{
scanf("%lld", &N);
min = (N+2)/3;
max = (N-1)/2;
if(min > max)
printf("%lld", ans);
else
{
// 1. (N-i-1)/2 모두 더한 값 구하기
// [(N-max-1)/2, (N-min-1)/2]
tmp = ( sum((N-min-1)/2) - sum((N-max-1)/2-1) )*2;
// 중복으로 계산된 (N-i-1)/2 값 제외하기
if((N-max-1)%2 == 1) tmp -= (N-max-1)/2;
if((N-min-1)%2 == 0) tmp -= (N-min-1)/2;
// 2. i - (N-i-1)/2 모두 더한 값 구하기
ans = sum(max) - sum(min-1) - tmp;
printf("%lld", ans);
}
}위의 자연수의 합 공식에서 홀 짝에 대하여 식이 다르게 나타나는 것처럼 보이는데,
이는 자연수의 합 공식을 적용하는 과정에서 곱셈이 사용되는데, 이때 일어날 수 있는
'오버플로우 (overflow)' 를 미리 예방하기 위함이다.
이렇게 드디어 우리는 삼각김밥을 먹을 수 있게 되었다!!
그럼 이제 맛있는 삼각김밥도 먹었고 배도 찼으니
마지막으로 O(logN) 을 가지는 알고리즘을 알아보자.
그 전에 O(logN) 에 대해서 먼저 알아보자면 O(logN)은 Big-O의 뜻 그대로
데이터의 양에따라 log 함수 꼴로 시간이 소요되는 시간복잡도이다.
우리가 log 만 쓴다면, 밑은 보통 10으로 생각되지만(상용로그),
컴퓨터는 이진수를 사용하기 때문에, 여기서의 log의 밑은 2라고 할 수 있다.
다시 주제로 돌아와서 과연 어떤 알고리즘이 O(logN)의 시간 복잡도를 가질까?
바로 '이분 탐색' 알고리즘이다.
'이분 탐색' 알고리즘은 어떤 배열에서 특정한 값을 찾는 '탐색 문제'의 알고리즘 중 하나이며, 배열의 처음부터 순차적으로 탐색하는 '선형 탐색' 과는 다르게 탐색구간을
절반씩 나누어 탐색한다.
(유일한 단점은 배열이 오름차순으로 정렬 되어있어야 한다는 점)
원리는 다음과 같다.
탐색의 시작점과 끝점이 주어지면, 해당 값의 중간 값을 탐색한다.
만약 탐색하고자 하는 값이 현재의 탐색값보다 크다면, (중간 값-1)을 끝점으로 정한다.
만약 작다면, (중간 값+1)을 시작점으로 정한다.
이것을 시작점이 초기의 끝점과 같아질 때 까지 반복한다. (중간에 값을 찾았으면 출력후 정지)
이것의 원리는 정말 신기한데, 전체의 데이터 수가 N개 라고 할 때,
한 번 탐색이 끝난 후의 데이터 수는 N/2 개 이고, 두 번째 탐색이 끝난 후의
데이터 수는 N/2x1/2개, 세번째는 N/2x1/2x1/2개.... k 번째는 (1/2)^k x N개 이다.
이때, 가장 안좋은 경우 (가장 탐색이 오래걸리는 최악의 상황) 에서 (1/2)^k x N = 1 이고,
양변에 2^k 를 곱하면, N = 2^k 가 되고, 이에 log를 씌워 주면, k = logN이 된다.
k는 탐색횟수로 이분탐색의 시간 복잡도는 O(logN) 이다.
- 다음은 원소의 개수 N 과 원소들을 입력한 뒤, 찾으려는 배열의 원소를 입력하면,
해당하는 원소의 index 를 출력해주는 알고리즘이다.
#include<stdio.h>
#include<algorithm>
using namespace std;
int a[1000001];
int main()
{
int n,ans;
int i,j,tmp;
int pos;
int start,end,middle;
scanf("%d %d",&n,&ans);
pos = -2;
start = 0;
end = n-1;
for(i=0;i<n;i++)
{
scanf("%d",&a[i]);
}
sort(a,a+n); // 배열을 오름차순으로 정렬해 주는 알고리즘
while(pos==-2 && start<=end)
{
middle = (start+end)/2;
if(a[middle]==ans){
pos = middle;
}
else if(a[middle]>ans){
end=middle-1;
}
else{
start=middle+1;
}
}
printf("%d",pos+1);
return 0;
}
이와 같이 오늘은 알고리즘에서 가장 중요한 개념 중 하나인 '시간 복잡도'에 대하여
알아보았다.
우리가 문제를 풀때, 연산이 너무 오래걸리거나,codeup, 백준과 같은
온라인 저지 사이트에 문제를 제출할 때, 만약 '시간초과' 라고 뜬다면,
이 '시간 복잡도'를 고려하지 않았을 확률이 크다.
따라서 문제를 해결하기 위해선 다양한 컴퓨팅 사고 능력을 이용하여
탐색공간을 배제하고, 수학적인 테크닉으로 코드를
더 효율적으로 작성하려는 노력이 필요하다.
