우리는 초등학교 부터 최소 고등학교 까지, 이공계를 진로로 희망하느
학생들이라면, 끊임없이 '수학'을 공부하고 또 이용합니다.
또한 자연과학, 공학, 경제학 등 여러가지 변화하는 현상을 다루고 있는 학문에
빠질 수 없이 들어가는 녀석이 있죠. 마로 '미분'과 '적분' 입니다.
우리는 어떠한 현상을 분석할때, 항상 그 데이터 자체로만 바라보지 않습니다.
조금 더 직관적이고 이해가 쉬운 '그래프'의 형태를 일반적으로 사용하여
데이터를 나타내죠. 또한 이 그래프의 변화나 미치는 영향을 분석하기 위하여
사용하는 기술이 바로 '미분' 과 '적분' 인 것이죠.
일반적으로 변화를 보기 위하여 사용하는 것이 미분,
영향을 보기 위하여 사용하는 것이 적분입니다.
(힘에 따른 에너지, 총 사용량 등등)
그러나 실생활의 문제들을 보다보면, 우리가 이용하는 이런 마법같은 기술들이
아름답게 맞아 떨어지는 경우가 거의 없습니다.
혹여나 알 수 있다고 하더라도, 그것이 꼭 아름다운 결과
다르게 표현하자면, 우리가 이해하기 쉬운 결과가 나온다는 보장도 없죠.
따라서 미분과 적분을 할 수 있는 방법은 많이 알려져 있지만, 실제 계산과 적용에선
인간의 능력이 굉장히 작게 느껴질 수 있죠.
그러나 우리에겐 방법을 떠올리지는 못하지만, 실제 계산과 적용에서
엄청나게 뛰어난 능력을 선보이는 컴퓨터가 있죠.
따라서 오늘은 이러한 미분과 적분을 컴퓨터를 통하여 나타내는
수치미분 과 수치적분 을 알아보고, 또한 이를 이용하여 실제 자연현상의
문제를 해결 할 수 있는 방법까지 알아 보도록 하겠습니다.
수치미분 과 수치적분 은 무엇일까요?
둘의 정의가 약간은 다르지만, 같은 방식으로 이해할 수 있습니다.
"함수의 미분, 적분을 컴퓨터를 이용하여 근사치로 나타내는 것" 이죠.
컴퓨터로 나타내는 것은 알겠지만, 어째서 '근사치' 일까요?
이는 앞으로의 예시를 보면 충분히 이해할 수 있는 내용이기 때문에
일단은 적용법과 예시로 넘어가 보도록 하죠!
먼저 수치미분입니다.
수치 미분을 하기 위해선 먼저 '변화율' 과 '미분계수' 를 알아야 하는데,
아래의 그림으로 보시죠.
먼저 변화율 이란, 함수 f(x)가 있을때, x 값의 변화에 따른 f(x) 값의 변화입니다.
아래 그림과 같이 두 점을 잡고, 해당 점에 대한 함수값을 알면 두점 사이의 변화로
두 점의 함수값의 변화를 나눠주면, 이것이 "점 A,P 사이의 평균 변화율"입니다.
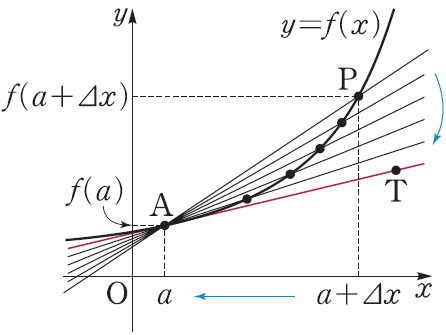
이때, 점 P가 A를 향하여 점점 다가가는 다르게 말해서 delta x 의 값이
점점 작아지는 상황을 상상해보세요.
점점 작아져서 0에 가까울 정도로 작아진다면, 이건 점 A가 갖는 순간적인 변화율이 될 것입니다. 이것을 "미분 계수" 라고 합니다.
식으로 작성하게 된다면, 다음과 같을 것입니다.

그렇다면 이것을 어떻게 컴퓨터로 계산 할 수 있을까요?
다음 식에 0을 넣으면 분모에 0이 들어가게 되니 잘못된 식이 됩니다.
그렇다면, '0에 가까운 수" 예를 들어 0.00001,0.000001 이러한 수를
h 즉, x 의 변화량으로 설정한 뒤 계산해준다면,
완전히 같다고 할 수는 없겠지만, 꽤나 "가까운" 값이 나올 것입니다.
f(x) = x^2 의 1에서의 미분값을 알아볼까요?
한 번 python 언어로 작성하여봅시다.
import numpy as np
def difference(f, x, h):
return (f(x + h) - f(x)) / h
def f(x):
return x**2
x_value = 1.0
h = 0.01
print(difference(f, x_value, h))실행해보면 2.0100000000000007 라는 값이 나옵니다.
또 h의 값을 더 작은 값으로 바꾸어 계산하면,
2에 상당히 가까운 수들이 출력됩니다.
실제로 미분 값은 2입니다.
이제 다시 생각해보니, 근사치라는 말이 조금은 와닿으실것입니다.
2가 나오기 위해선 h 가 0에 한 없이 가까워 져야 하는데,
컴퓨터를 이용하여 그러한 연산을 하는 방식은 아직까지는 개발되지 않았죠.
또는 함수의 식을 보고 여러 미분법 공식들을 이용하여 도함수를 구한 뒤,
해당 함수에 원하는 값을 넣을 수도 있겠지만, 도함수를 구하기 매우 어려운 상황이나
혹은 너무 복잡한 상황을 다룰때에는 이러한 수치 미분이 훨씬 큰 도움이 될 것입니다.
연습)
sin(x)+exp(x)+x^3 의 x = 11 에서의 도함수의 함수값을
수치미분을 이용하여 나타내어 봅시다.
import numpy as np
def difference(f, x, h):
return (f(x + h) - f(x)) / h
def f(x):
return np.sin(x)+np.exp(x)+x**3
x_value = 11.0
h = 0.001
print(difference(f, x_value, h))값: 60237.445845996255
실제 값 : 60238.123......
꽤나 유사한 값이 나왔네요.
그렇다면 이제 수치적분을 이용해볼까요?
수치적분
먼저 수치적분에서 말하는 "적분"은 정적분 입니다.
범위가 주어진 구간에서 이뤄지는 적분으로, 그래프가 주어진다면,
그래프와 x축 사이의 넓이로써 정적분을 구할 수 있습니다.
그렇다면, 그래프 아래의 넓이는 어떻게 구할까요?
여기에는 많은 방법들이 존재합니다.
그럼 한 번 상상해봅시다.
적분하고자 하는 부분을 하나의 직사각형으로 묶어볼까요?
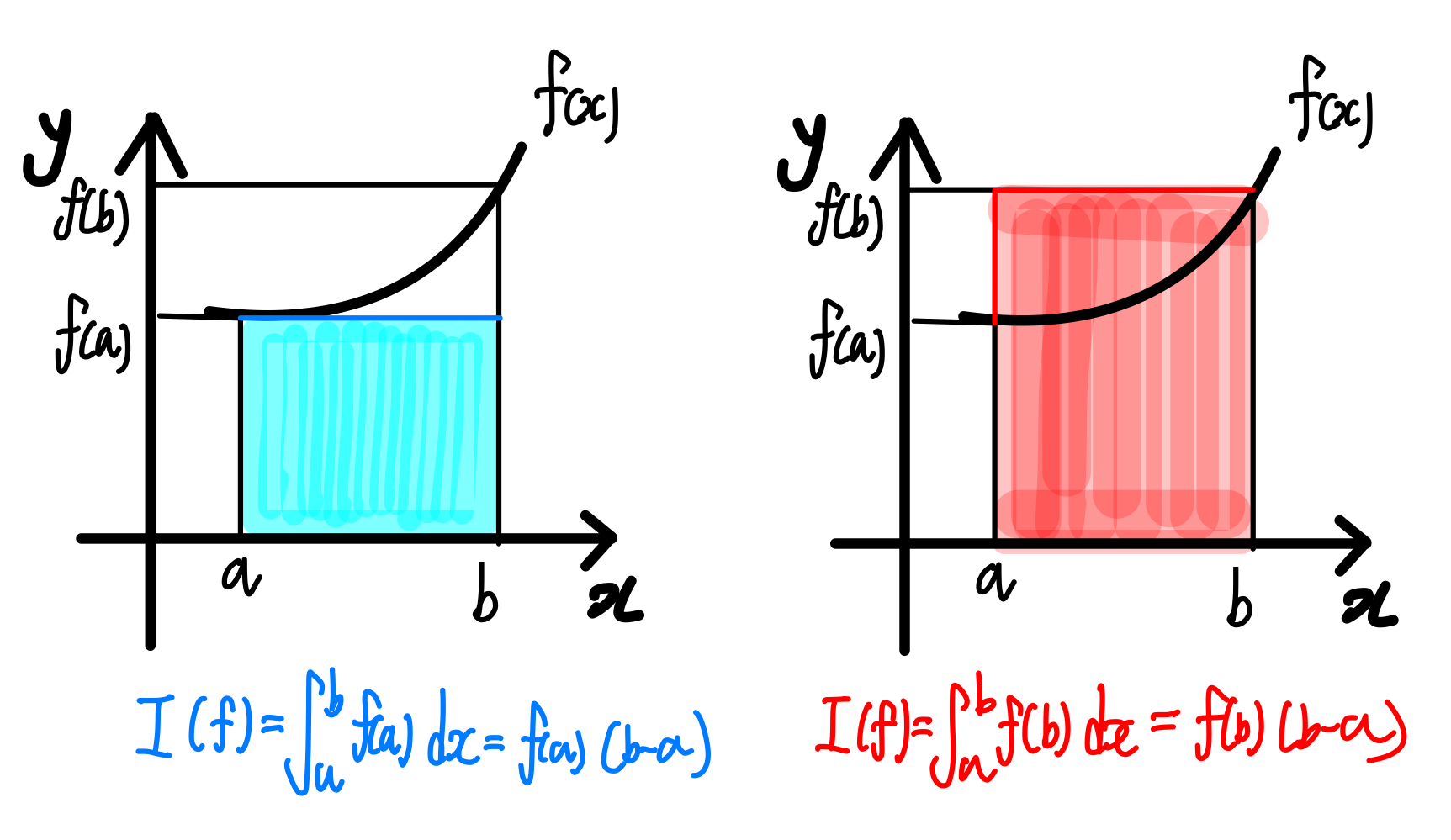
그림을 보면, 실제 그래프 아래의 넓이와 직사각형은 큰 차이가 있어보입니다.
그럼 a와 b사이를 절반으로 나누어 각각의 직사각형으로 나타낸다고 상상해봅시다.
아까보다는 조금 더 그래프 아래의 넓이와 비슷해졌지만, 아직 오차가 클 것입니다.
그럼 3등분,4등분 아주아주 큰 수로 등분해봅시다.
그렇다면 각각의 직사각형 넓이의 합은 그래프 아래의 넓이와 아주 비슷할 것입니다.
이는 정적분의 정의와 유사합니다.
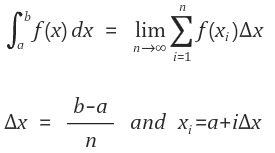
다만 여기서도 무한대 만큼으로 나누어 무한 번 더할 수는 없으므로, n을 매우 큰 수로 설정하여 그 근사치를 구할 수 있을 것입니다.
예를 들어 f(x) = x^2 의 2에서 부터 7까지의 정적분 값을 구하는 코드를 작성한다면
다음과 같습니다.
import numpy as np
def f(x):
return x**3
def riemann_sum(f, a, b, n):
x_values = np.linspace(a, b, n + 1)
y_values = f(x_values)
delta_x = x_values[1] - x_values[0]
integral_sum = np.sum(y_values * delta_x)
return integral_sum
a = 2
b = 7
n = 100000
result = riemann_sum(f, a, b, n)
print(result)값: 596.2587750267354
실제 값: 596.25
이번에도 아주 실제값과 유사하게 결과가 도출 되었습니다.
이러한 방법을 "리만 합" 이라고 합니다.
다른 방법은 평행사변형 법 인데요.
이는 곡선과 같은 그래프 아래의 굽은 부분을 평행사변형의 형태로 채워
더 효율적으로 정적분 한 값을 구할 수 있게 됩니다.
import numpy as np
def f(x):
return x**3
def vudgodtkqusgud_qjq(f, a, b, n):
x_values = np.linspace(a, b, n + 1)
y_values = f(x_values)
delta_x = x_values[1] - x_values[0]
integral_sum = np.sum((y_values[:-1] + y_values[1:]) * delta_x) / 2
return integral_sum
a = 2
b = 7
n = 100000
result = vudgodtkqusgud_qjq(f, a, b, n)
print(result)값: 596.2500000267355
아까보다 더욱 실제값에 가까운 값이 나왔네요.
그럼 이제 일상에서의 문제에 적용시켜 봅시다.
연습) (sin(x) + cos(x)) / exp(x) + log(abs(exp(x) + 3)의
0에서 부터 10 까지의 정적분 값을 평행사변형 법을 이용하여
수치적분 하여 나타내 봅시다.
import numpy as np
def f(x):
return (np.sin(x) + np.cos(x)) / (np.exp(x) + np.log(np.abs(np.exp(x) + 3)))
def vudgodtkqusgud_qjq(f, a, b, n):
x_values = np.linspace(a, b, n + 1)
y_values = f(x_values)
delta_x = x_values[1] - x_values[0]
integral_sum = np.sum((y_values[:-1] + y_values[1:]) * delta_x) / 2
return integral_sum
a = 0
b = 10
n = 100000
result = vudgodtkqusgud_qjq(f, a, b, n)
print(result)값: 0.523994819695595
실제 값: 0.523995
그렇다면 이것을 어떻게 이용할 수 있을까요?
사실 미적분이 들어가는 그 어디든 이용할 수 있습니다.
대표적인 문제를 보도록 하죠
온도가 변하지 않고, 부피가 30m^2 , 100K, 내부기체가 1mol 이 있는
계 A가 있습니다. 이러한 계의 부피가 60m^2 이 되었을때, 해당 계가 한 일의 양을 구하시오.
온도가 변하지 않는 계의 일의 양은 nRT 라는 상수에 1/ 부피 를 처음 부피에서
변한 나중의 부피만큼 정적분한 값을 곱한 값으로 정의 됩니다.
모든 값이 주어져 있으니 한 번 계산해본다면,
(리만 합으로 계산 하였음)
import numpy as np
def Work(V):
return 1/V
def riemann_sum(Work, a, b, n):
V_values = np.linspace(a, b, n + 1)
y_values = Work(V_values)
delta_V = V_values[1] - V_values[0]
integral_sum = np.sum(y_values * delta_V)
return integral_sum
a = 30
b = 60
n = 100000
result = riemann_sum(Work, a, b, n)
print(result*0.082*100)값: 5.683868380629556(J)