🌐 Introduction to Heap Sort

힙 정렬은 앞서 다루어 보았던 힙 자료구조를 이용한 정렬로 시간복잡도가 $O(nlogn)$ 인 빠른 정렬입니다. 만약 힙 자료구조가 생소하시다면 이전 포스트 를 보고 오시면 좋습니다 😄

힙 정렬은 크게 두 단계가 있습니다.

1. Build Heap
2. Sort

각각의 과정이 조금 복잡하기 때문에 두 개의 포스트로 나누어서 정리할 계획입니다. 이번 포스트는 첫번째 과정 Build Heap 에 대해 다뤄보겠습니다!

** 위에서도 말씀드렸지만 이 글은 이전 글인 Heap 에 나오는 내용들을 기반으로 작성하였습니다. 따라서 이전 글을 보시고 오시는 것을 강력 추천드립니다!

---

🌐 Build Heap

힙 정렬은 힙을 기반으로 하기 때문에 정렬해야 하는 수들로 힙을 만들어야 합니다.
이 때 어떤 힙을 만드는가는 오름차순으로 정렬할지, 내림차순으로 정렬할지에 따라 나뉩니다.

오름차순 정렬 -> Max Heap
내림차순 정렬 -> Min Heap

이렇게 하는 이유에 대해서는 두 번째 단계인 Sort에서 자연스럽게 나옵니다. 일단은 이렇게 해야한다! 라고 하고 진행해볼께요. 예시는 오름차순을 예시로 들겠습니다.

그러면 위와 같은 임의의 배열을 어떻게 힙으로 만들까요? 바로 heapify() 라는 과정을 통해 만듭니다.

⚙️ Heapify

heapify는 사실 Heap을 공부할 때 다루었었습니다. 단지 이름만 다를 뿐이죠. 바로 Bubble Down 과정이 heapify 와 거의 똑같습니다. 단지 heapify 는 특별한 조건이 하나 추가가 됩니다.
(Bubble Down 과정에 대해서 생소하시다면 역시 이전 포스트 를 참고해주세요! 😄)

🚩 조건
heapify 는 루트노드를 제외한 나머지 트리가 heap 구조를 만족할 경우에 씁니다.

⏯️ 실행
루트노드에서 Bubble Down 과정을 실행합니다.

그렇다면 heapify 를 쓴 결과는 어떻게 될까요? 루트노드를 제외하고 힙을 만족시키는 트리에서 루트노드에 Bubble down을 진행했으니 주어진 트리는 완벽한 힙구조를 갖게 될 것입니다!

그러면 heapify 가 무엇인지 알았으니 위의 임의의 배열을 한번 더 보겠습니다.

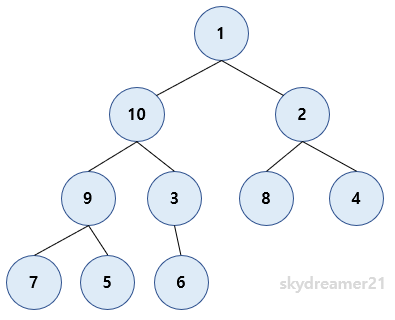
위의 트리는 주어진 배열을 트리라고 생각했을 때 시각적으로 나타낸 것입니다. 여기서 heapify를 쓸 수 있는지 생각해볼까요? 금방 답이 나옵니다. 쓸 수 없습니다. 왜냐면 아래 그림과 같이 루트노드를 제외하고 나머지 서브 트리들이 Max Heap이 아니기 때문입니다.

📝 Max Heap 복습
트리에서 부모노드는 자식노드의 값보다 항상 크거나 같은 값을 가져야 합니다.

"그럼 heapify 는 실행도 못하는 거 아니야?"

라고 생각하실 수 있지만! 트리를 좀 더 잘게 쪼개서 보면 쓸 수 있는 서브 트리들이 있습니다.

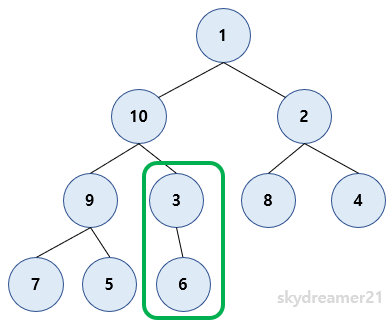
위에서 초록색 부분의 서브트리르 보면 루트노드(3) 을 제외하면 나머지는 Max Heap 입니다! 따라서 이 서브트리에서 heapify를 진행한다면 해당 서브트리는 완벽한 Max Heap 구조를 갖게 될 것입니다.

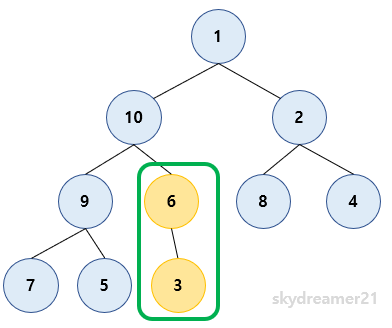
✋ 6 하나만 있는데도 Max Heap이라고 할 수 있나요?
6 원소가 하나 있다고 해도 트리라고 볼 수 있고 자식 노드가 없기 때문에 Max Heap 규칙에 위배되는 사항이 없으므로 Max Heap이라고 할 수 있습니다.

⚙️ Build Heap 과정

자, 방금 저희는 Build Heap을 위한 첫번째 heapify를 진행해 보았습니다. 그렇다면 정확히 첫번째 heapify를 진행하는 노드의 기준은 어떻게 될까요?

트리의 뒤에서 부터 확인 했을 때 처음으로 자식노드를 가지는 노드

굉장히 중요한 사실입니다! 저번 포스팅에서 Heap을 다룰 때 Heap은 완전 이진 트리를 사용한다고 했었죠? 완전 이진 트리의 특징 중 하나는 리프노드의 개수가 전체 트리 노드 개수의 절반이라는 점 입니다! 즉, 자식이 없는 노드가 전체 노드의 절반이라는 말이죠. 따라서 처음 heapify를 진행할 노드의 인덱스를 찾는다면 일일이 탐색하면서 찾는게 아닌 2로 나누는 과정을 통해 가운데에 해당하는 인덱스를 찾아주면 됩니다! 이 후 코드를 볼 때 이 점을 기억하시고 보신다면 이해가 훨씬 쉬워질 꺼에요.

그러면 나머지 흐름은 어떻게 될 지 생각해볼까요?

heapify를 쓸 수 있는 가장 작은 단위에서부터 차례대로 heapify를 써서 트리의 밑에서부터 차곡차곡 Heap 구조를 만들어 나가는 것입니다!

그러면 위의 말을 이해할 수 있도록 위의 그림 이후의 Build Heap 과정을 진행해 보도록 하겠습니다. (Max heap 구조를 가지는 트리들은 노란색으로 표현하겠습니다.)

2️⃣ 9 를 루트로 가지는 서브트리에서 heapify를 진행합니다.
- 이미 Max Heap 구조를 가지기 때문에 다음 트리로 넘어갑니다.

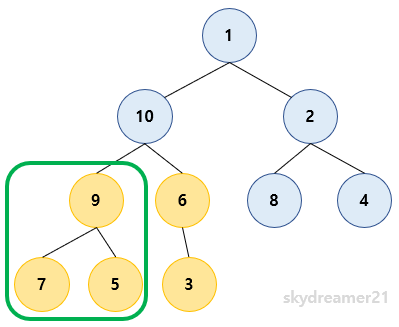
3️⃣ 2 를 루트로 가지는 서브트리에서 heapify를 진행합니다.
- 자식노드의 값이 더 크기 때문에 Bubble Down을 진행합니다.

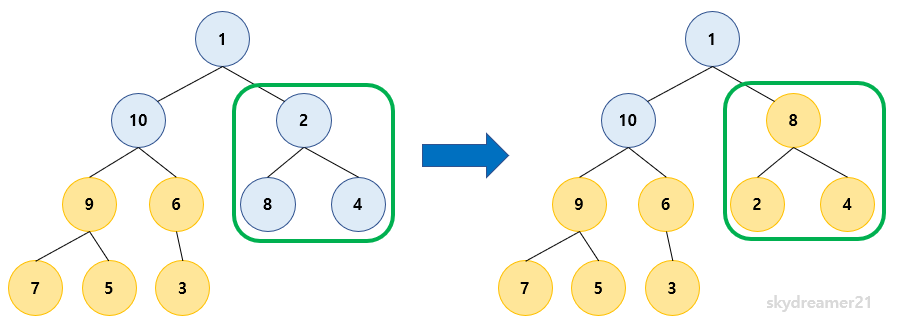
4️⃣ 10 를 루트로 가지는 서브트리에서 heapify를 진행합니다.
- 이미 Max Heap 구조를 가지기 때문에 다음 트리로 넘어갑니다.

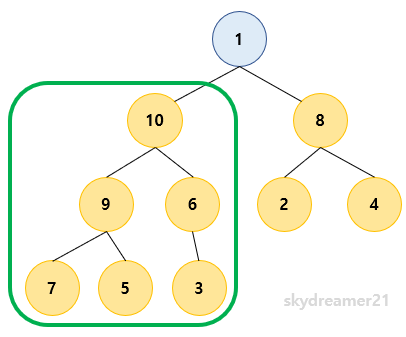
5️⃣ 전체 트리의 루트 (1) heapify를 진행합니다.
- 자식노드의 값이 더 크기 때문에 Bubble Down을 진행합니다.

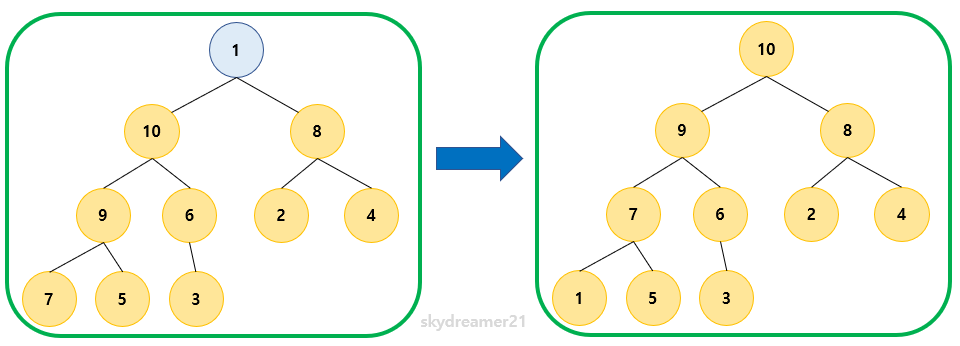
🌟 전체 트리에 대해 Heap 구조가 완성되었습니다!

⌨️ Code (java)

위의 build heap 과정을 코드로 살펴보겠습니다.

public static void buildHeap(int[] arr, boolean mode) {
    // startIdx : heapify를 시작할 첫 번째 루트 노드 인덱스
    int startIdx = ( arr.length - 1 ) / 2;

    // startIdx 부터 트리 전체 루트노드(index : 1) 까지 올라가면서 heapify를 한번씩 진행
    for (int i = startIdx; i>=1; i--) {
        maxHeapify(arr, arr.length, i);
    }
}

public static void maxHeapify(int[] arr, int size, int parent) {
    int maxIdx = size - 1;
    int leftChild = parent*2;
    // 1. 자식노드가 없다면
    if ( leftChild > maxIdx ) return;

    // 2. 디폴트로 큰 값을 가지는 자식으로 왼쪽 자식으로 설정
    int biggerChildNode = leftChild;

    // 3. 자식노드가 2개라면
    int rightChildIdx = parent*2 + 1;
    if ( rightChildIdx <= maxIdx && arr[rightChildIdx] > arr[biggerChildNode]) {
        biggerChildNode = rightChildIdx;
    }

    if (arr[biggerChildNode] > arr[parent]) {
        swap(arr, parent, biggerChildNode);
        maxHeapify(arr, size, biggerChildNode);
    }
}

사실 maxHeapify는 Heap 과정의 Bubble Down과 겹치기 때문에여기서 잘 이해하고 넘어가야 할 부분은 딱 한줄입니다.

int startIdx = ( arr.length - 1 ) / 2;
// arr.length : tree의 마지막 노드 인덱스

위의 트리 그림의 예시에서 첫번째 heapify를 진행했던 것 기억나시나요? 그 때 저희는 첫번째 heapify를 진행할 트리의 루트노드를 찾는 방법으로 2로 나누기 를 한다고 했었죠? 바로 그 과정입니다. 트리의 마지막 노드를 2로 나누었을 때 몫이 바로 처음으로 자식노드를 가지게 되는 노드의 인덱스가 됩니다!

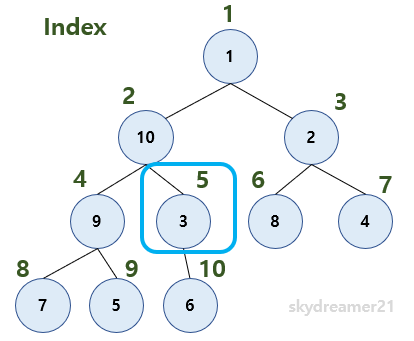
위의 그림에서 보면 마지막 노드의 인덱스 10과 처음 heapify를 진행한 노드의 인덱스 5 를 확인해보면 되겠죠?

✏️ Build Heap 의 시간 복잡도

Build Heap 의 시간 복잡도 : $O(NlogN)$

Build Heap의 시간 복잡도 계산은 간단합니다.
이전 글에서 Bubble Down 과정은 최대 연산량이 트리의 깊이와 같기 때문의 Bubble Down의 시간 복잡도는 $O(logN)$ 라고 알아보았습니다.
Build Heap에서는 Bubble Down과 같은 heapify를 전체 트리노드 개수의 절반만큼 반복을 합니다. 이를 시간 복잡도 표기법으로 나타내면 다음과 같습니다.
$O((N/2) logN) = O(NlogN)$

---

🏆 마치며...

이번 글에서 Heap Sort의 첫번째 과정인 Build Heap 에 대하여 자세히 공부해보았습니다. 다음 포스팅에서는 Heap 구조를 통해 어떻게 정렬을 진행하는지 정렬 과정에 대해 다루어보겠습니다. 🔥