🌐 What is Heap?

heap : pile of things (= 더미)

heap은 영어로 '더미'라는 뜻입니다. 무언가를 아무렇게나 쌓아둔 것을 의미합니다. 이게 어떻게 힙이라는 자료구조와 연관이 있을까요?
힙은 '더미'라는 뜻 자체 보다는 더미처럼 막 쌓아놓았을 때 돋보이는 효과에 초점을 맞추고 있습니다.

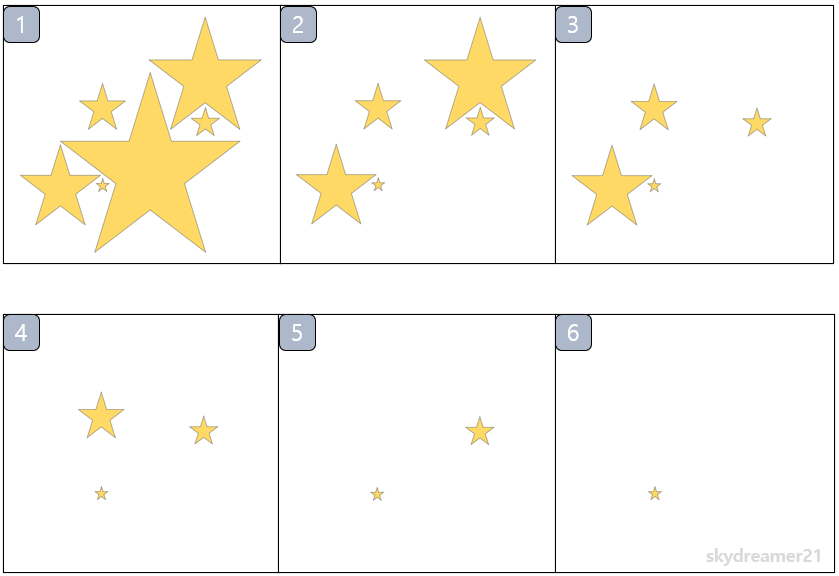
위의 그림은 별들을 가지고 힙을 시각적으로 표현해보았습니다. 1번 그림을 보시면 다양한 크기의 별들이 무작위로 배치가 되어있습니다. 이 때 우리 눈에 가장 먼저 들어오는 또는 돋보이는 가장 큰 별이 하나가 있죠? 그 별을 확인하고 지웁니다. 그러면 2번 그림이 되죠. 그러면 2번에서도 마찬가지로 눈에 띄는 가장 큰 별이 있을 것이고 확인 후 지웁니다. 이러한 과정을 별이 하나 남을 때까지 진행하죠.
그러면 이 과정에서 1번 그림에서는 가장 큰 별만 주목을 받았지만 나머지 그림들에서 모든 별들이 차례로 한번씩 주목을 받게 됩니다. 1번 그림에서 거의 눈에 띄지 않았던 가장 작았던 별도 6번 그림에서는 그 작은 별 밖에 보이질 않습니다.

힙은 이와 같은 효과를 구현한 자료구조라고 할 수 있습니다. 즉, 내가 만약 힙에서 무언가 요소를 가져왔다면 그 것은 가장 눈에 띄는 요소라는 것이 핵심입니다.

---

🌐 Heap의 종류

📘 Max Heap

• 부모노드의 값이 자식노드보다 항상 크거나 같은 Heap

📘 Min Heap

• 부모노드의 값이 자식노드보다 항상 작거나 같은 Heap

---

🌐 Heap의 구현

힙은 완전 이진 트리를 사용해서 구현하며 메서드로는 요소를 추가하는 add(), 요소를 삭제하는 delete() 가 있습니다.

📘 완전 이진 트리

완전 이진 트리는 이진 트리 중 같은 level에서 왼쪽부터 차례로 채운 트리를 이야기합니다. 한 level이 다 차기 전에는 다음 level이 존재하지 않습니다. 그렇게 때문에 완전 이진 트리에서는 원소의 개수가 주어지면 그대로 트리의 모양이 결정된다는 특징이 있죠.

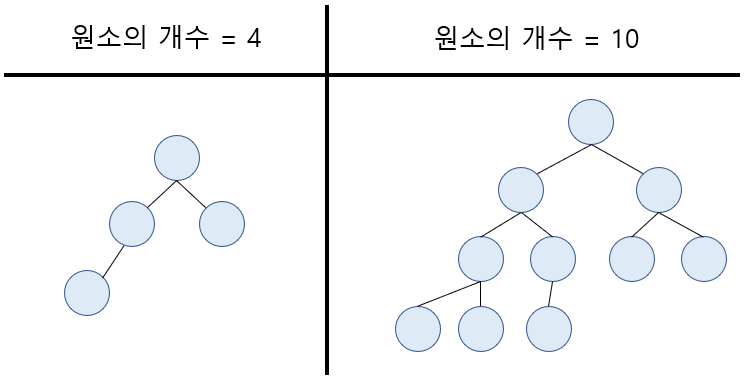
위의 그림에서 원소의 개수가 4개일 때와 10개 일때 예시를 들어보았습니다. 완전 이진 트리이기 때문에 각각의 개수에서 제가 그려놓은 트리 이외에 다른 모양의 이진 트리는 나올 수 없습니다.

✏️ parent - child 인덱싱

완전 이진 트리의 구현은 단순히 일차원 배열로 구성할 수 있습니다. 트리의 각 노드가 배열의 요소가 될 것이기 때문에 트리의 부모 자식 노드 관계를 배열에서 적절한 인덱싱으로 정해주면 될 것입니다.
인덱싱은 root 노드의 인덱스를 어떤 것으로 하냐에 따라 크게 두가지로 나눌 수 있습니다.

1. root 노드를 배열의 0번 인덱스로 지정할 경우

   • left_child = 2 * parent + 1
   • right_child = 2 * parent + 2
   • parent
     • 왼쪽 자식일 경우 (== 인덱스가 홀수)
       parent = left_child / 2
     • 오른쪽 자식일 경우 (== 인덱스가 짝수)
       parent = right_child / 2 - 1

2. root 노드를 배열의 1번 인덱스로 지정할 경우

   • left_child = 2 * parent
   • right_child = 2 * parent + 1
   • parent = child / 2

여러분이라면 어떤 방법을 쓰실 것 같나요? 2번의 경우가 인덱스를 다루기 훨씬 더 편하기 때문에 보통 root 노드의 인덱스를 1로 지정합니다.

📘 add(element)

⚙ Logic

힙에 요소를 추가하는 과정은 다음과 같습니다. (Max Heap 기준)
1. 트리의 마지막에 주어진 요소를 추가합니다.
2. 추가된 요소의 부모와 비교했을 때 부모가 작다면 자식과 부모를 swap 합니다.
3. 추가된 요소가 root 노드까지 올라가거나 부모 노드가 더 클 때까지 2번 과정을 반복합니다.

📝 Bubble up
add(element) 과정에서 위의 2 번 과정을 bubble up 이라고 합니다.

간단한 예시를 통해 과정을 살펴보겠습니다.

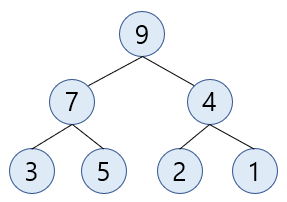
위와 같은 max heap에 8 을 추가해보겠습니다.

1. 트리의 마지막에 8을 추가합니다.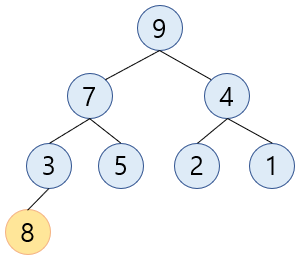

   

2. 추가된 요소의 부모(3) 과 비교했을 때 부모가 더 작기 때문에 8과 swap 합니다.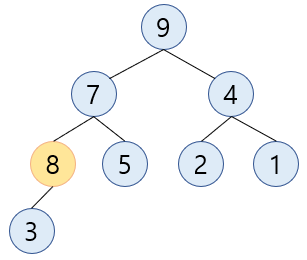

   

3. swap 된 자리에서 다시 부모 (7) 와 비교했을 때 부모가 더 작기 때문에 부모와 한번 더 swap 합니다.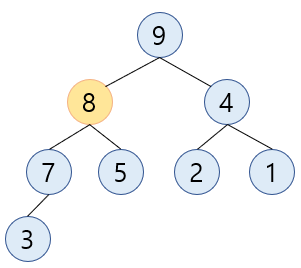

   

4. 부모(9) 와 비교 했을 때 부모가 더 크기 때문에 반복 과정을 종료합니다.

1번 과정으로 요소는 추가했지만 heap 상태가 깨졌습니다. 이를 2번 과정을 반복함으로써 추가된 요소의 자리를 찾아주고 다시 heap 상태로 만드는 흐름이라고 이해할 수 있습니다.

⌨ code (java)

위의 2번 과정에서 부모와 자식을 비교해서 swap을 하는 과정이 반복되기 때문에 재귀를 이용해 간단하게 구현해볼 수 있습니다.

public void add(int element) {
    this.heap.add(element); // heap은 java의 ArrayList 사용
    this.lastIndex++;
    bubbleUp(lastIndex);
}

private void bubbleUp (int childIdx) {
    // 추가된 요소가 root 노드까지 올라가면 종료합니다.
    if (childIdx == ROOT) return;

    int parentIdx = childIdx / 2;
    // 부모노드가 더 큰값을 가질 때까지 swap을 합니다.
    if (heap.get(childIdx) > heap.get(parentIdx)) {
        swap(parentIdx, childIdx);
        bubbleUp(parentIdx);
    }
}

📘 delete()

⚙ Logic

Heap에서 delete() 를 호출할 때 삭제되는 요소는 root 노드 입니다. 이 글의 맨 처음부분의 표현을 별 그림을 떠올려 보시면 가장 눈에 띄었던 큰 별을 없앴던 것과 같은 것입니다.
그런데 root 노드를 지우고 나면 root 노드가 없는 상태기 때문에 heap은 물론이고 트리의 형태도 갖추어지지 않습니다. 따라서 트리의 맨 마지막 요소를 root 노드로 가져옵니다. 이제 트리의 형태는 갖추어졌으니 heap만 다시 만들어주면 되겠죠? 이 과정에서는 add 와는 반대로 root노드에서 부터 자식과 비교하며 자신의 자리를 찾아 내려갑니다.

순서대로 정리를 하면 다음과 같습니다. (Max Heap 기준)

1. root 노드와 트리의 마지막 노드를 swap 합니다.
   • 이때 맨 뒤로 간 root 노드는 삭제된 노드이기 때문에 root 노드가 저장된 공간을 초기화해주고 heap의 크기를 하나 줄여줍니다.
2. root 노드의 자식 중 더 큰 값을 갖고 있는 자식을 고릅니다.
3. 2번에서 고른 자식의 값이 root 노드보다 더 크다면 해당 자식과 root 노드를 swap 합니다.
4. 자식 노드가 없거나 자식 노드의 값이 더 작거나 같을 때까지 2~3번 과정을 반복합니다.
   • 이때 2~3번 과정에서 root노드를 부모노드로 바꾸어서 적용합니다.

📝 Bubble down
delete() 과정에서 위의 2~3 번 과정을 bubble down 이라고 합니다.

add 때와 마찬가지로 예시를 하나 살펴보겠습니다. 아래의 트리에서 delete() 를 진행해볼께요.

1. root 노드(9)와 트리의 마지막 노드(1)를 swap 합니다.
   

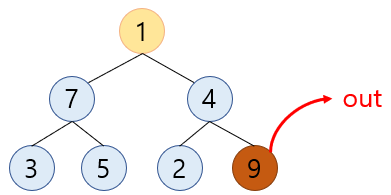
   1-1. 맨 뒤로간 root 노드를 삭제합니다. (힙의 크기 1 감소)
   

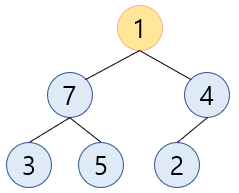
2. root 노드의 자식 중 더 큰 값을 갖고 있는 자식을 고릅니다. => 7

3. 2번에서 고른 자식의 값(7)이 root 노드(1)보다 더 크다면 해당 자식과 root 노드를 swap 합니다.
   

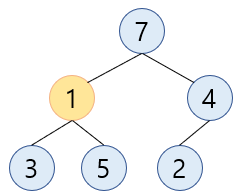
4. 새로 바뀐 위치에서 자식노드 중 큰 값(5) 과 비교했을 때 1 이 더 작기 때문에 swap을 합니다.
   

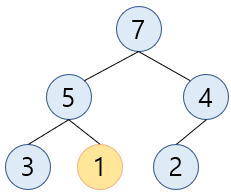
5. 1 의 자식노드가 없기 때문에 종료합니다.

⌨ code (java)

1번 과정의 swap 이후 부모와 자식을 비교하여 swap 하는 과정이 반복되기 때문에 add() 와 마찬가지로 재귀를 이용하여 구현할 수 있습니다.

public void delete() {
    if (lastIndex == 0) return;
    // 1. root와 마지막 요소 swap 합니다.
    swap(ROOT, lastIndex);
    // 1-1. tree의 마지막 요소 삭제합니다.
    heap.remove(lastIndex);
    // 1-2. 힙의 크기를 1 줄입니다.
    lastIndex--;

    // 2. 자식 노드의 값이 더 작을 때까지 bubbleDown 과정을 진행합니다.
    bubbleDown(ROOT);
}

private void bubbleDown (int parentIdx) {
    int leftChildIdx = parentIdx*2;
    // 자식 노드가 없다면 종료합니다.
    if (leftChildIdx > lastIndex) return;

    // 비교할 자식노드 값을 왼쪽 자식으로 설정합니다.
    int biggerValueChildIdx = leftChildIdx;

    int rightChildIdx = parentIdx*2 + 1;
    // 오른쪽 자식노드가 있고, 그 값이 왼쪽 자식보다 크다면 비교할 자식노드의 값을 오른쪽 자식노드로 재설정합니다.
    if (rightChildIdx <= lastIndex && heap.get(leftChildIdx) < heap.get(rightChildIdx)) {
        biggerValueChildIdx = rightChildIdx;
    }

    // 비교할 자식노드가 더 큰 값을 가진다면 부모노드와 swap 합니다.
    if (heap.get(parentIdx) < heap.get(biggerValueChildIdx)) {
        swap(parentIdx, biggerValueChildIdx);
        bubbleDown(biggerValueChildIdx);
    }
}

---

🌐 Heap의 시간 복잡도

Heap에서 요소를 추가하거나 삭제하는 데 걸리는 시간은 각각 bubbleUp 이나 bubbleDown 이 몇 번 진행되느냐에 따라 달려 있습니다. 그렇다면 가장 연산량이 많은 최악의 상황은 어떤 상황이 될까요?

• bubbleUp
  추가된 요소가 루트노드까지 올라가는 경우

• bubbleDown
  root 노드로 swap된 요소가 리프 노드까지 내려가는 경우

  📝 리프 노드
  트리에서 자식이 없는 노드를 가리킵니다.

위와 같이 끝에서 끝으로 움직이는 경우가 가장 연산량이 많겠죠! 그 때의 연산량의 주어진 트리의 깊이(depth)와 같을 것입니다. 이진 트리이기 때문에 깊이는 base를 2로 가지는 log로 표현될 수 있을 것입니다.

따라서 삽입과 삭제의 시간복잡도는 모두 $O(logN)$ 입니다.

---

🏆 마치며...

이번 포스트에서 자료구조 중 하나인 Heap에 대하여 알아보았습니다. 구현하는 과정이 간단하지 않았던 만큼 이 글을 쓰며 더욱더 확실하게 정리가 된 것 같습니다. 다음 포스팅에서는 오늘 공부한 Heap 자료구조를 활용하는 정렬인 Heap Sort에 대해서 정리해보겠습니다. ✨

오타, 잘못된 부분에 대한 지적은 언제나 환영입니다! 이해 안가는 부분 또한 피드백 또는 질문 남겨주시면 감사드리겠습니다! 🔥