
문제
바이너리 서치(LowerBound)를 사용하는 문제
-
n 나무의 수 (1 ≤ N ≤ 백만)
-
m 가져가려고 하는 나무의 길이 (1 ≤ M ≤ 20억)
-
h 설정할 수 있는 높이 (0<= h <= 10억)
-
(나무의 높이 - h) 만큼 나무를 가져갈 수 있다.
예) 나무의 높이 20, 15, 10, 17 / 절단기의 높이(h) 15
절단기 사용 후 15, 15, 10, 15 가 되어 5, 2 총(7)을 가져갈 수 있습니다. -
적어도 m 미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하세요.
- 시간 제한 1초
- 문제 링크
풀이 과정
1. 무식하게 생각하기
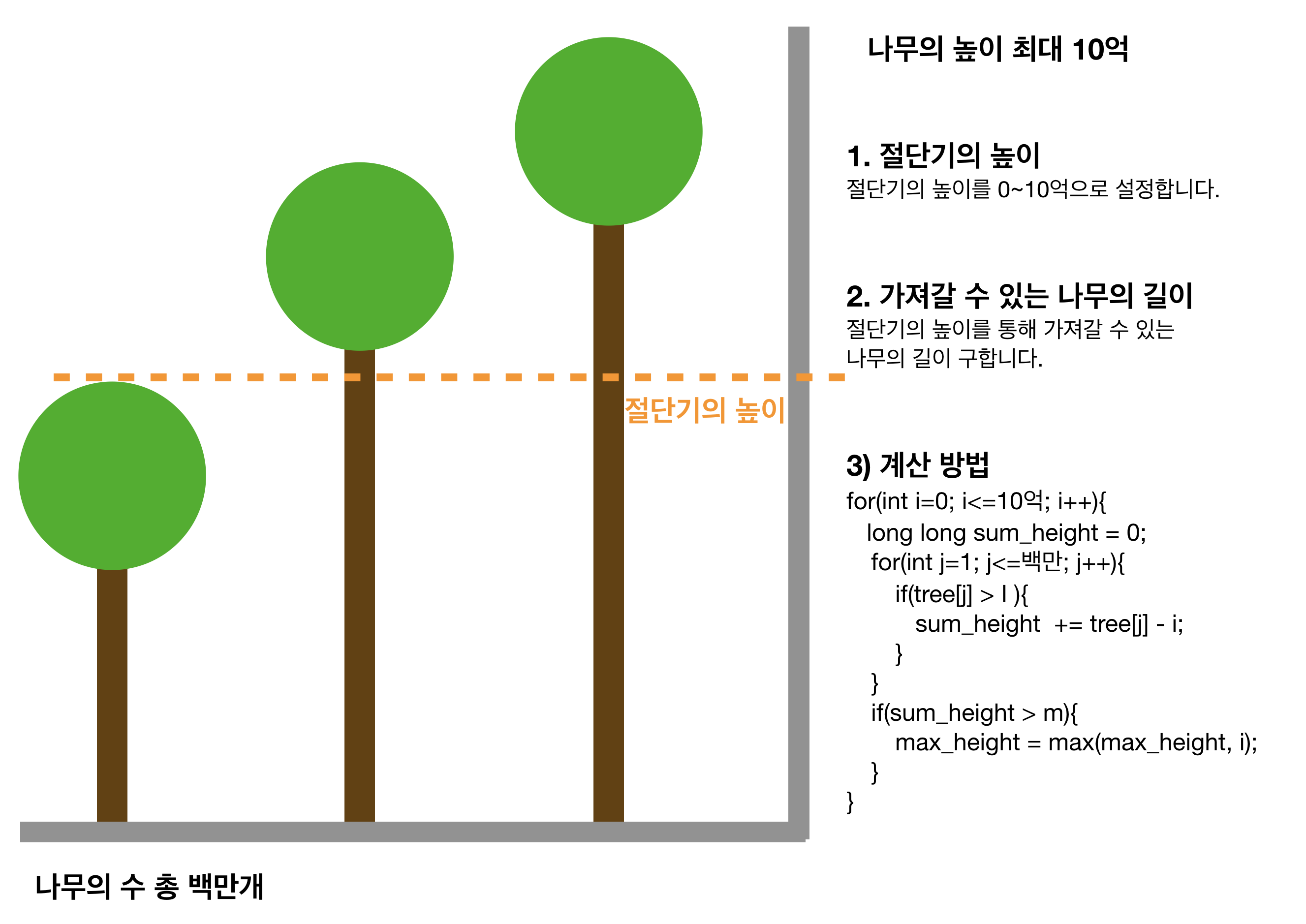
그냥 생각했을때 가장 쉬운 방법은 설정할 수 있는 높이(h)가 0~10억 이기 때문에 각 높이마다 가져갈 수 있는 나무의 길이가 적어도 m보다 같거나 큰지 계산합니다.
이때의 시간 복잡도는 O(nh) -> O(백만 * 십억) -> O(10^15) -> O(100조) -> 너무 오래 걸립니다.
2. 다른 방법이 필요해
혹시 시간이 오래 걸린다면,
1) 내가 필요없는 것을 하고 있거나,
2) 새로운 알고리즘 또는 자료구조가 필요하던가
이 문제는 2번
항상 그런것은 아닌데요, O(nh), O(n^2)인 경우 O(nlogh), O(nlogn)으로 줄이면 풀리는 경우가 있습니다.
줄이는 방법
1) 바이너리 서치(이진 탐색)
2) 정렬
3) 트리
이 문제에서는 바이너리 서치, 정렬 모두 사용할 수 있습니다.
저는 LowerBound(이진 탐색 변형) 를 사용하겠습니다.
3. 근데 LowerBound 가 뭐임?
1) LowerBound는 찾고자 하는 값 이상이 처음 나오는 위치입니다.
2) 이진 탐색의 변형으로 LowerBound가 구현되어 있습니다.
3) 중복된 값이 있는 경우에도 사용할 수 있습니다.
이진 탐색과 유사하기 때문에 먼저 이진 탐색부터 알아봅시다.
1) 이진 탐색
n=6
arr[6] = {1, 2, 4, 5, 7, 8} 일때 4의 위치를 찾으라면, 이진 탐색을 사용하면 O(logn)만에 구할 수 있습니다.
#include <stdio.h>
/*
입력받은 수의 위치(인덱스)를 정렬된 배열(arr)에서 찾는 알고리즘
시간 복잡도: O(logn)
공간 복잡도: O(n)
사용한 알고리즘: 이진 탐색
사용한 자료구조: 1차원 배열
*/
int val, result = -1, arr[6] = {1, 2, 4, 5, 7, 8};
int main(){
scanf("%d", &val);
int start = 0, end = 5, mid = -1;
while(start <= end){
mid = (start + end) / 2;
// 1) 찾고자 하는 값보다 작으면, mid 이하를 버립니다.
if(arr[mid] < val){
start = mid + 1;
}
// 2) 찾고자 하는 값보다 크면, mid 이상을 버립니다.
else if(arr[mid] > val){
end = mid - 1;
}
// 3) 찾고자 하는 값과 같으면 값을 갱신하고, 탐색을 중단합니다.
else{
result = mid;
break;
}
}
// 찾고자 하는 값이 없으면 -1을 출력합니다.
printf("%d\n", result);
}
2) LowerBound
n=6
arr[6] = {1, 2, 2, 2, 4, 4} 일때 2이상의 값이 처음으로 나오는 위치를 찾으라면?
찾으려는 값 이상이 처음으로 등장하는 위치를 구할 때는 LowerBound를 사용할 수 있습니다.
#include <stdio.h>
/*
입력받은 수 이상의 값이 정렬된 배열(arr)에서 처음으로 등장하는 위치를 찾는 알고리즘
시간 복잡도: O(logn)
공간 복잡도: O(n)
사용한 알고리즘: LowerBound(이진 탐색)
사용한 자료구조: 1차원 배열
*/
int val, result = 6, arr[6] = {1, 2, 2, 2, 4, 4};
int min(int a, int b){
return a < b ? a : b;
}
int main(){
scanf("%d", &val);
int start = 0, end = 5, mid = -1;
while(start <= end){
mid = (start + end) / 2;
// 1) 찾고자 하는 값보다 작으면, mid 이하를 버립니다.
if(arr[mid] < val){
start = mid + 1;
}
// 2) 찾고자 하는 값보다 크면, mid 이상을 버립니다.
// 찾고자 하는 값 이상이 처음으로 등장하는 위치를 찾기 때문에 가장 작은 인덱스를 갱신합니다.
else{
result = min(result, mid);
end = mid - 1;
}
}
// 찾고자 하는 값이 없으면 그 값 이상이 처음으로 등장하는 위치를 출력합니다.
printf("%d\n", result);
}4. 왜 갑자기 LowerBound?
문제에서 적어도 m을 가져갈 수 있는 높이(h)의 최대값을 구하라고 했습니다.
적어도 m은 이란 말은 m 이상의 값을 의미합니다.
높이(h)가 낮아질수록 m이 커지고
높이(h)가 커질수록 m이 작아집니다.
따라서 문제에서 찾아야하는 것은 m이상의 값이 처음으로 등장할 때의 높이(h)입니다. (이때가 문제에서 말하는 높이(h)의 최대값입니다.)
5. 시간 복잡도 계산
O(nlogh) - n 백만, logh 30 - 30 * 1000000 -> O(3천만)
시간안에 풀 수 있습니다.
코드
1. C++
#include <stdio.h>
/*
시간 복잡도: O(nlogh)
공간 복잡도: O(n)
사용한 알고리즘: LowerBound(BinarySearch)
사용한 자료구조: 1차원 배열
*/
// 나무의 최대 개수
const int kMaxCnt = 1000001;
// 나무의 최대 높이
const int kMaxHeight = 1000000000;
typedef long long lld;
int n, m, tree[kMaxCnt], result;
int max(int a, int b){
return a > b ? a : b;
}
// 현재의 높이로 가져갈 수 있는 나무 높이의 합 계산
lld GetTree(int val){
lld ret = 0;
// 나무의 높이(tree[i])가, 설정한 높이(val) 보다 커야한다.
for(int i=1; i<=n; i++){
ret += tree[i] > val ? (lld)tree[i] - val : 0;
}
return ret;
}
/*
바이너리 서치(LowerBound)
내가 찾고자 하는 값(m) 이상이 처음으로 나타나는 위치(나무의 높이, 결과)를 찾는다.
*/
void LowerBound(int start, int end){
int mid = 0;
while(start <= end){
mid = (start + end) / 2;
// 현재의 높이로 가져갈 수 있는 나무 높이의 합 계산
lld tree_result = GetTree(mid);
/*
1) 만약 가져갈 수 있는 나무 높이의 합이, 적어도 가져가야하는 값(m) 보다 작으면
높이를 낮게 설정 - 가져갈 수 있는 높이를 크게한다.
*/
if(tree_result < (lld)m){
end = mid-1;
}
/*
2) 만약 가져갈 수 있는 나무 높이의 합이, 적어도 가져가야하는 값(m) 보다 크거나 같으면
높이를 높게 설정 - 가져갈 수 있는 높이를 줄인다.
그리고 이때의 값은 적어도 M미터 이기 때문에 결과값을 갱신해준다.
*/
else{
start = mid+1;
result = max(result, mid);
}
}
}
int main(){
// 1. 입력
scanf("%d %d", &n, &m);
for(int i=1; i<=n; i++) scanf("%d", &tree[i]);
/*
2. 바이너리 서치(LowerBound)
내가 찾고자 하는 값(m) 이상이 처음으로 나타나는 위치(설정하는 높이, 결과)를 찾는다.
*/
LowerBound(0, kMaxHeight);
// 3. 출력
printf("%d\n", result);
}