문제
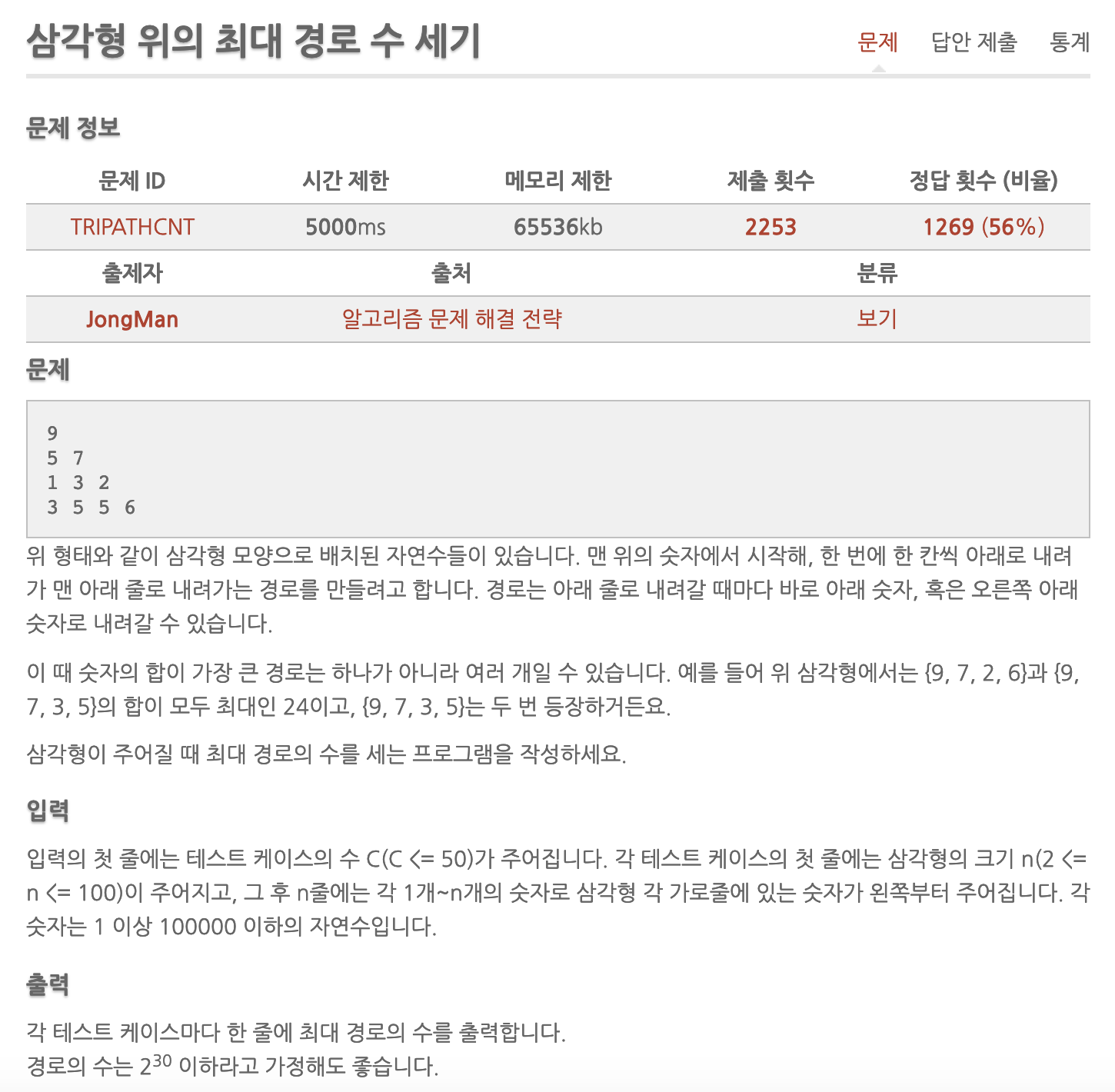
- 사진과 같은 숫자 삼각형이 있습니다.
- 맨 위의 숫자에서 시작해, 한 번에 한 칸씩 아래로 내려갑니다. 경로는 아래 줄로 내려갈 때마다 바로 아래 숫자, 혹은 오른쪽 아래 숫자로 내려갈 수 있습니다.
- 제일 아래 칸에서 얻을 수 있는 최대값의 경로 개수를 구하시오. (최대값은 여러개일 수 있습니다.)
- C(C <= 50) 테스트 케이스의 수 , n(2 <= n <= 100) 삼각형의 크기
- 시간 제한 5초
- 문제 링크
접근 과정
1. DP
- 문제를 보고 가장 먼저 떠오르는 생각은 동적 계획법 문제다. 왜냐하면, 1) 경우의 수를 구하는 문제, 2) 제일 위에서 부터 삼각형을 타고 내려왔을 때 최대값을 구하는 문제는 DP문제로 자주 접했기 때문이다. 다만, 여기서 문제는 최대값을 구하는 것이 아닌 최대값의 경로 개수를 구하는 것입니다.
2. 점화식
- d[i][j]를 i, j에서 얻을 수 있는 최대값이라고 하면, 점화식은 다음과 같이 쉽게 세울 수 있습니다.
d[i][j] = max(d[i-1][j-1], d[i-1][j]) + a[i][j];- p[i][j]를 i, j에서 최대값을 얻을 수 있는 경로의 개수라고, 하면 d[i][j]를 함께 수정해서 다음과 같이 작성 할 수 있습니다.
// 상단 오른쪽 숫자의 합이 더 크면 i-1, j-1의 정보를 받습니다.
if(d[i-1][j-1] > d[i-1][j]){
d[i][j] = d[i-1][j-1] + a[i][j];
p[i][j] = p[i-1][j-1];
// 상단 바로 위쪽 숫자의 합이 더 크면 i-1, j의 정보를 받습니다.
}else if(d[i-1][j-1] < d[i-1][j]){
d[i][j] = d[i-1][j] + a[i][j];
p[i][j] = p[i-1][j];
}
// 상단 오른쪽, 상단 바로 위쪽 숫자의 합이 같다면
// 합은 둘 중 어느것을 받아도 상관없습니다.
// 경로의 경우의 수는 두 개를 모두 받아줍니다.
else{
d[i][j] = d[i-1][j] + a[i][j];
p[i][j] = p[i-1][j-1] + p[i-1][j];
}- 그리고, i == 1, j == i일때 예외처리를 해줍니다.
3. 시간 복잡도 계산
-
1) 2중 반복문 수행시간 O(n^2) * 테스트 케이스 수: O(cn^2)
-
C(C <= 50) 테스트 케이스의 수 , n(2 <= n <= 100) 삼각형의 크기 이기 때문에 O(cn^2)은 O(5천만) 문제의 시간 제한이 5초 이기 때문에 시간이 남아돕니다.
코드
1. C++
#include <iostream>
#include <algorithm>
#define lld long long int
#define max_int 101
using namespace std;
//시간 복잡도: O(cn^2)
//공간 복잡도: O(n^2)
//사용한 알고리즘: 동적 계획법 ( Bottom-Up )
//사용한 자료구조: 2차원 배열
int t, n, result;
// a[i][j] = 삼각형에서 행 i, 열 j인 숫자
int a[max_int][max_int];
// d[i][j] = i, j에서 얻을 수 있는 가장 큰 숫자의 합
lld d[max_int][max_int];
// i, j에서 최대값을 얻을 수 있는 경로의 개수
int p[max_int][max_int];
lld max_val;
// 변수 및 배열을 초기화 하는 함수
void init() {
max_val = 0;
result = 0;
for(int i=0; i<=n; i++){
for(int j=0; j<=n; j++){
d[i][j] = 0;
p[i][j] = 0;
}
}
}
int main(){
scanf("%d", &t);
for(int test_case = 1; test_case <= t; test_case++){
scanf("%d", &n);
// 1. 변수 및 배열 초기화
init();
// 2. 숫자 삼각형의 정보를 받습니다.
for(int i=1; i<=n; i++){
for(int j=1; j<=i; j++){
scanf("%d", &a[i][j]);
}
}
// 3. 초기값 설정
d[1][1] = a[1][1];
p[1][1] = 1;
for(int i=2; i<=n; i++){
for(int j=1; j<=i; j++){
// j == 1이면 i-1, j의 정보를 그대로 받습니다.
if(j==1) {
d[i][j] = d[i-1][j] + a[i][j];
p[i][j] = 1;
}
// j == i이면 i-1, j-1의 정보를 그대로 받습니다.
else if(j==i) {
d[i][j] = d[i-1][j-1] + a[i][j];
p[i][j] = 1;
}
// 1 < j < i 일때
else {
// 상단 오른쪽 숫자의 합이 더 크면 i-1, j-1의 정보를 받습니다.
if(d[i-1][j-1] > d[i-1][j]){
d[i][j] = d[i-1][j-1] + a[i][j];
p[i][j] = p[i-1][j-1];
// 상단 바로 위쪽 숫자의 합이 더 크면 i-1, j의 정보를 받습니다.
}else if(d[i-1][j-1] < d[i-1][j]){
d[i][j] = d[i-1][j] + a[i][j];
p[i][j] = p[i-1][j];
}
// 상단 오른쪽, 상단 바로 위쪽 숫자의 합이 같다면
// 합은 둘 중 어느것을 받아도 상관없습니다.
// 경로의 경우의 수는 두 개를 모두 받아줍니다.
else{
d[i][j] = d[i-1][j] + a[i][j];
p[i][j] = p[i-1][j-1] + p[i-1][j];
}
}
// 매 행마다, 최대 값을 갱신해줍니다.
max_val = max(max_val, d[i][j]);
}
}
// 만약, d[n][j]의 정보가 최대 값이면
// 경로의 수를 결과에 더해줍니다.
for(int j=1; j<=n; j++){
if(max_val == d[n][j]){
result += p[n][j];
}
}
printf("%d\n", result);
}
}