문제
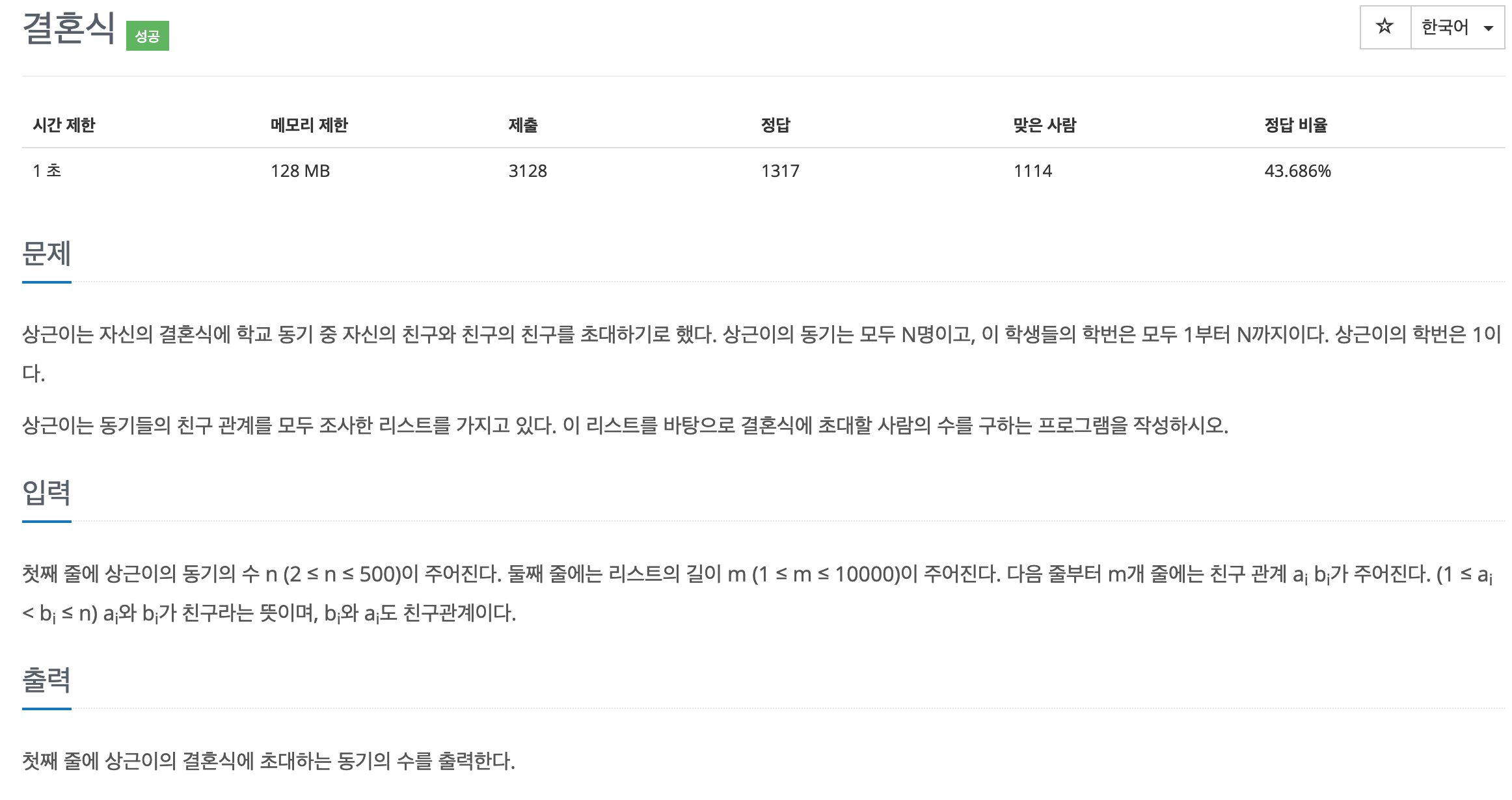
- 상근이와 친구들의 관계를 그래프로 나타내었을 때, 시작점(상근이)으로부터 최단거리가 2이하인 정점의 개수를 구하시오.
- 2 <= n <= 500 (n은 정점의 개수), 1<= m <= 10000 (m은 간선의 개수)
- 시간 제한 1초
- 문제 링크
접근 과정
1. 그래프
- 상근이와 친구들의 관계를 양방향 그래프로 설계합니다.(문제에서 a와 b가 친구 관계이면, b와 a도 친구 관계이다.) 그래프의 자료구조는 인접 리스트를 사용합니다.
- 탐색의 시간 복잡도는 인접 행렬일 때 O(n^2), 인접 리스트일 때 O(n+m)입니다. 시간 복잡도를 줄이기 위해서 인접 리스트로 구현합니다.
2. 탐색
- 상근이(시작점) 에서 부터 탐색을 시작한다. 시작점에서 부터 각 정점까지의 최단경로를 구해야합니다.
- 최단거리 알고리즘에는 대표적으로 1) 다익스트라, 2) 벨만포드, 3) 플로이드-와샬 이 있습니다만, 모든 간선의 가중치가 같을 때에는 BFS가 최단거리를 계산해줍니다. 따라서, 탐색 알고리즘으로 BFS를 사용합니다.
3. 시간 복잡도 계산
-
1) BFS의 목적은 모든 정점을 방문하는 것이고, 2) 그래프를 구현하는 자료구조 인접 리스트를 사용했습니다. 따라서 BFS를 사용하면 모든 정점과 간선을 딱 한 번씩만 방문하게 됩니다. 시간 복잡도: O(n+m)
-
2 <= n <= 500 (n은 정점의 개수), 1<= m <= 10000 (m은 간선의 개수) 이기 때문에 O(n+m)은 O(10500) 시간 안에 충분히 수행됩니다.
코드
1. C++
#include <iostream>
#include <vector>
#include <queue>
#define max_int 501
using namespace std;
//시간 복잡도: O(n+m)
//공간 복잡도: O(m)
//사용한 알고리즘: BFS
//사용한 자료구조: 인접 리스트
int n, m, a, b, result;
// 벡터를 인접 리스트로 사용합니다.
vector<int> v[max_int];
// 시작 정점으로 부터의 거리 정보를 담을 배열입니다.
int check[max_int];
void bfs(int start){
check[start] = 1;
queue<int> q;
q.push(start);
while(!q.empty()){
int node = q.front();
q.pop();
for(int i=0; i<v[node].size(); i++){
int next = v[node][i];
if(check[next] == 0){
// 다음 방문할 정점의 거리를 현재 정점까지의 거리 +1이됩니다.
check[next] = check[node] + 1;
q.push(next);
}
}
}
}
int main(){
scanf("%d %d", &n, &m);
// 1. 간선의 정보를 입력받으면서 양방향 그래프로 만들어줍니다.
for(int i=0; i<m; i++){
scanf("%d %d", &a, &b);
v[a].push_back(b);
v[b].push_back(a);
}
// 2. 시작 정점을 거리를 1로 체크하고, BFS 탐색을 시작합니다.
check[1] = 1;
bfs(1);
// 3. 시작 정점을 1로 체크했기 때문에 거리가 3이하인 정점만 개수에 더해 줍니다.
// check[i] = 0이면 방문할 수 없는 정점입니다. check[i] = 1이면 시작 정점입니다.
result = 0;
for(int i=2; i<=n; i++){
if(check[i] == 2 || check[i] == 3){
result++;
}
}
// 4. 결과 출력
printf("%d\n", result);
}2. python3
import sys, collections
input = sys.stdin.readline
print = sys.stdout.write
# 시간 복잡도: O(n+m)
# 공간 복잡도: O(m)
# 사용한 알고리즘: BFS
# 사용한 자료구조: 인접 리스트
def bfs(start):
q = collections.deque()
q.append(start)
while q:
node = q.popleft()
for next in v[node]:
if check[next] == 0:
# 다음 방문할 정점의 거리를 현재 정점까지의 거리 +1이됩니다.
check[next] = check[node] + 1
q.append(next)
n = int(input())
m = int(input())
# 간선의 정보를 저장할 인접 리스트입니다.
v = [[] for _ in range(n+1)]
# 시작 정점으로 부터의 거리 정보를 담을 리스트입니다.
check = [0] * (n+1)
# 1. 간선의 정보를 입력받으면서 양방향 그래프로 만들어줍니다.
for _ in range(m):
a, b = map(int, input().split())
v[a].append(b)
v[b].append(a)
# 2. 시작 정점을 거리를 1로 체크하고, BFS 탐색을 시작합니다.
check[1] = 1
bfs(1)
# 3. 시작 정점을 1로 체크했기 때문에 거리가 3이하인 정점만 개수에 더해 줍니다.
# check[i] = 0이면 방문할 수 없는 정점입니다. check[i] = 1이면 시작 정점입니다.
result = 0
for i in range(2, n+1):
if check[i] == 2 or check[i] == 3:
result += 1
# 4. 결과 출력
print("%d\n" % result)3. java(openJDK)
import java.util.*;
// 시간 복잡도: O(n+m)
// 공간 복잡도: O(m)
// 사용한 알고리즘: BFS
// 사용한 자료구조: 인접 리스트
public class Main {
static int n, m, a, b, result;
static ArrayList<Integer>[] v = new ArrayList[501];
static int[] check;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
for(int i=1; i<=n; i++){
v[i] = new ArrayList<>();
}
for(int i=0; i<m; i++){
a = sc.nextInt();
b = sc.nextInt();
v[a].add(b);
v[b].add(a);
}
check = new int[n+1];
check[1] = 1;
bfs(1);
result = 0;
for(int i=2; i<=n; i++){
if(check[i] == 2 || check[i] == 3){
result++;
}
}
System.out.println(result);
}
public static void bfs(int start){
Queue<Integer> q = new LinkedList<>();
q.offer(start);
while(!q.isEmpty()){
int node = q.poll();
for(int next:v[node]){
if(check[next] == 0){
check[next] = check[node] + 1;
q.offer(next);
}
}
}
}
}