문제

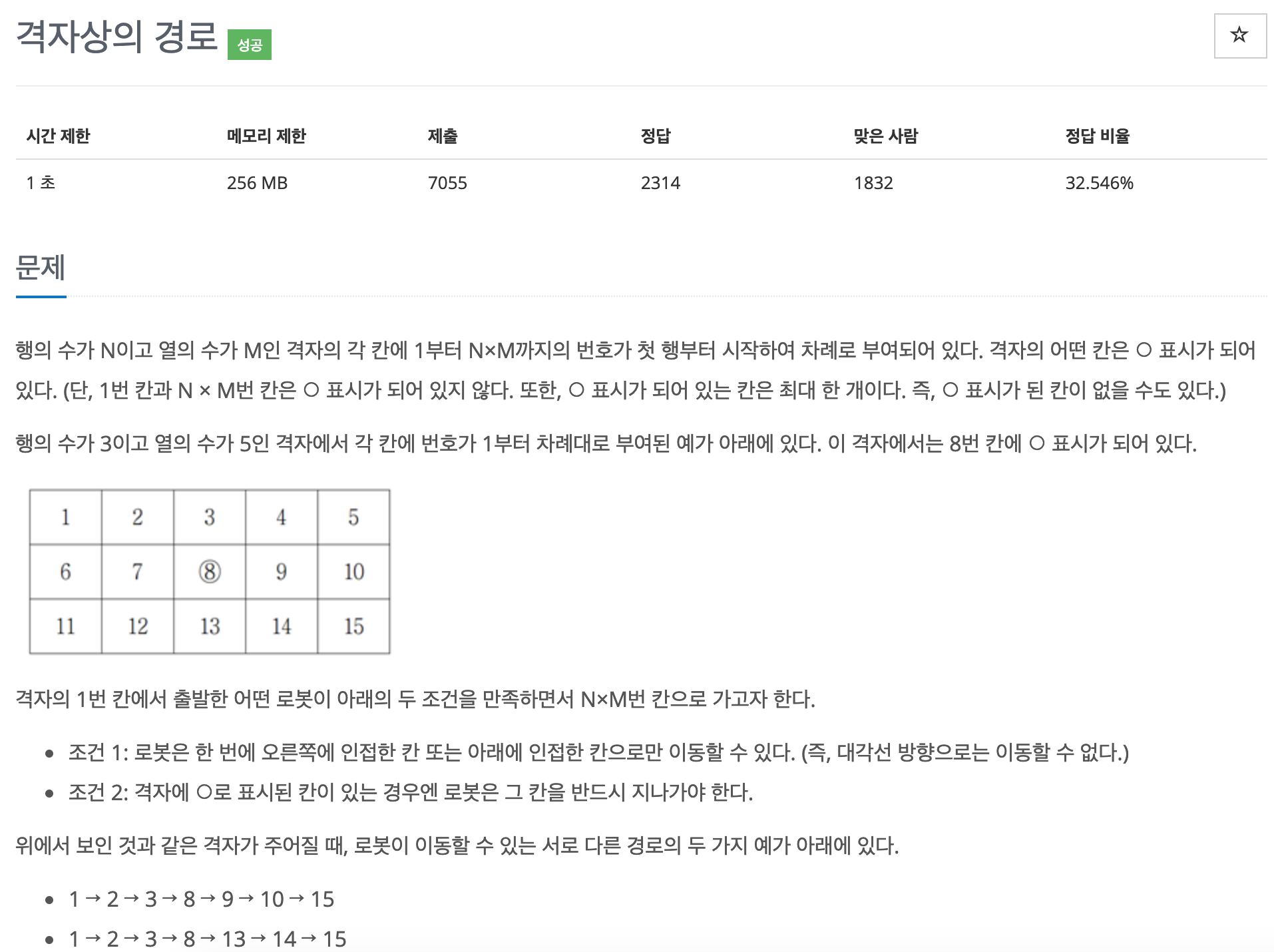
• 행의 수가 n, 열의 수가 m인 격자칸에 1부터 n*m까지 차례로 번호가 부여됩니다.
• 1) 오른쪽으로 한 칸 또는 2) 아래쪽으로 한 칸 이동할 수 있습니다.
• k 번째 칸은 꼭 통과해야 합니다. (k가 0이면 꼭 통과해야 하는 칸은 없습니다.)
• 조건을 만족하면서 (1, 1) 칸에서 시작해서 (n, m) 칸까지 이동할 수 있는 경우의 수를 구하시오.
• n(1 <= n <= 15) 행의 수, m(1 <= m <= 15) 열의 수, 칸의 번호를 나타내는 정수 k(k=0 또는 1 < K < N×M)
• 시간 제한 1초
• 문제 링크

---

접근 과정

1. 쉽게 쉽게

• 정보 올림피아드 문제이지만, 쉽게 풀려면 쉽게 풀립니다.
  점화식은 다음과 같습니다.

// d[i][j]는 i, j로 올 수 있는 경우의 수
// i, j로 올 수 있는 경우의 수는 위 칸으로 올 수 있는 경우의 수 + 왼쪽 칸으로 올 수 있는 경우의 수
d[i][j] = d[i-1][j] + d[i][j-1];

조금 신경 쓰이는 부분은 1) k번째 칸의 행, 열 값, 2) k가 0일때 처리 입니다.

2. k번째 칸 계산

• 음..k를 m으로 나눴을때 몫을 행, 나머지를 열.. 근데 나머지가 0일때는...생각하지말구
  그냥 2중 for문으로 첫번째 칸부터 마지막 칸까지 번호를 채웁니다. n,m 의 제한이 15로 너무 작습니다.

3. k가 0일 때

• 꼭 통과해야하는 칸이 없으면...어떻게 하지
  그냥 상위에서 분기처리 합니다.

    if(k!=0) {
      // 점화식 수행
    }
    else{
      // 점화식 수행
    }

4. 시간 복잡도 계산

• 1) O(nm) = 이중 for문

• n(1 <= n <= 15) 행의 수, m(1 <= m <= 15) 열의 수 이기 때문에 O(mn^2)은 O(15 * 15) = O(225) 문제의 시간 제한이 1초 이기 때문에 시간이 남아돕니다.

코드

1. C++

#include <iostream>
#include <cstring>
#define max_int 16

using namespace std;

//시간 복잡도: O(n^2)
//공간 복잡도: O(n^2)
//사용한 알고리즘: 동적 계획법(Bottom-up)
//사용한 자료구조: 2차원 배열

int n, m, k;
int a[max_int][max_int];
// d[i][j]는 i, j로 올 수 있는 경우의 수
int d[max_int][max_int];

int main(){
    scanf("%d %d %d", &n, &m, &k);

    // 분기 처리
    if(k!=0) {
        // 꼭 통과해야하는 칸의 i, j
        int mid_i, mid_j;

        // 1번째 칸부터 n*m 칸 까기 차례로 채웁니다.
        int count = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                count++;
                // 현재 칸이 k번째 칸이면 mid_i, mid_j를 갱신해줍니다.
                if (count == k) {
                    mid_i = i;
                    mid_j = j;
                }
            }
        }

        // (1, 1)에서 k번째 칸 까지 점화식 수행
        d[1][1] = 1;
        for (int i = 1; i <= mid_i; i++) {
            for (int j = 1; j <= mid_j; j++) {
                if (i == 1 && j == 1) continue;
                d[i][j] = d[i - 1][j] + d[i][j - 1];
            }
        }

        int mid_result = d[mid_i][mid_j];

        // 초기화
        memset(d, 0, sizeof(d));

        // k번째 칸에서 n*m 번째 칸까지 점화식 수행
        d[mid_i][mid_j] = 1;
        for (int i = mid_i; i <= n; i++) {
            for (int j = mid_j; j <= m; j++) {
                if (i == mid_i && j == mid_j) continue;

                d[i][j] = d[i - 1][j] + d[i][j - 1];
            }
        }
        // 결과 출력
        printf("%d\n", mid_result * d[n][m]);
    }
    else{
        
        // 첫번째 칸에서 n*m 번째 칸까지 점화식 수행
        d[1][1] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (i == 1 && j == 1) continue;
                d[i][j] = d[i - 1][j] + d[i][j - 1];
            }
        }
        printf("%d\n", d[n][m]);
    }
}