백준 14500 테트로미노

skyepodium·2020년 5월 1일
CDFSJava백준 14500백준 테트로미노백트래킹알고리즘자바테트로미노
6

sw 역량 테스트

목록 보기
10/12
post-thumbnail

인생 뭐 될 때까지 하는 거지

문제

DFS를 사용해서 합의 최댓값을 구하는 문제. (ㅜ 모양은 예외처리 합니다)

  1. n 종이의 크기 (4 ≤ N, M ≤ 500)

  2. 종이 한칸의 수는 (1<= aij <= 1,000)

  3. 5개의 모양을 종이에 놓아서 합의 최대값을 구합니다.
    (모양은 회전, 대칭이 가능합니다.)

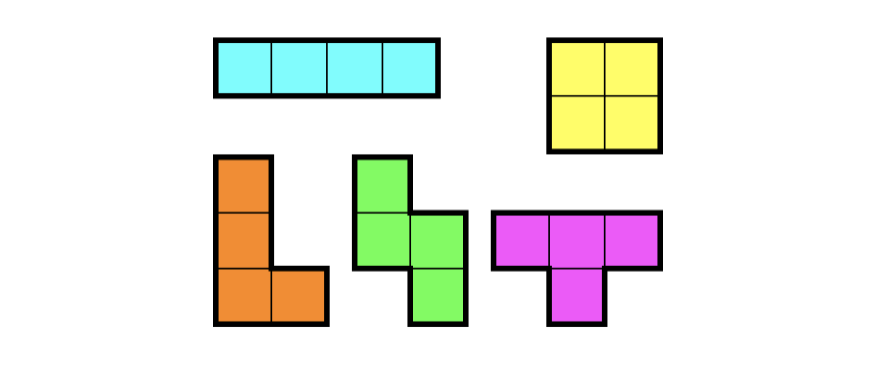
1. 첫인상

귀찮아

각각의 모양을 만들고, 대칭, 회전할 생각에 귀찮아 집니다.

그런데 잘 생각 해보면 (사실, 생각은 잘 안나고 누가 말해주면, 그런가 같더라구요)

ㅜ를 제외한 나머지 4개의 모양은 길이가 4인 DFS의 탐색 모양입니다.

아래 그림과 같이 가운데 시작 점으로 부터 파란색으로 색칠된 영역을 탐색합니다.

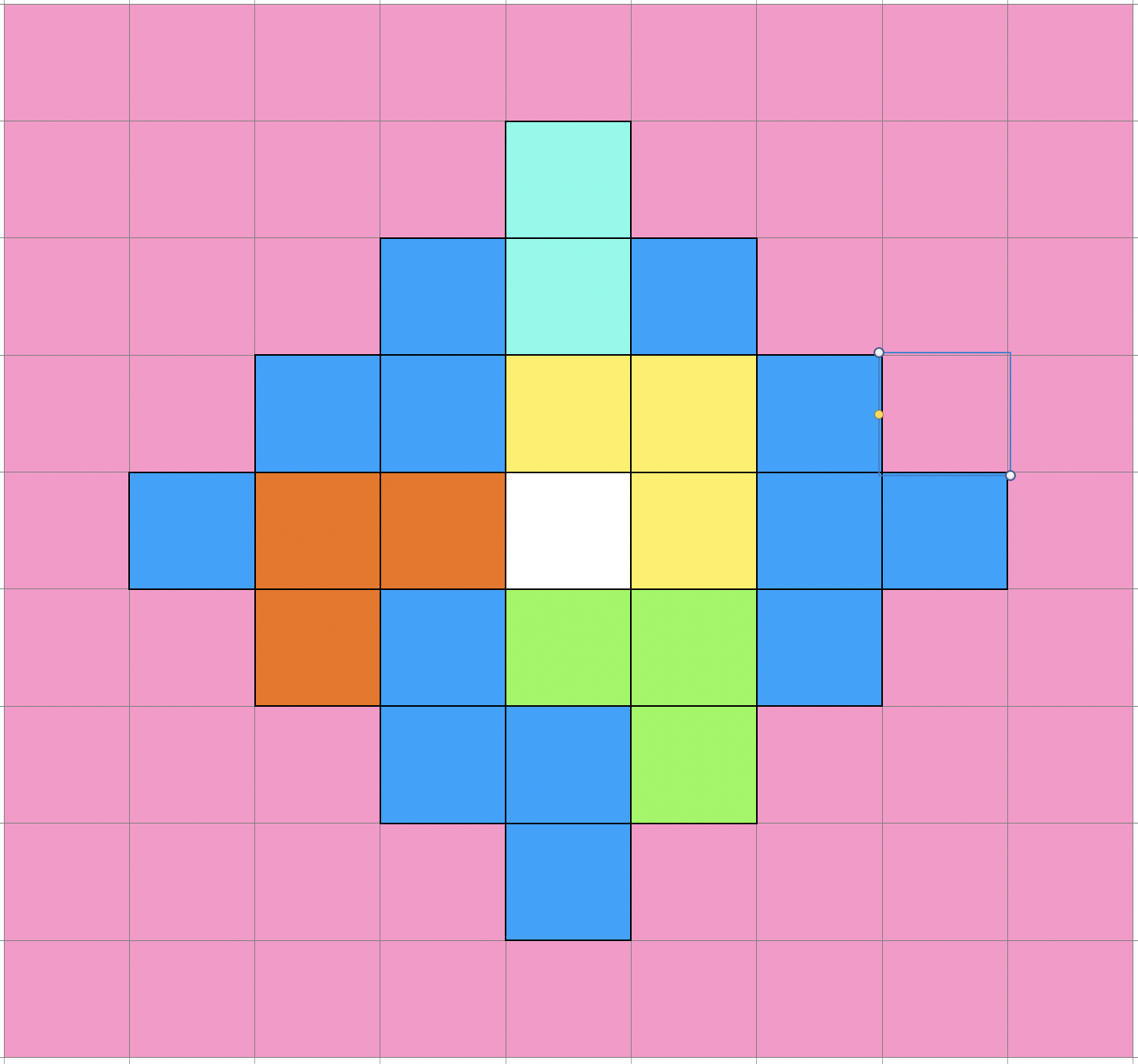
다만 ㅜ 모양은 최대 길이가 3인 DFS입니다. 그렇기 때문에 따로 만들어 주어야합니다.

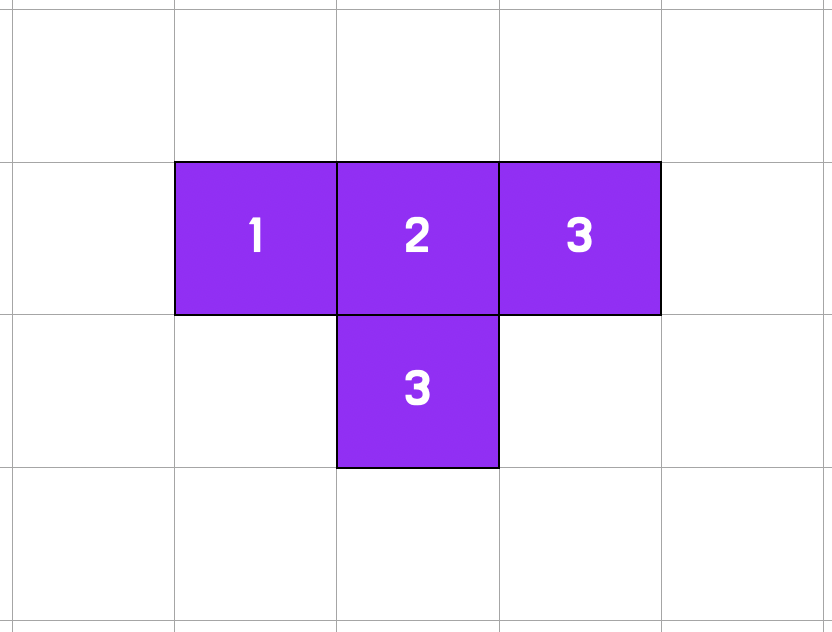
2. 접근 과정

문제를 작게 나눠보면 다음과 같습니다.
1. 입력

  1. 각각의 모양 검사
  • ㅜ 를 제외한 4개 DFS 사용
  • ㅜ 를 검사하는 함수
  1. 출력

1, 3번은 일반적인 입력과 출력이기 때문에 2번의 모양 검사를 중심적으로 보겠습니다.

3. ㅜ 를 제외한 4개 DFS 사용

1) 평소의 DFS랑 다르다.

평소에 사용하는 깊이 우선 탐색은 방문한 점을 다시 방문하지 않습니다.

하지만, 모양을 대칭, 회전 시키기 위해서는 한점을 다시 방문해야합니다.

이렇게 모든 경우의 수를 전부 고려하는 알고리즘을 백트래킹 이라고 합니다.

방문한 점을 다시 방문하기 위해서 탐색을 완료하면 그 정점을 방문하기 전 상태로 되돌려 놓아야합니다.

2) BFS는 안돼나요?

BFS는 돌아올 수 없습니다.

재귀는 내부적으로 스택을 사용하기 때문에 거꾸로 되돌아가는게 가능합니다.

하지만, BFS는 되돌아갈 수 없습니다.

3) DFS 어떻게 되돌아오나요?

for(int i=0; i<4; i++){
    int nx = x + dx[i];
    int ny = y + dy[i];

    // 지도 넘어가는 경우 검사
    if(nx < 1 || nx > n || ny < 1 || ny > m) continue;

    // 방문하지 않은 점이면
    if(!check[nx][ny]) {

        // 들어가기전 체크해주고
        check[nx][ny] = true;

        dfs(nx, ny, sum_value + a[nx][ny], length + 1);
        // 하나의 탐색을 완료하면 여기로 돌아옵니다.

        // 나올때 체크를 해제합니다.
        check[nx][ny] = false;
    }
}

4. ㅜ 를 검사하는 함수

1) 방법

4개의 모양의 왼쪽 상단을 기준 (0, 0) 으로 삼고 검사합니다.

2) 예시

void check_exshape(int x, int y){

    int sum_value = 0;
    // 1. ㅜ
    if(x>=1 && x+1<=n && y>=1 && y+2<=m){
        sum_value = a[x][y] + a[x][y+1] + a[x][y+2] + a[x+1][y+1];
        result = max(result, sum_value);
    }

    // 2. ㅏ
    if(x >= 1 && x+2 <=n && y>=1 && y+1<=m){
        sum_value = a[x][y] + a[x+1][y] + a[x+2][y] + a[x+1][y+1];
        result = max(result, sum_value);
    }

    // 3. ㅗ
    if(x-1 >= 1&& x <=n && y >=1 && y+2 <=m){
        sum_value = a[x][y] + a[x][y+1] + a[x][y+2] + a[x-1][y+1];
        result = max(result, sum_value);
    }

    // 4. ㅓ
    if(x-1 >= 1 && x+1 <=n && y >=1 && y+1 <=m){
        sum_value = a[x][y] + a[x][y+1] + a[x-1][y+1] + a[x+1][y+1];
        result = max(result, sum_value);
    }
}

5. 시간 복잡도 계산

각점에 대해 DFS 수행
각점 = O(n^2)
DFS = O(36) 왜냐하면, 첫점에서 갈 수 있는 경우 4, 2번째 점 3, 3번째 점 3 = 4 3 3 = 36

따라서 전체 시간복잡도는 36 * O(n^2) = O(n^2) 상수 제거,

n이 500이기 때문에 n^2은 2500, 1억이 1초이기 때문에

시간안에 충분히 풀 수 있습니다.

6. 코드

1) c++

#include <iostream>
#define max_int 501
using namespace  std;

/*
    시간 복잡도: O(n^2)
    공간 복잡도: O(n^2)
    사용한 알고리즘: 백트래킹 (DFS)
    사용한 자료구조: 2차원 배열
 */

// a는 지도 정보를 저장할 2차원 배열
int n, m, a[max_int][max_int], result;
bool check[max_int][max_int];

// dx, dy는 인접한 4방향을 나타내는 방향벡터
// 0, 1, 2, 3 순서대로 왼쪽, 오른쪽, 아래쪽, 위쪽
int dx[] = {0, 0, 1, -1};
int dy[] = {-1, 1, 0, 0};


/*
    ex, ey는 ㅜ 모양의 4가지 회전 방향일때 정보를 저장합니다.
    만약 각각 분리했으면 바로 아래 주석 부분과 같습니다. (ㅜ, ㅏ, ㅗ, ㅓ)
 */
int ex[4][4] = {{0, 0, 0, 1}, {0, 1, 2, 1}, {0, 0, 0, -1}, {0, -1, 0, 1}};
int ey[4][4] = {{0, 1, 2, 1}, {0, 0, 0, 1}, {0, 1, 2, 1}, {0, 1, 1, 1}};

/*
    // ㅜ
    int ex_1_x[] = {0, 0, 0, 1}, ex_1_y[] = {0, 1, 2, 1};

    // ㅏ
    int ex_2_x[] = {0, 1, 2, 1}, ex_2_y[] = {0, 0, 0, 1};

    // ㅗ
    int ex_3_x[] = {0, 0, 0, -1}, ex_3_y[] = {0, 1, 2, 1};

    // ㅓ
    int ex_4_x[] = {0, -1, 0, 1}, ex_4_y[] = {0, 1, 1, 1};
 */


int max(int a, int b){
    return a > b ? a : b;
}

// DFS 로 4가지 모양 검사 (ㅜ 제외)
void dfs(int x, int y, int sum_value, int length){
    // 길이가 4 이상이면 종료햅줍니다.
    if(length >= 4){
        result = max(result, sum_value);
        return;
    }

    for(int i=0; i<4; i++){
        int nx = x + dx[i];
        int ny = y + dy[i];

        // 지도 넘어가는 경우 검사
        if(nx < 1 || nx > n || ny < 1 || ny > m) continue;

        // 방문하지 않은 점이면
        if(!check[nx][ny]) {

            // 들어가기전 체크해주고
            check[nx][ny] = true;

            dfs(nx, ny, sum_value + a[nx][ny], length + 1);

            // 나올때 체크를 해제합니다.
            check[nx][ny] = false;
        }
    }
}


// ㅜ 모양 검사
void check_exshape(int x, int y){

    for(int i=0; i<4; i++){

        bool isOut = false;
        int sum_value = 0;

        for(int j=0; j<4; j++){
            int nx = x + ex[i][j];
            int ny = y + ey[i][j];

            if(nx < 1 || nx > n || ny < 1 || ny > m) {
                isOut = true;
                break;
            }
            else {
                sum_value += a[nx][ny];
            }
        }
        if(!isOut) {
            result = max(result, sum_value);
        }
    }
    // 만약 배열로 정보 저장 안해놓았으면 아래처럼 작성할 수 있습니다.

//    int sum_value = 0;
//    // 1. ㅜ
//    if(x>=1 && x+1<=n && y>=1 && y+2<=m){
//        sum_value = a[x][y] + a[x][y+1] + a[x][y+2] + a[x+1][y+1];
//        result = max(result, sum_value);
//    }
//
//    // 2. ㅏ
//    if(x >= 1 && x+2 <=n && y>=1 && y+1<=m){
//        sum_value = a[x][y] + a[x+1][y] + a[x+2][y] + a[x+1][y+1];
//        result = max(result, sum_value);
//    }
//
//    // 3. ㅗ
//    if(x-1 >= 1&& x <=n && y >=1 && y+2 <=m){
//        sum_value = a[x][y] + a[x][y+1] + a[x][y+2] + a[x-1][y+1];
//        result = max(result, sum_value);
//    }
//
//    // 4. ㅓ
//    if(x-1 >= 1 && x+1 <=n && y >=1 && y+1 <=m){
//        sum_value = a[x][y] + a[x][y+1] + a[x-1][y+1] + a[x+1][y+1];
//        result = max(result, sum_value);
//    }
}


int main(){

    // 1. 입력
    scanf("%d %d", &n, &m);

    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            scanf("%d", &a[i][j]);
        }
    }


    // 2. 2차원 배열 각각의 원소에서 검사를 수행합니다.
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            // 1) DFS 로 검사

            // 방문했던 점을 또 방문해야하기 때문에
            // 들어가기전 체크를 해주고, 끝났을때 체크를 해제해줍니다.
            check[i][j] = true;
            dfs(i, j, a[i][j], 1);

            // 체크를 해제하면 무한루프에 들어가 않을까 걱정할 수 있습니다.
            // 길이로 재귀를 중단시키기 때문에, 수행횟수는 4 * 3 * 3, 한점에서 최대 36번 수행됩니다.
            check[i][j] = false;

            // 2) ㅏ 모양 검사
            check_exshape(i, j);
        }
    }


    // 3. 출력
    printf("%d\n", result);
}

2) java

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

/*
    시간 복잡도: O(n^2)
    공간 복잡도: O(n^2)
    사용한 알고리즘: 백트래킹 (DFS)
    사용한 자료구조: 2차원 배열
 */

public class Main {

    private static int n, m, a[][], result;
    private static Boolean check[][];
    private static int dx[] = {0, 0, 1, -1};
    private static int dy[] = {-1, 1, 0, 0};

    private static int ex[][] = {{0, 0, 0, 1}, {0, 1, 2, 1}, {0, 0, 0, -1}, {0, -1, 0, 1}};
    private static int ey[][] = {{0, 1, 2, 1}, {0, 0, 0, 1}, {0, 1, 2, 1}, {0, 1, 1, 1}};
    public static void main(String[] args) throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        // 1. 입력
        st = new StringTokenizer(br.readLine());
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());

        a = new int[n+1][m+1];
        check = new Boolean[n+1][m+1];
        for(int i=1; i<=n; i++){
            for(int j=1; j<=m; j++){
                check[i][j] = false;
            }
        }

        for(int i=1; i<=n; i++){
            st = new StringTokenizer(br.readLine());
            for(int j=1; j<=m; j++){
                a[i][j] = Integer.parseInt(st.nextToken());
            }
        }
        // 2. 계산
        // 2. 2차원 배열 각각의 원소에서 검사를 수행합니다.
        for(int i=1; i<=n; i++){
            for(int j=1; j<=m; j++){
                // 1) DFS 로 검사

                // 방문했던 점을 또 방문해야하기 때문에
                // 들어가기전 체크를 해주고, 끝났을때 체크를 해제해줍니다.
                check[i][j] = true;

                dfs(i, j, a[i][j], 1);

                // 체크를 해제하면 무한루프에 들어가 않을까 걱정할 수 있습니다.
                // 길이로 재귀를 중단시키기 때문에, 수행횟수는 4 * 3 * 3, 한점에서 최대 36번 수행됩니다.
                check[i][j] = false;

                // 2) ㅏ 모양 검사
                check_exshape(i, j);
            }
        }

        // 3. 출력
        System.out.println(result);
    }

    public static int max(int a, int b){
        return a > b ? a: b;
    }

    // DFS 로 4가지 모양 검사 (ㅜ 제외)
    public static void dfs(int x, int y, int sum_value, int length){
        // 길이가 4 이상이면 종료햅줍니다.
        if(length >= 4){
            result = max(result, sum_value);
            return;
        }

        for(int i=0; i<4; i++){
            int nx = x + dx[i];
            int ny = y + dy[i];

            // 지도 넘어가는 경우 검사
            if(nx < 1 || nx > n || ny < 1 || ny > m) continue;

            // 방문하지 않은 점이면
            if(check[nx][ny] == false) {

                // 들어가기전 체크해주고
                check[nx][ny] = true;

                dfs(nx, ny, sum_value + a[nx][ny], length + 1);
                // 하나의 탐색을 완료하면 여기로 돌아옵니다.

                // 나올때 체크를 해제합니다.
                check[nx][ny] = false;
            }
        }
    }

    // ㅜ 모양 검사
    public static void check_exshape(int x, int y){

        for(int i=0; i<4; i++){

            Boolean isOut = false;
            int sum_value = 0;

            for(int j=0; j<4; j++){
                int nx = x + ex[i][j];
                int ny = y + ey[i][j];

                if(nx < 1 || nx > n || ny < 1 || ny > m) {
                    isOut = true;
                    break;
                }
                else {
                    sum_value += a[nx][ny];
                }
            }
            if(!isOut) {
                result = max(result, sum_value);
            }
        }
        // 만약 배열로 정보 저장 안해놓았으면 아래처럼 작성할 수 있습니다.

//    int sum_value = 0;
//    // 1. ㅜ
//    if(x>=1 && x+1<=n && y>=1 && y+2<=m){
//        sum_value = a[x][y] + a[x][y+1] + a[x][y+2] + a[x+1][y+1];
//        result = max(result, sum_value);
//    }
//
//    // 2. ㅏ
//    if(x >= 1 && x+2 <=n && y>=1 && y+1<=m){
//        sum_value = a[x][y] + a[x+1][y] + a[x+2][y] + a[x+1][y+1];
//        result = max(result, sum_value);
//    }
//
//    // 3. ㅗ
//    if(x-1 >= 1&& x <=n && y >=1 && y+2 <=m){
//        sum_value = a[x][y] + a[x][y+1] + a[x][y+2] + a[x-1][y+1];
//        result = max(result, sum_value);
//    }
//
//    // 4. ㅓ
//    if(x-1 >= 1 && x+1 <=n && y >=1 && y+1 <=m){
//        sum_value = a[x][y] + a[x][y+1] + a[x-1][y+1] + a[x+1][y+1];
//        result = max(result, sum_value);
//    }
    }
}
profile
skyepodium
callmeskye
이전 포스트

백준 13458 시험 감독

다음 포스트

백준 19238 스타트 택시

5개의 댓글

comment-user-thumbnail
최우석
2020년 9월 12일

잘 보고 갑니다~

1개의 답글
comment-user-thumbnail
정수인
2022년 1월 12일

글 잘 보았습니다.
5번 오타 있습니다. 시간 복잡도 계산에서 n^2은 250000입니다.

답글 달기
comment-user-thumbnail
이상협
2022년 10월 15일

생각은 잘 안나고 누가 말해주면 그런거 같다는 말 너무 공감되네요 ㅋㅋㅋ ㅠㅠ 잘 배우고갑니다..

답글 달기
comment-user-thumbnail
박상준
2022년 10월 17일

문제가 너무 더러워요..

답글 달기