입사문제에 퇴사라는 이름이 아이러니
2019.11.10 수정
O(n)으로 풀 수 있어요ㅠㅠ
예전에는 O(n^2)으로 작성했어요. 곧 고치겠습니다.
문제
n일 동안 일을 해서 n+1일에 받을 수 있는 최대금액을 계산하는 문제
-
n 일을 할 수 있는 기간 (1 <= n <= 15)
-
t[i]는 i번째 일을 완료하는데 걸리는 기간 (1 ≤ Ti ≤ 5)
-
p[i]는 i번째 일을 완료하고 받을 수 있는 금액 (1 ≤ Pi ≤ 1,000)
-
예시

1일에 일을 하면 T1(3)일동안 일을 합니다. 1일 포함 2일 3일을 일을 하고 4일에 다시 일을 할 수 있습니다.
- 시간 제한 2초
- 문제 링크
풀이 과정
1. 접근 과정
1) DP 그리고, 문제의 조건 다시 확인하기
딱 봐도 동적 계획법(DP)의 향이 느껴집니다.
여러가지 방법으로 풀 수 있지만, 첫느낌 그대로 DP로 가봅시다.
점화식 다 떠나서, 극단적인 예를 볼께요
1) N (일할 수 있는 기간)이 5
2) T (i 번째 일을 완료하는데 걸리는 시간)
3) P (i 번째 일을 완료하고 받을 수 있는 금액)
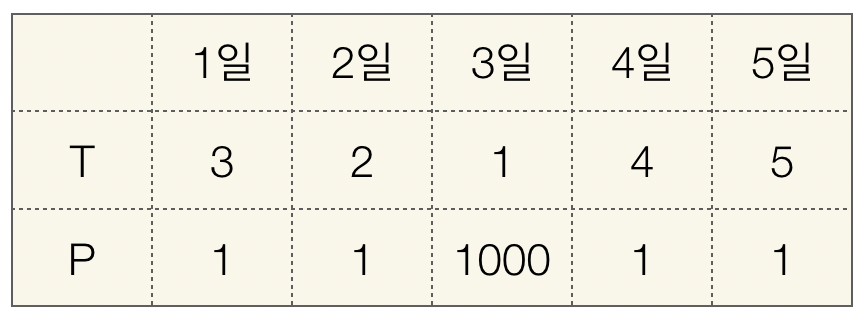
이라고 하면 N+1 일인 5일째에 받을 수 있는 최대 금액은 얼마인가요?
1000 입니다. 1, 2, 4일에 일을 안하고 3일 딱 하루만 일을 하면됩니다.
문제에는 적혀있지 않지만, i 번째 날에 일을 안할 수도 있습니다.
2) 돈 언제 받지?

문제의 예시에서 3일에 기간 1인 일을 하면 돈은 언제 받을까요? 3일 ? 4일?
정하기 나름인데, 저는 하루 건너 4일에 받는 것으로 정했습니다.
1) 따라서, i번째 날 일을하면 i + t[j]날 돈을 받습니다.
n번째 날 기간 1인 일을 하면 n+1일날 돈을 받습니다.
2) 따라서, n+1번째 날까지 검사해줍니다.
3) 점화식 세우기
d[i]를 i번째 날에 받을 수 있는 최대 금액이라고 정의해봅시다.

다시 문제의 예시에서 4일에 돈을 받는 경우는 어떤게 있나요?
1) 1일에 일을 시작하고, 4일에 1을 받음
2) 1일에 일을 안하고, 2일에 일을 시작해서 1을 받음
3) 1, 2일에 일을 안하고 3일에 일해서 1000을 받음
4) 1, 2, 3, 4일에 일을 안하고 0을 받음
1), 2), 3), 4) 중 최대값이 d[4] 가 됩니다.
점화식을 세워보면 다음과 같이 작성할 수 있습니다.
// i번째 날 일을하면 i + t[j]날 돈을 받기 때문에,
// n+1번째 날까지 진행해줍니다.
for(int i=1; i<=n + 1; i++){
for(int j=1; j<i; j++){
// 1) j 번째 날에서 일을 안하고 i 번째 날까지 온 경우(j < i)
d[i] = max(d[i], d[j]);
// 2) j 번째 날에서 t[j] 기간 동안 일을하고 보상을 p[j] 받은 경우
// 그 보상은 j + t[j] 날 받습니다.
if(j + t[j] == i){
d[i] = max(d[i], d[j] + p[j]);
}
}
}3. 시간 복잡도 계산
0) n 제한은 15
1) 2중 for문 O(n^2) 이기 때문에 O(255)
2) 시간안에 충분히 풀고 시간이 남아돕니다.
코드
0. C++ O(n) - 2019.11.10 추가
왜 내가 예전에 O(n^2)으로 작성했을까ㅠㅠㅠㅠ
#include <stdio.h>
/*
시간 복잡도: O(n)
공간 복잡도: O(n)
사용한 알고리즘: 동적 계획법(bottom-up, tabulation)
사용한 자료구조: 1차원 배열
*/
const int kMaxCnt = 17;
/*
d[i]는 i번째 날에 받을 수 있는 최대 금액
1) i번째 날에 일을 했을 경우
d[i+t[i]] = max(d[i+t[i]], d[i] + p[i]);
2) i번째 날에 일을 하지 않았을 경우
d[i+1] = max(d[i+1], d[i]);
*/
int n, t[kMaxCnt], p[kMaxCnt], d[kMaxCnt], result;
int max(int a, int b){
return a > b ? a : b;
}
int main(){
//1. 문제 입력
scanf("%d", &n);
for(int i=1; i<=n; i++){
scanf("%d %d", &t[i], &p[i]);
}
// 2. DP 수행
for(int i=1; i<=n; i++){
// 1) i번째 날에 일을 했을 경우
if(i+t[i] <=n+1){
d[i+t[i]] = max(d[i+t[i]], d[i] + p[i]);
// 최대값 갱신
result = max(result, d[i+t[i]]);
}
// 2) i번째 날에 일을 하지 않았을 경우
d[i+1] = max(d[i+1], d[i]);
// 최대값 갱신
result = max(result, d[i+1]);
}
// 3. 출력
printf("%d\n", result);
}1. C++
#include <iostream>
#define max_int 16
using namespace std;
/*
시간 복잡도: O(n^2)
공간 복잡도: O(n)
사용한 알고리즘: 동적 계획법(bottom-up, tabulation)
사용한 자료구조: 배열
*/
/*
t는 일을 완료하는데 걸리는 기간
p는 일을 완료하고 받을 수 있는 금액
d[n]은 n+1에 받을 수 있는 최대 금액을 의미합니다.
아래의 예시에서 1일에 일을 하면 3일동안 일을 하기 때문에 4일에 금액을 받습니다.
1 2 3 4
t 3 5 1 1
p 10 20 10 20
d 0 0 0 10
*/
int n, t[max_int], p[max_int], d[max_int], result;
// 두수 a, b에서 최대값을 구하는 함수 (삼항 연산자 사용)
int max(int a, int b){
return a > b ? a : b;
}
int main(){
// 1. 입력
scanf("%d", &n);
for(int i=1; i<=n; i++){
scanf("%d %d", &t[i], &p[i]);
}
// 2. DP (bottom-up) 수행
// i번째 날 일을하면 i + t[j]날 돈을 받기 때문에,
// n+1번째 날까지 진행해줍니다.
for(int i=1; i<=n + 1; i++){
for(int j=1; j<i; j++){
// 1) j 번째 날에서 일을 안하고 i 번째 날까지 온 경우(j < i)
d[i] = max(d[i], d[j]);
// 2) j 번째 날에서 t[j] 기간 동안 일을하고 보상을 p[j] 받은 경우
// 그 보상은 j + t[j] 날 받습니다.
if(j + t[j] == i){
d[i] = max(d[i], d[j] + p[j]);
}
}
// 3) 최대값을 갱신해줍니다.
result = max(result, d[i]);
}
// 3. 출력
printf("%d\n", result);
}
2. java
import java.io.*;
/*
시간 복잡도: O(n^2)
공간 복잡도: O(n)
사용한 알고리즘: 동적 계획법(bottom-up, tabulation)
사용한 자료구조: 배열
*/
public class Main{
/*
t는 일을 완료하는데 걸리는 기간
p는 일을 완료하고 받을 수 있는 금액
d[n]은 n+1에 받을 수 있는 최대 금액을 의미합니다.
아래의 예시에서 1일에 일을 하면 3일동안 일을 하기 때문에 4일에 금액을 받습니다.
1 2 3 4
t 3 5 1 1
p 10 20 10 20
d 0 0 0 10
*/
public static int [] t, p, d;
public static int n, result;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 1. 입력
n = Integer.parseInt(br.readLine());
// n + 1일 까지 계산합니다.
t = new int[n + 2];
p = new int[n + 2];
d = new int[n + 2];
for(int i=1; i<=n; i++){
String[] s = br.readLine().split(" ");
t[i] = Integer.parseInt(s[0]);
p[i] = Integer.parseInt(s[1]);
}
// 2. DP (bottom-up) 수행
// i번째 날 일을하면 i + t[j]날 돈을 받기 때문에,
// n+1번째 날까지 진행해줍니다.
for(int i=1; i<=n + 1; i++){
for(int j=1; j<i; j++){
// 1) j 번째 날에서 일을 안하고 i 번째 날까지 온 경우(j < i)
d[i] = max(d[i], d[j]);
// 2) j 번째 날에서 t[j] 기간 동안 일을하고 보상을 p[j] 받은 경우
// 그 보상은 j + t[j] 날 받습니다.
if(j + t[j] == i){
d[i] = max(d[i], d[j] + p[j]);
}
}
// 3) 최대값을 갱신해줍니다.
result = max(result, d[i]);
}
// 3. 출력
System.out.println(result);
}
// 두수 a, b에서 최대값을 구하는 함수 (삼항 연산자 사용)
public static int max(int a, int b){
return a > b ? a : b;
}
}3. python3
'''
시간 복잡도: O(n^2)
공간 복잡도: O(n)
사용한 알고리즘: 동적 계획법(bottom-up, tabulation)
사용한 자료구조: 배열
'''
'''
t는 일을 완료하는데 걸리는 기간
p는 일을 완료하고 받을 수 있는 금액
d[n]은 n+1에 받을 수 있는 최대 금액을 의미합니다.
아래의 예시에서 1일에 일을 하면 3일동안 일을 하기 때문에 4일에 금액을 받습니다.
1 2 3 4
t 3 5 1 1
p 10 20 10 20
d 0 0 0 10
'''
# 1. 입력
n = int(input())
t = [0]
p = [0]
# n + 1일 까지 계산합니다.
d = [0] * (n+2)
result = 0
for i in range(n):
a, b = map(int, input().split())
t.append(a)
p.append(b)
# 2. DP (bottom-up) 수행
for i in range(1, n+2):
for j in range(1, i):
# 1) j 번째 날에서 일을 안하고 i 번째 날까지 온 경우(j < i)
d[i] = max(d[i], d[j])
# 2) j 번째 날에서 t[j] 기간 동안 일을하고 보상을 p[j] 받은 경우
# 그 보상은 j + t[j] 날 받습니다.
if j + t[j] == i:
d[i] = max(d[i], d[j] + p[j])
# 3) 최대값을 갱신해줍니다.
result = max(result, d[i])
# 3. 출력
print(result)4개의 댓글
문제를 풀면서 생각을 해봤는데, python 기준으로 조금 더 직관적인 코드는 이런 형태가 되지 않을까 싶어요.
max_profit = [0]
for i in range(len(appointments) + 1):
for j in range(0, i):
if (j + appointments[j]['duration'] == i):
max_profit[i] = max(max_profit[i], max_profit[j] + appointments[j]['price'])
max_profit.append(max(max_profit))매번 이전의 것들 중 길이가 맞는 것과 최대를 구하는 것보다는, 그 다음 값에다가 여태까지의 최대를 집어넣고 max operation을 돌리면 어떨까해요.



좋은 풀이 감사드립니다.
개인적으로 이미 if문이 들어간다면
if j + t[j] == i:
d[i] = max(d[i], d[j] + p[j])
else:
d[i] = max(d[i], d[j])
가 조금 더 낫지 않을까 싶습니다. 필요없는 연산이 한번 줄어드니까요. if연산은 이미 한 상태고