문제

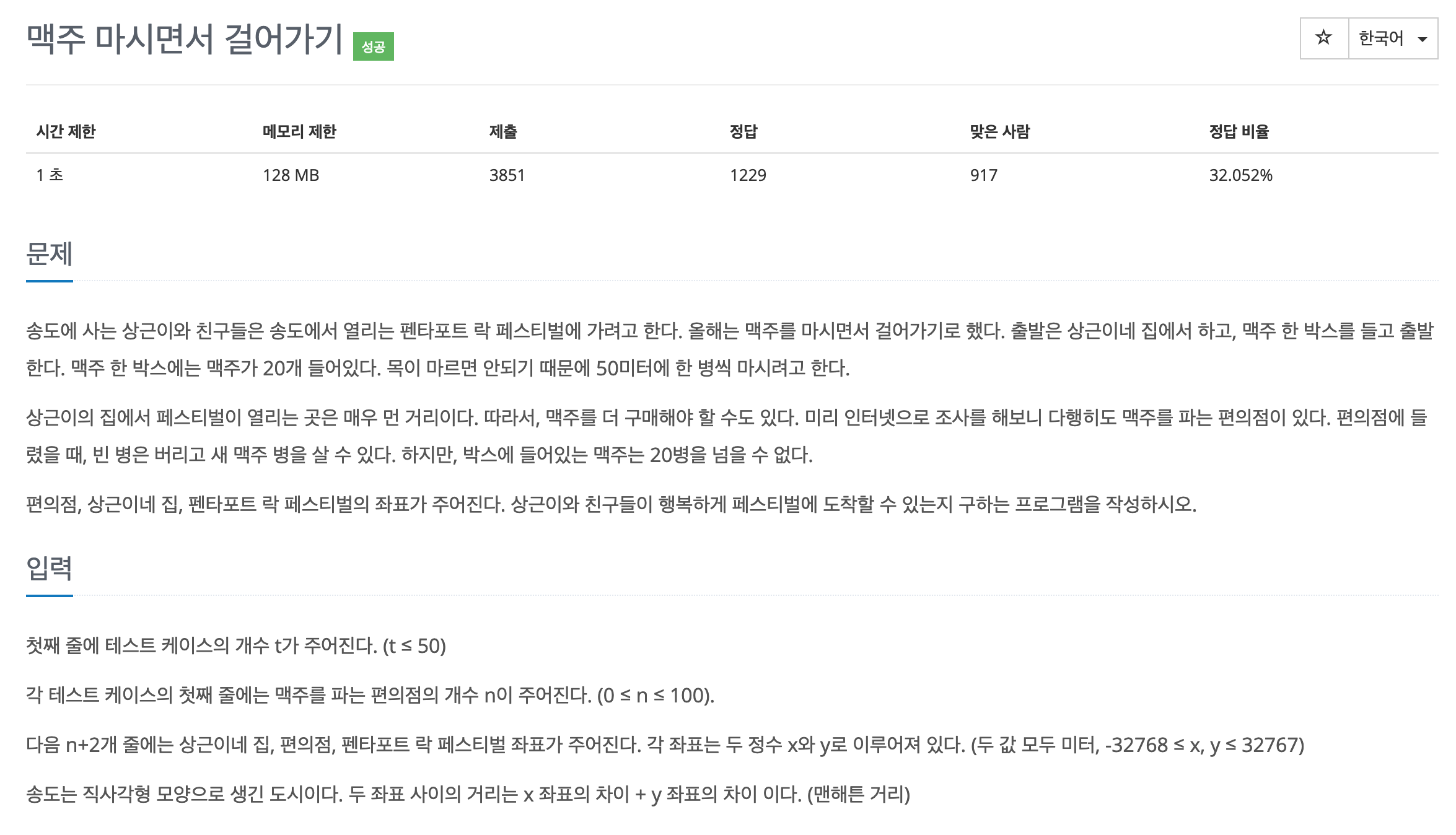
• 집 1개, 페스티벌 1개, 편의점 n개 -> 총 n+2개의 정점이 주어집니다.
• 각 정점의 x, y 좌표가 주어집니다.
• 두 정점 사이의 거리는 'x 좌표의 차이 + y 좌표의 차이' 이다. (맨해튼 거리)
• 50미터 마다 맥주 한병씩을 마시고, 한 박스에 20개가 들어있고, 편의점에서 한 박스를 모두 교체할 수 있습니다.
• 출발할 때 맥주 한박스를 들고 출발합니다.
• 집에서 출발해서 페스티벌에 도착할 때 까지 맥주가 떨어지지 않으면 happy, 떨어진다면 sad를 출력하세요.
• n(1 <= n <= 100) 편의점의 수
• 시간 제한 1초
• 문제 링크

---

접근 과정

1. 그래프

• 이 문제는 간선을 만들고, 시작 정점에서 탐색하는 문제입니다.
  보통 그래프 문제는 1) 정점들의 정보, 2) 간선들의 정보를 모두 제공합니다만, 이 문제에서는 간선의 정보가 주어지지 않기 때문에 간선을 직접 만들어야 합니다.

2. 간선

• 주어진 맨해튼 거리 계산법을 사용해서 1) 두 정점 사이의 거리가 1000미터 이하면 간선을 만들고, 2) 1000미터 초과면 간선을 만들지 않습니다.

3. 탐색

• 그래프 탐색 기법중 BFS, DFS...아무거나 사용해도 상관 없습니다. 마지막 정점에 도착할 수 있는지 여부만 검사합니다.

4. 시간 복잡도 계산

• 1) O(n^2) -> 1) 간선을 만들기 위해 2중 for문 사용 O(n^2) + 2) DFS 의 시간 복잡도는 O(V+E) 이 문제에서 간선의 수는 n^2 - O(n^2) -> 상수생략 O(n^2)

• n(1 <= n <= 100) 이기 때문에 O(n)은 O(100) 문제의 시간 제한이 1초 이기 때문에 시간안에 풀 수 있습니다.

코드

1. C++

#include <iostream>
#include <vector>

#define max_int 102
using namespace std;

//시간 복잡도: O(n^2)
//공간 복잡도: O(n^2)
//사용한 알고리즘: DFS(완전 탐색, 탐색 알고리즘 아무거나 사용해도 상관없음)
//사용한 자료구조: 인접 리스트

int t, n;
struct info{
    int x;
    int y;
};

// 간선의 정보를 저장하는 인접 리스트
vector<int> v[max_int];
// 정점 방문 여부를 저장할 배열
bool check[max_int];

// 완전 탐색
void dfs(int node){
    check[node] = true;
    for(int i=0; i<v[node].size(); i++){
        int next = v[node][i];
        if(check[next] == false){
            dfs(next);
        }
    }
}

// 맨해튼 거리 계산 함수
int cal_dist(int x1, int y1, int x2, int y2){
    int dist = abs(max(x1, x2) - min(x1, x2)) + abs(max(y1, y2) - min(y1, y2));

    return dist <= 1000 ? true : false;
}

// 변수 초기화 함수
void init(){
    for(int i=0; i<n+2; i++){
        check[i] = false;
        v[i].clear();
    }
}

int main(){
    scanf("%d", &t);

    for(int test_case=1; test_case<=t; test_case++){

        scanf("%d", &n);

        // 1. 초기화
        init();

        // 2. 정점의 x좌표, y좌표를 벡터에 입력받습니다.
        vector<info> node(n+2);
        for(int i=0; i<n+2; i++){
            scanf("%d %d", &node[i].x, &node[i].y);
        }

        // 3. 이중 for문으로 모든 간선을 검사해서
        // 1) 두 정점 사이를 이동할 수 있으면 간선을 만들고,
        // 2) 이동 할 수 없으면 간선을 만들지 않습니다.
        for(int i=0; i<n+2; i++){
            for(int j=i+1; j<n+2; j++){

                bool dist = cal_dist(node[i].x, node[i].y, node[j].x, node[j].y);

                if(dist){
                    v[i].push_back(j);
                    v[j].push_back(i);
                }
            }
        }

        // 4. 완전 탐색 수행
        dfs(0);

        // 5. 출력
        // 1) 페스티벌 정점에 도착할 수 있으면 happy 출력
        if(check[n+1]){
            printf("happy\n");
        }
        // 2) 페스티벌 정점에 도착할 수 없으면 sad 출력
        else{
            printf("sad\n");
        }
    }
}