문제

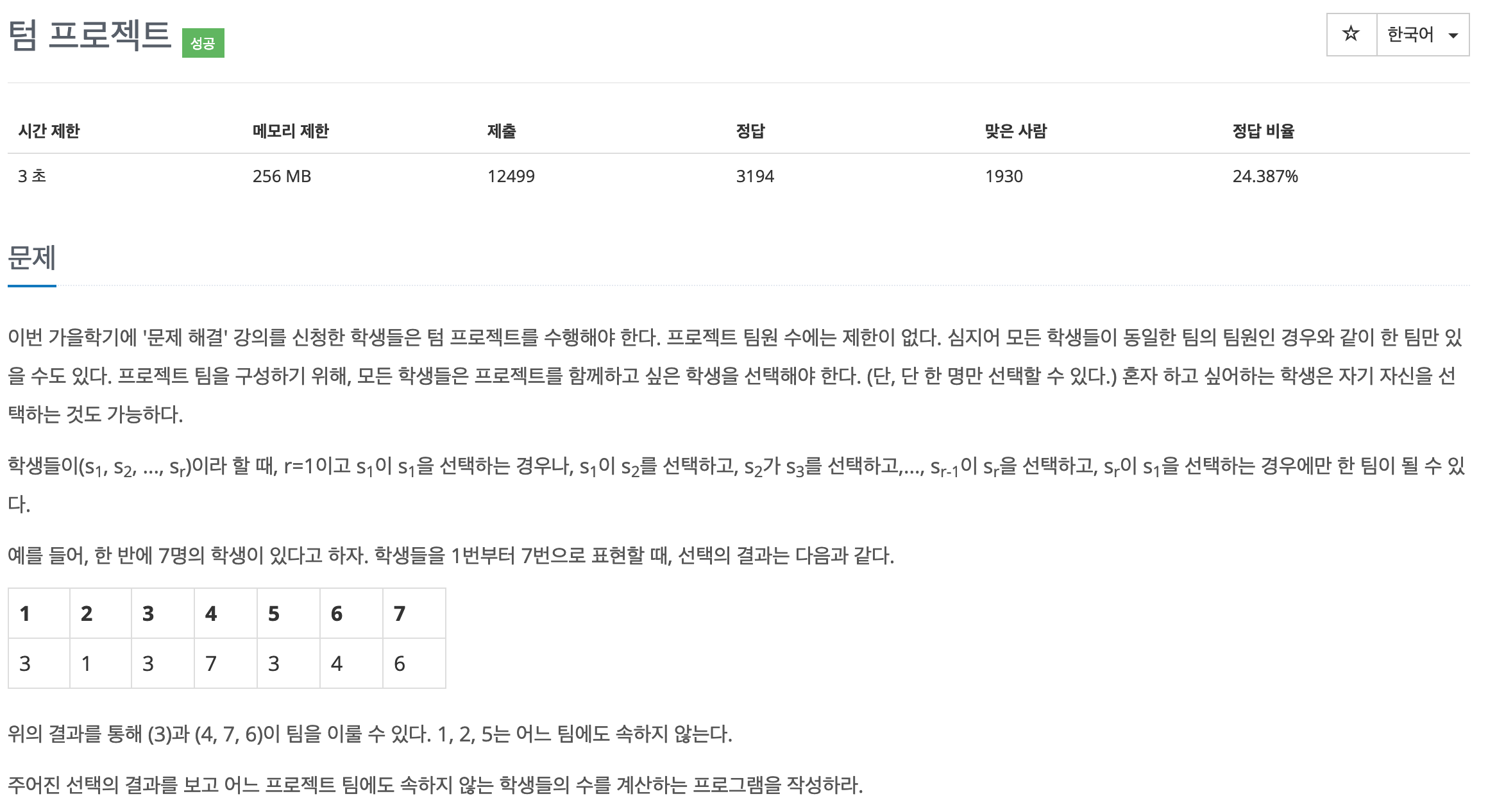
• 1부터 n까지 숫자가 부여된 학생이 n명 있습니다.
• 각 학생이 프로젝트를 함께 하고 싶은 다른 한 사람을 선택했습니다.
• 사이클이 생기면 같은 팀을 할 수 있습니다.
• 어느 팀에 속하지 않은 학생의 수를 구하시오.
• n(1 <= n <= 10만) 학생의 수
• 시간 제한 3초
• 문제 링크

---

접근 과정

1. 사이클, 위상 정렬

• 이 문제는 사이클에 속하지 않는 정점의 수를 구하는 문제입니다. 사이클이 없는 그래프에서 사용할 수 있는 알고리즘으로 위상 정렬이 있습니다. 위상 정렬은 진행 순서를 찾는 알고리즘 입니다. 위상 정렬을 사용해서 사이클에 속하지 않는 정점의 수를 계산합니다.

2. 시간 복잡도 계산

• 1) O(n), 위상정렬의 시간 복잡도는 O(V+E) (V는 정점의 수, E는 간선의 수)
  이 문제에서 V+E = 2n, 상수 생략 O(n)

• n(1 <= n <= 10만) 이기 때문에 O(n)은 O(10만) 문제의 시간 제한이 3초 이기 때문에 시간안에 풀 수 있습니다.

코드

1. C++

#include <iostream>
#include <vector>
#include <queue>

#define max_int 100001

using namespace std;

//시간 복잡도: O(n)
//공간 복잡도: O(n)
//사용한 알고리즘: 위상 정렬
//사용한 자료구조: 인접 리스트

int t, n, num, result;
// 정점 i의 indegree 수를 저장하는 배열
// ind[i]=j, 정점i의 indegree수는 j 입니다.
int ind[max_int];
// 간선의 정보를 저장하는 인접 리스트
vector<int> v[max_int];

// 변수 초기화
void init(){
    result = 0;
    for(int i=0; i<=n; i++){
        ind[i] = 0;
        v[i].clear();
    }
}

int main(){
    scanf("%d", &t);

    // 1. 입력
    for(int test_case=1; test_case <= t; test_case++){
        scanf("%d", &n);

        // 2. 초기화
        init();

        // 3. 간선을 인접리스트에 저장합니다.
        for(int i=1; i<=n; i++){
            scanf("%d", &num);
            v[i].push_back(num);
            // indegree의 수를 갱신해줍니다.
            ind[num]++;
        }

        // 4. 큐에 들어간다는 의미는 사이클에 속하지 않는다는 의미입니다.
        queue<int> q;
        for(int i=1; i<=n; i++){
            if(ind[i] == 0){
                q.push(i);
                result++;
            }
        }

        // 5. 위상 정렬 수행
        while(!q.empty()){
            int node = q.front();
            q.pop();

            for(int i=0; i<v[node].size(); i++){
                int next = v[node][i];

                // indegree를 감소시켜줍니다.
                ind[next]--;

                // indegree가 0이 되면 큐에 넣어줍니다.
                // 큐에 들어간다는 의미는 사이클에 속하지 않는다는 의미입니다.
                if(ind[next] == 0) {
                    q.push(next);
                    result++;
                }
            }
        }

        // 6. 출력
        printf("%d\n", result);
    }
}