시리즈 소개

유클리드 원론 학습의 이익

유클리드 원론이 다루는 내용은 한국의 초등학교와 중학교 교육 과정에 일부 포함되어 있다. 작도, 엇각, 맞꼭지각 등의 개념이 이때 나온다. 이 개념들이 대단히 중요한 내용이라고 생각하는 사람은 드물 것이다. 고등학교 교육 과정에서 좌표를 도입하면서 유클리드 방식의 증명을 폐기 처분하기 때문이다.

그러나 유클리드 원론을 중학교 내신 시험을 치기 위한 수단으로만 사용하는 것은 너무 아까운 일이다. 취미나 교양으로 수학을 배울 때 원론이 최고의 교재 중 하나라고 생각한다. 역사적으로도 유클리드 원론은 2000년이 넘는 세월동안 논리적 사고를 함양하기 위한 필수 교양으로 취급 받았다. 기원전 인물인 프톨레마이오스 왕부터 현대의 에이브라함 링컨, 아인슈타인까지 원론을 배웠다고 한다

유클리드 원론은 '어려운 개념을 암기해 정확하게 문제를 푸는데 집중하는' 방식의 수능 수학과는 정확히 반대이다. '이등변 삼각형의 두 밑각의 크기는 같다.' 와 같이 직관적으로 당연해보이는 내용까지 지나칠 정도로 엄밀하게 증명한다. 유클리드 원론에 포함된 수학적 내용은 대부분 초등학교에서 중학교 과정 사이에 배우는 것이다. 대부분 이미 알고 있는 개념에 대해 증명하므로, 새로운 것을 이해하느라 애쓸 필요는 없다. 증명을 따라가면서 논리적인 사고 방식을 배우는데만 집중하면 된다.

예정 연재 내용

당초 원론의 모든 정의와 정리를 다루는 것을 목표로 했으나, 그렇게 해선 완결이 불가능하다는 결론에 도달하게 되었다. 따라서 내가 흥미를 느낀 내용을 일부 선정해서 연재하기로 계획을 바꾸었다. 연재 순서도 원론의 순서를 따라가지 않을 가능성이 높다. 일부 내용만을 다루고, 순서도 뒤죽박죽인 대신 설명은 상세하게 보강할 예정이다.

유클리드 원론의 구성

정의, 공준, 상식

정의(Definition)란 어떤 용어가 지칭하는 개념이나 대상을 정하는 것이다. 유클리드 원론은 다음과 같은 정의와 함께 시작한다.

1. '점'은 넓이가 없는 위치이다.
2. '선'은 폭이 없는 길이이다.
3. 선의 양 끝은 점으로 이루어져 있다.
4. '직선'은 고르게 놓여있는 점 위에 있는 선이다. (주의: 현대 수학에서의 '선분'을 '직선'으로 정의하고 있다.)
   ...

점을 정의할 때 쓰인 '넓이'나 '위치'의 정의는 무엇인가? 라는 질문이 자연스레 떠오를 수 있다. 넓이를 '2차원 공간에서의 크기' 로 정의한다고 해보자. 다시 2차원은 무엇이고 공간은 무엇이냐는 질문이 나올 수 있다. 마치 기저 사례를 지정하지 않은 재귀함수처럼 끝이 나지 않는다. 그래서 정의에 쓰인 단어를 다시 정의하지는 않는다. 현대 수학에서는 유클리드 원론에서의 '넓이'나 '위치'처럼 정의 없이 사용하는 용어들을 '무정의 용어'라고 하는데, 사이언스올의 과학백과사전에선 이렇게 설명하고 있다.

[요약] 구체적인 정의를 내리지 않고 그 성질을 공리로 규정하는 수학적 개념을 말한다. 수학에서 사용되는 용어들을 정의에 따라 계속 거슬러 올라가다 보면 가장 기초적인 용어가 나오게 되는데 이 가장 기초에 있는 용어는 하나로 정의내리지 않고, 공리를 통해 그저 받아들이게 된다. 이것을 무정의 용어라고 말한다. 예를 들어 정삼각형을 통해 무정의 용어를 찾아보면, 우선 정삼각형의 정의는 세 변의 길이가 같은 삼각형이다. 그렇다면 삼각형의 정의를 찾게 되고 그 다음 선분의 정의를 찾으면 마지막으로 점이 나온다. 점은 따로 정의가 없는 공리이다. 이렇게 다른 용어의 정의에 기초가 되는 용어를 무정의 용어라고 한다.

정의 다음에는 공준(postulate)과 상식(common notion)이라는게 나오는데, 현대적 관점에서 보면 모두 공리(axiom)라고 할 수 있다. 공리란 수학에서 증명을 하지 않고 무조건 참으로 가정하는 명제를 말한다. 왜 증명하지 않고 믿을까? 두 가지 이유가 있다. 첫 번째 이유는 정의와 마찬가지로 증명을 증명하는 무한 루프에 빠질 수 있다는 것이다. 두 번째 이유는 수학을 연구하는 이유가, 특정한 공리들이 참일 때 어떤 명제를 증명할 수 있는지가 궁금해서이기 때문이다.

예를 들어 어떤 사람들이 로또 복권에 당첨되면 무엇을 하고 싶은지 이야기 하고 있다고 하자. '로또 당첨은 가능성이 극히 낮은 일이다.' 라는 지적은 타당하지만 이들의 관심사가 아니다. 이는 공리를 종교처럼 무조건 믿으란 말은 당연히 아니다. '만약 이런 일이 일어난다면~' 이라는 대화의 주제는 로또 복권 말고도 원하는 무엇이든 고를 수 있다. 마찬가지로 공리도 본인이 원한다면 빼거나 더해서 새로운 수학의 시작점인 공리계를 만들 수 있다. 대표적인 사례로 유클리드 기하학의 근간인 평행선 공준도 이를 빼고 싶어한 수학자가 있어 비유클리드 기하학이 탄생했다.

공준과 상식은 현대적 관점에서 보면 모두 공리이지만 다소 어감의 차이가 있다. 기하학적 대상에 대한 공리를 다룬 공준과 달리, 상식은 모든 수학적 대상에 통용되는 명제이다. 예를 들어 공준에는 '한 점에서 다른 점으로 선을 연결할 수 있다.', '특정 점을 기준으로 원을 그릴 수 있다.'와 같은 명제가 포함된다. 상식은 '같은 것에서 같은 것을 빼면 남은 것도 같다.', '전체는 일부보다 크다' 와 같이 훨씬 추상적이다.

명제

명제(proposition)의 현대적 정의는 '참, 거짓을 논리적으로 증명할 수 있는 문장이나 표현'인데 원론에서도 같은 뜻으로 쓰이고 있다고 보아도 무방하다. (무방하다는 표현을 쓰는 이유는 명제가 무엇인지 직접 정의하는 내용이 없기 때문이다.) 공준이나 상식과는 달리, 명제로 인정 받으려면 반드시 증명이 있어야 한다. 그리고 그 증명에서는 정의, 공리, 그리고 이미 증명한 다른 명제만을 이용한다. 이렇게 다른 명제를 밝히는 데 주요한 역할을 한다는 점에서 사실상 현대 수학의 정리(theorem)의 역할과 같다고 볼 수 있다.

현대 수학과 조금 다른 점은 작도(눈금 없는 자와 컴퍼스만을 이용해 원하는 도형을 그리는 것) 방법도 명제라고 지칭한다는 것이다. 예를 들어 유클리드 원론의 첫 명제는 정삼각형을 작도하는 방법이다. 작도 방법도 정의, 공리, 다른 명제만을 이용해서 증명하는 것은 똑같다. 물론 현대 수학의 관점에서 보면 다소 논리의 비약으로 보이는 지점도 있긴 하지만, 최대한 엄밀한 증명을 하려는 태도로 임했다는 것은 분명하다.

명제의 예: 정삼각형의 작도

책 소개만 하고 끝나기엔 아쉬우니 유클리드식 증명의 예를 하나 살펴보자. 유클리드 원론 1권은 23개의 정의, 5개의 공준, 5개의 상식이 나온 후 48개의 명제가 소개된다. 그 중 첫 명제가 정삼각형의 작도 방법이다.

배경 지식

우선 정삼각형의 작도 증명에 사용된 정의와 공준은 다음과 같다. 정의는 Def, 공준은 Post, 상식은 CN으로 표기한다. 로마자로 표기한 숫자는 권수를 나타낸다. 예를 들어 I.Post.3은 원론 1권의 공준 3번이다.

• I.Def.1: 점(point)이란, 넓이가 없는 위치이다.
• I.Def.2: 선(line)은 폭이 없는 길이이다.
• I.Def.3: 선의 양 끝은 점(point)으로 이루어져 있다.
• I.Def.4: 직선(straight line)이란, 그 위에 있는 점들과 고르게 놓여 있는 선이다. (주의: 유클리드 원론에서는 직선, 반직선, 선분을 모두 직선이라고 표현한다.)
• I.Def.15: 원(circle)이란, 하나의 선으로 둘러싸인 평면 도형으로서, 그 도형 안의 한 점으로부터 그 선에 이르는 모든 직선의 길이가 서로 같은 도형이다.
• I.Def.16: 그리고 그 한 점을 원의 중심(center)이라고 부른다.
• I.Def.17: 지름(diameter)이란 원의 중심을 지나면서 원의 둘레에 의해 양쪽 끝이 정해진 어떤 직선이다. 그리고 이러한 직선은 원을 양분한다.
• I.Def.19: 직선 도형(rectilinear figures) 이란 직선들로 둘러싸인 도형이다. 이 중 세 개의 직선으로 이루어진 도형은 삼각형(trilateral figure), 네 개로 이루어진 도형은 사각형(quadrilateral figure), 네 개를 초과하는 경우는 다각형(multilateral figure) 이라 한다.
• I.Def.20: 삼각형 중 세 변이 모두 같은 것은 정삼각형(equilateral triangle),
  두 변만 같은 것은 이등변삼각형(isosceles triangle),
  세 변이 모두 다른 것은 부등변삼각형(scalene triangle)이라 한다.
• I.Post.1: 임의의 두 점을 잇는 직선을 그릴 수 있다.
• I.Post.3: 임의의 중심과 반지름으로 원을 그릴 수 있다.
• CN.1: 같은 것과 같은 것은 서로도 같다. (쉽게 말해 x=y 이고 y=z이면 x=z 라는 뜻이다.)

증명

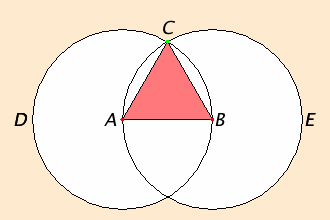
주어진 직선 AB와 같은 길이의 변으로 구성된 정삼각형을 작도하는 방법이다.

• A를 중심으로 하고 AB의 길이를 반지름으로 하는 원 BCD와 B를 중심으로 하고 AB의 길이를 반지름으로 하는 원 BCE를 그린다. (I.Post.3)
• 두 원이 만나는 점 C에서 점 A와 B까지 직선 CA, CB를 그린다. (I.Post.1)
• 점 C와 B는 모두 원 BCD를 이루는 선 위에 있다. 따라서 원의 중심인 A와 연결된 AC, AB의 길이는 같다. 마찬가지로 BC, BA의 길이도 같다. (I.Def.15)
• AC=AB 이고 AB=BC 이므로 AC=BC이다. 따라서 AB와 AC와 BC는 모두 같다. (CN.1)
• 삼각형 ABC는 주어진 직선 ABC 위에 작도된 정삼각형이다.(I.Def.20)

비판

앞서 유클리드는 엄밀한 증명을 하려 노력했지만 현대적 관점에서는 아쉬운 점도 있다고 했다. 이 증명은 원론의 첫 번째 명제인만큼 오랜 세월동안 비판에 직면했는데, 대체로 명제 1을 증명하기 위해 암묵적으로 참이라고 가정한 명제가 있다는 내용이다. 이 증명은 다음의 명제들을 암묵적으로 참이라고 가정해야 성립한다. 다행히도 우리의 직관과 크게 어긋나지 않는다.

교점 C가 존재한다

고등학교 1학년 수학에서 두 원의 위치 관계에 대해 배운다. 대략 다음과 같은 내용이다.

점 a를 중심으로 하는 원 A, 점 b를 중심으로 하는 원 B가 있고 A의 반지름을 r, B의 반지름을 r'이라 하자. a와 b의 거리를 d라 할 때

• r+r' < d: 원의 교점이 없다.
• r+r' = d: 한 점에서 만난다.
• r-r' < d < r+r' d: 두 점에서 만난다.

그런데 원론에는 원의 위치 관계를 정의하는 공준이 없다. 따라서 원 BCD와 BCE가 교점을 가질거라는 보장을 할 수 없다.

두 직선의 교점 C가 두 원의 교점이기도 하다

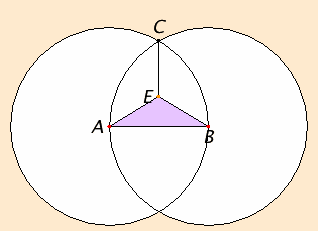
다음 그림과 같이 A와 B에서 그어진 선이 C에 도달하기 전 E라는 다른점에서 만난다면 이 명제는 성립하지 않는다. 마찬가지로 원의 위치 관계를 받아들여야 C가 두 원의 교점이라는 사실이 증명된다. (원의 위치 관계를 받아들이면 교점은 두 개가 나온다. 하지만 두 점 중 어느 곳으로 직선을 긋더라도 정삼각형이 된다.)

삼각형 ABC는 평면 도형이다.

ABC의 모든 직선이 동일한 평면 위에 그려지지 않았다면, 즉 입체 도형이라면 이 정리는 성립하지 않는다. 또 세 직선 중 하나라도 시작점이 있는 평면과 종료점이 있는 평면이 다르다면 이 정리는 성립하지 않는다.

왜 성립하지 않는지를 증명하는 것은 나의 능력을 넘어선다. 하여튼 그렇다는 것이 증명되었다고 하니 찜찜한 사람들은 각자 찾아보길 바란다.

참고 자료

• 원론의 모든 텍스트 및 이미지 출처: http://aleph0.clarku.edu/~djoyce/java/elements
• 번역: ChatGPT