
접히는 컴퍼스(Collapsing compass)의 정의
작도란 종이 위에 원하는 도형을 그리는 알고리즘이다. 단 컴퍼스와 눈금 없는 자만을 이용해야 한다. 자에 눈금이 없으니 길이를 잴 수 없다. 그래서 첫 번째 정리에서 작도한 삼각형이 정삼각형이라는 점을 증명하기 위해 원이 두 개나 필요했던 것이다. 자에 눈금이 있었다면 세 선분의 길이를 자로 직접 비교 했으면 됐을 것이다.
그런데 사실 선분의 길이를 비교하는 것은 자에 눈금이 없어도 가능하다. 우리에겐 컴퍼스가 있기 때문이다. 실제로 중학교 수학에서는 주어진 선분과 같은 길이의 선분을 작도하는 법을 다음과 같이 가르치고 있다.
- 컴퍼스의 두 다리를 이용해 선분의 길이를 잰다.
- 다리 사이에 자를 대고 선분을 그린다.
그런데 원론에서 가정하는 컴퍼스에는 길이를 재는 기능이 없다. 컴퍼스를 종이에서 떼자마자 바로 다리를 접어버리는 것으로 가정한다. 이러한 컴퍼스를 접히는 컴퍼스(Collapsing compass) 라고 지칭한다. 컴퍼스의 다리가 바로 접히므로 앞서 소개한 방식의 선분의 길이 복사가 불가능하다.
접히는 컴퍼스를 다음의 사진과 같이 실에 연필을 묶어 만든 컴퍼스에 비유하기도 한다. 실과 연필을 종이에서 떼는 순간 기존의 길이를 보존할 수 없게 된다.

접히는 컴퍼스를 사용하는 이유
사실 접히는 컴퍼스를 사용하더라도 선분의 복사는 충분히 가능하다. 원론 1권의 두 번째 증명은 컴퍼스 동등 정리(Compass equivalence theorem)라고 불리기도 한다. 접히는 컴퍼스로도 현대 컴퍼스가 할 수 있는 작도를 모두 할 수 있다는 의미다.
하지만 굳이 왜 이런 짓을 해야 하는지에 대한 의문이 남는다. 유클리드는 현대적 컴퍼스를 만들 줄 몰라서 실에 연필을 묶어 사용했던 것일까? 그렇다 하더라도 왜 현대의 우리까지 접히는 컴퍼스를 위해 복잡한 증명을 이해해야 하는 것일까? 그 이유는 수학자들이 이런 종류의 불편을 즐기기 때문이다. 생산성을 중시하는 개발자들에게는 이해가 가지 않을 수 있다.
앞선 글에서 소개한 것처럼, 유클리드 원론의 정리(명제)에는 작도도 포함되어 있다. 작도가 정리라면 눈금없는 자와 컴퍼스의 존재는 공리라고 할 수 있다. 그런데 예나 지금이나 수학자들은 공리가 너무 많은 것을 좋아하지 않는다. 앞서 수학은 공리가 참일 때 증명할 수 있는 명제들을 찾는 활동이라고 했다. 그런데 다른 공리로부터 충분히 증명 가능한 사실을 공리로 설정하면 재미있는 게임을 핵이나 치트로 망치는 셈이 된다. 유클리드를 포함한 고대 철학자들은 이 작도라는 게임에 꽤 진심이었다.
배경 지식
이 정리를 증명하기 위해 다음의 개념이 사용된다. I-N 과 같은 표기는 1권의 N번 명제라는 뜻이다.
(앞 시리즈에서 이미 설명한 내용은 설명을 생략했다.)
- I.Def.15: 원(circle)이란, 하나의 선으로 둘러싸인 평면 도형으로서, 그 도형 안의 한 점으로부터 그 선에 이르는 모든 직선의 길이가 서로 같은 도형이다.'
- I.Post.1: 임의의 한 점에서 다른 점을 연결하는 직선을 그릴 수 있다.
- I.Post.2: 주어진 유한 직선을 연장할 수 있다.
- I.Post.3: 임의의 중심과 반지름으로 원을 작도할 수 있다.
- CN.3: 같은 것에서 같은 것을 빼면 남는 것도 같다. (쉽게 말해 x=y 이면 x-z=y-z라는 뜻이다.)
- I-1: 정삼각형의 작도 방법
컴퍼스 동등 정리
주어진 직선 BC와 같은 길이의 직선을 그리는 방법은 다음과 같다.
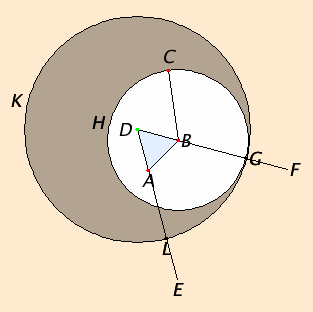
- 점 B와 임의의 점 A를 연결한다. (I.Post.I)
- BA와 같은 길이의 직선들로 구성된 정삼각형 BAD를 작도한다.(I-1)
- DA와 DB를 연장해 직선 AE, BF를 작도한다. (I.Post.2)
- B가 중심이고 BC가 반지름인 원 BGH를 작도한다. G는 원 BGH를 이루는 점 중에서, 직선 BF 상에 있는 점이다. (I.Post.3)
- D를 중심으로 하고 DG가 반지름인 원 GKL을 작도한다. L은 원 GKL을 이루는 점 중에서 직선 AE상에 있는 점이다.
- C와 G는 모두 B를 중심으로 하는 원 BGH를 구성하는 점이다. 따라서 BC의 길이는 BG와 같다. 한편 G와 L은 모두 D를 중심으로 하는 원 GKL을 구성하는 점이다. 따라서 DG의 길이는 DL과 같다. (I.Def.15)
- DL=DG이고 DA=DB이므로 AL=BG이다. (CN.3)
- 6번에서 밝혔듯이 BG=BC 이므로 AL=BC이다. 따라서 AL은 직선 BC와 같은 길이의 직선이다. (CN.1)
여러 단계를 거쳐서 주어진 직선과 같은 길이의 직선을 작도했다. 이후로는 같은 길이의 직선을 그릴 필요가 있을 때 '정리 2에서 증명한 방식대로 같은 길이의 직선을 작도한다.' 는 식으로 넘어간다.
비판
이 정리도 오랜 세월동안 증명의 엄밀성에 대한 비판이 있었다고 한다. 주로 이 증명이 모든 경우의 수에 대해서가 아니라 도형이 특수한 형태로 배치된 상황에서만 성립된다는 비판이었다. 그러나 이는 서구권에 퍼진 번역에 누락된 것이 생긴 비판이라고 한다. 이에 대해 서술한 논문인 'A New Look at Euclid's Second Proposition'을 참고 자료에 첨부하였다.
참고 자료
- 친절한 보선쌤, 길이가 같은 선분의 작도
- Rise over Run Math,
Geometric Constructions: Drawing a Circle with a String - Godfried Toussaint, A New Look at Euclid's Second Proposition
