Data Structures

데이터를 다룰때 사용하는 특정형태 - 어떤 상황이 가장 적합한지 찾는다면 최적화된 코드를 짤 수 있다.
언어에 국한되지 않고 보장되어 있다.

Big O를 항상 생각하고 코드에서 구분한다.

Stack (Last-In First-Out)

---

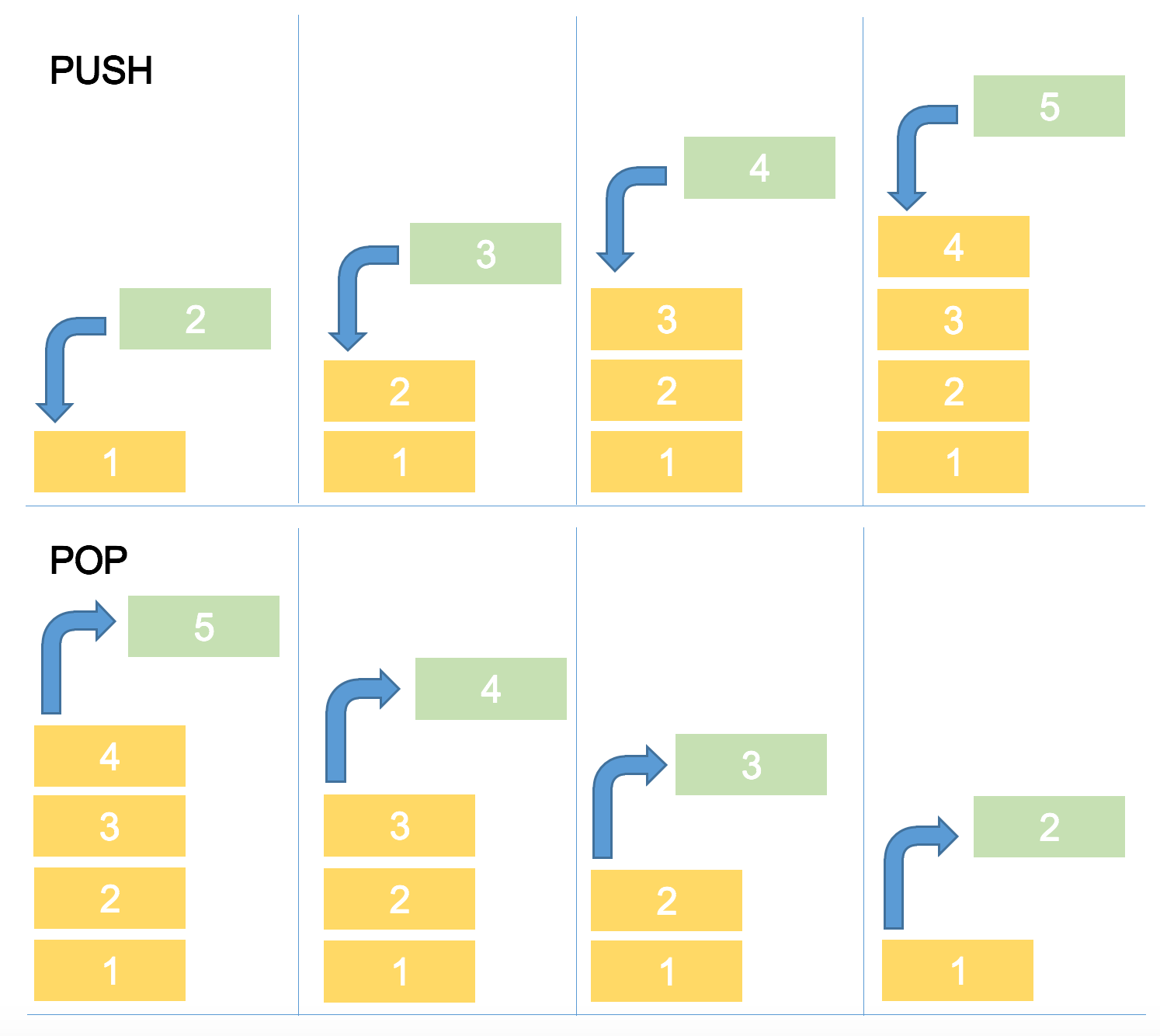
자료를 추가했다가 뺐다가 한다.
맨 마지막으로 들어간게 첫번째로 나온다. - Last-In First-Out

• Push: 자료를 추가를 한다. 책을 쌓아가는 방식으로 하나하나 쌓인다고 생각하자
• Pop: 자료를 뺀다. - 쌓인 책이 쓰러지지 않도록 위에서부터 빼낸다.

Big O

수학적인 표기법을 말한다.
Big O란 표기법의 하나로 시간,공간의 복잡도를 설명해준다.

Time Complexity	Average	Worst
Insertion	O(1)	O(1)
Deletion	O(1)	O(1)
Search	O(n)	O(n)

Insertion, Deletion: 괄호의 1은 상수를 말한다. 항상 1이다. 시간적인 소요가 항상 같다. 삽입하거나 삭제하면 끝, 그 외에 고려할 사항이 전혀없다. 연산을 한 후 삽입과 제거를 하는것이 아니다.
Search: n은 상황에 따라 다르다. stack의 사이즈.어디에 있는지 알 수 없기 때문이다.

Real Life Use Cases

• 재귀함수
• Undo/Rodo Mechanism - 에디터를 사용했을 때를 예시로 들 수 있다.
• Backwards/Forwards Mechanism of Browsers
• Call Stack
• matching Brackets 알고리즘 - {}() 이런식의 짝이 맞는지에 대한 알고리즘

Queue (First-In First-Out)

---

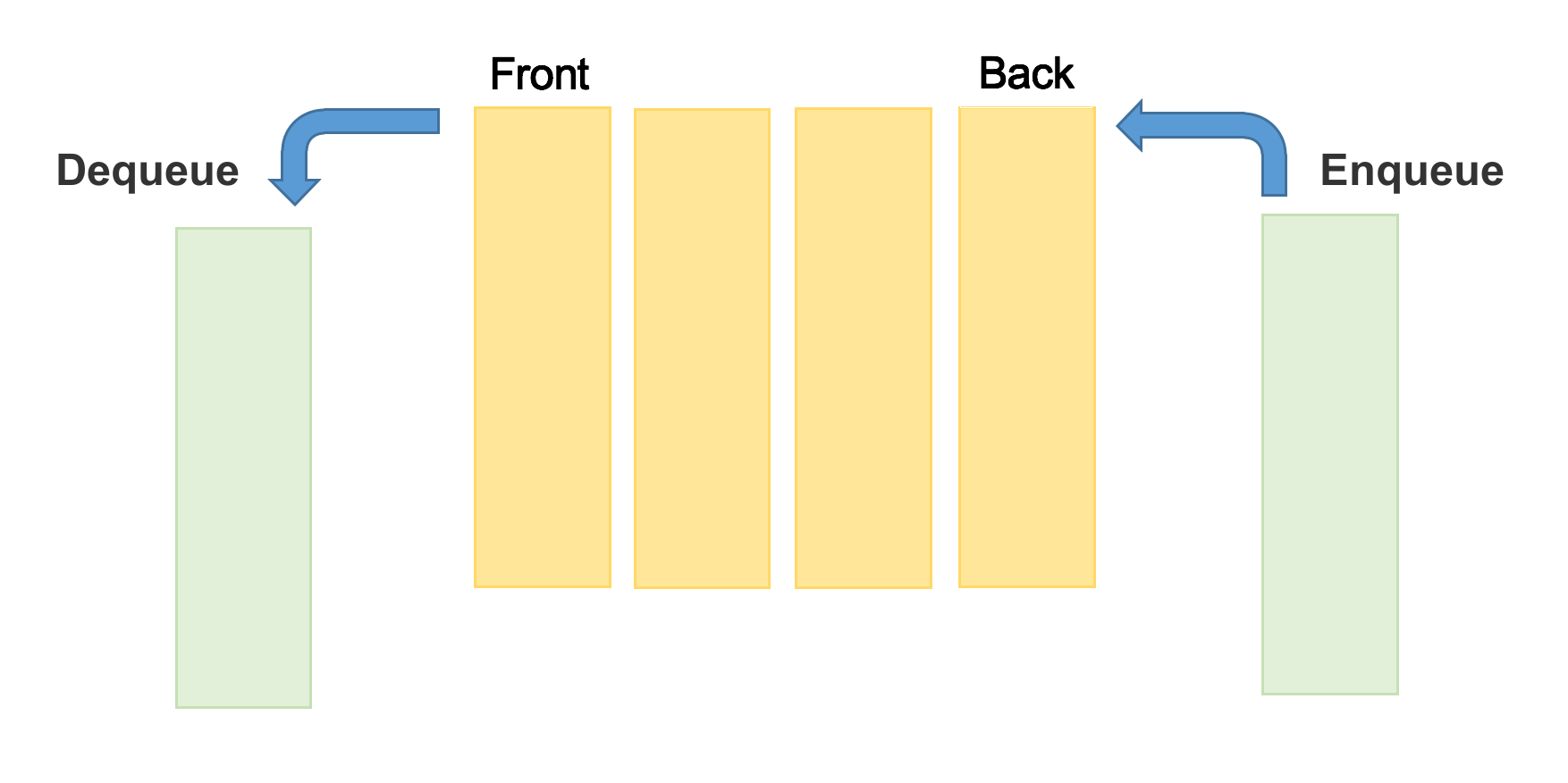
사람들이 줄서는거랑 비슷하다.

• Enqueue: 앞에서 부터 차례대로 세운다.
• Dequeue: 앞에서 부터 차례대로 빠진다.

Big O

변수가 없다.

Time Complexity	Average	Worst
Insertion	O(1)	O(1)
Deletion	O(1)	O(1)
Search	O(n)	O(n)

Insertion, Deletion: 변수가 없다. 중간에 있는걸 삽입이나 삭제하는 경우 찾는거와 제거하는거같이한다 하여도 삽입과 제거만 생각한다.
Search: n은 상황에 따라 다르다. stack의 사이즈.어디에 있는지 알 수 없기 때문이다.

Real Life Use Case

• Life of people standing for food
• Callback queue

Linked List 연결 리스트

---

이미지 출처 - w3schools

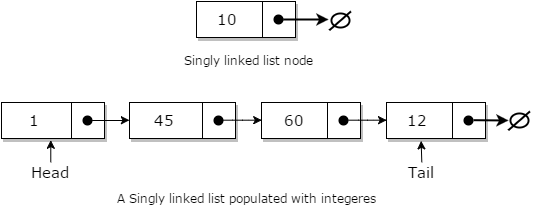
• next를 인지하고 있다.
• 오직 내 뒤에 누가 있는지 인지 한다.
• 스택큐는 인지하지 않는다.
• 맨 첫번째는 head고 맨 마지막은 tail이라 부른다.
• 배열과 다르다.
• 연결되어 있다.

Big O

Time Complexity	Average	Worst
Insertion	O(1)	O(1)
Deletion	O(1)	O(1)
Search	O(n)	O(n)

Insertion: 어떤 자리에 꽂던 앞의 꼬리를 연결하고 뒤에 꼬리를 연결한다.
Deletion: 삭제한 후 앞의 꼬리와 뒤의 꼬리를 연결한다.
Search: 앞에서부터 시작한다. next를 기억하고 있기 때문이다.

Real Life Use Case

• The history section of web browers
• Line of people standing for food

Linked List vs Array

참고 링크

차이	Array	Linked List
Access	index를 통해 빠르게 접근	Array보다 느리다.
삽입 삭제	느리다	빠름
크기	고정	유동적
메모리 요구 사항	인덱스에 실제 데이터가 저장되기 때문에 적다.	next를 참조하기 때문에 더 많은 메모리가 필요하다.

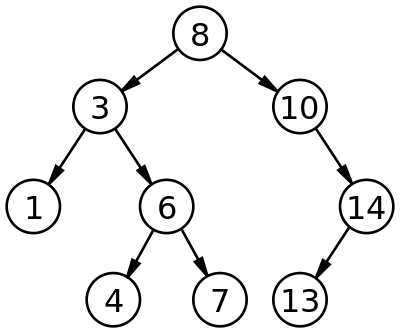
Tree

---

• 부모 자식 관계를 가진다.
• 계층이고 그룹을 가진다.
• node는 하나 이상의 child를 가질 수 있다.
• 부모를 아는 경우도 있고 자식만 아는 경우도 있다.
• 특정한 순서가 있을 수도 없을 수도 있다.
• 시작점을 Root라고 한다.
• 더이상 자식이 없는 경우 leap 잎사귀라 부른다.

node

• 하나의 구성요소 (어디서든지 쓰일 수 있다.)

트리 종류

• Binary Tree(이진트리): 자식을 두개까지 갖는다.
• Ternary Tree: 세개
• Binary Search Tree(이진검색트리):
  • 자식을 최대 두개까지 가질 수 있다. (Binary Tree와 동일)
  • 왼쪽자식노드는 부모노드보다 작아야 하고 오른쪽자식노드는 커야한다. (Binary Tree와 차이점)
  • 왼쪽부터 채워나간다.
• Perfect Binary Tree: 완벽쓰

Real Life Use Case

• 회사나 정부의 조직 구조
• 나라, 지방, 시•군별, 계층적인 데이터의 저장
• 컴퓨터 파일 시스템과 같이 계층을 형성하는 정보를 저장하기 위해 사용
• DOM
• File System

Hierarchical Data(계층구조)가 특징이다.

Binary Search Tree

---

wikipedia 출처

Big O

Time Complexity	Average	Worst
Insertion	O(log(n))	O(n)
Deletion	O(log(n))	O(n)
Search	O(log(n))	O(n)

What does the time complexity O(log n) actually mean?

link

Insertion과 Deletion은 o(1)이 아니고 o(log(n))인 이유

트리는 전체가 유기체라 서로 떼놓을 수 없는 관계이기 때문에 o(log(n));
삭제할 때 루트와 계속 값을 비교해야하기 때문에 하나의 유기체라고 할 수 있는 것이다.

Worst에서 O(n)인 이유는?

Runestone Academy 출처

트리가 양쪽으로 나뉘어져 있는게 아니라 일렬과 비슷한 모양을 가질때다.
이 같은 문제점을 피할 수 있는 방법은
AVL Tree, Red Black Tree(trie) - 한쪽으로만 쏠리는 상황을 피할 수 있다. self-balancing을 가지고 있다.

Real Life Use Case

• 순서가 있는 자료 - 키 순서

What is the difference between a binary tree and a binary search tree?

link

• binary tree - 자식을 두개 까지 갖는다.
• binary search tree - 왼쪽이 작은값, 오른쪽이 큰 값을 갖는다.

Set

---

• 순서가 없다. 오직 자료가 있냐 없냐만 중요하다.
• 집합이므로 중복된 데이터가 들어갈 수 없다.
• 중복되지 않은 숫자(데이터)를 구할 때 사용하면 유용하다.
• 빠른 속도

Real Life Use Case

• 하루 접속자 카운트 - 중복된 ip는 삭제한다.

Hash Table

---

출처 - wikipedia

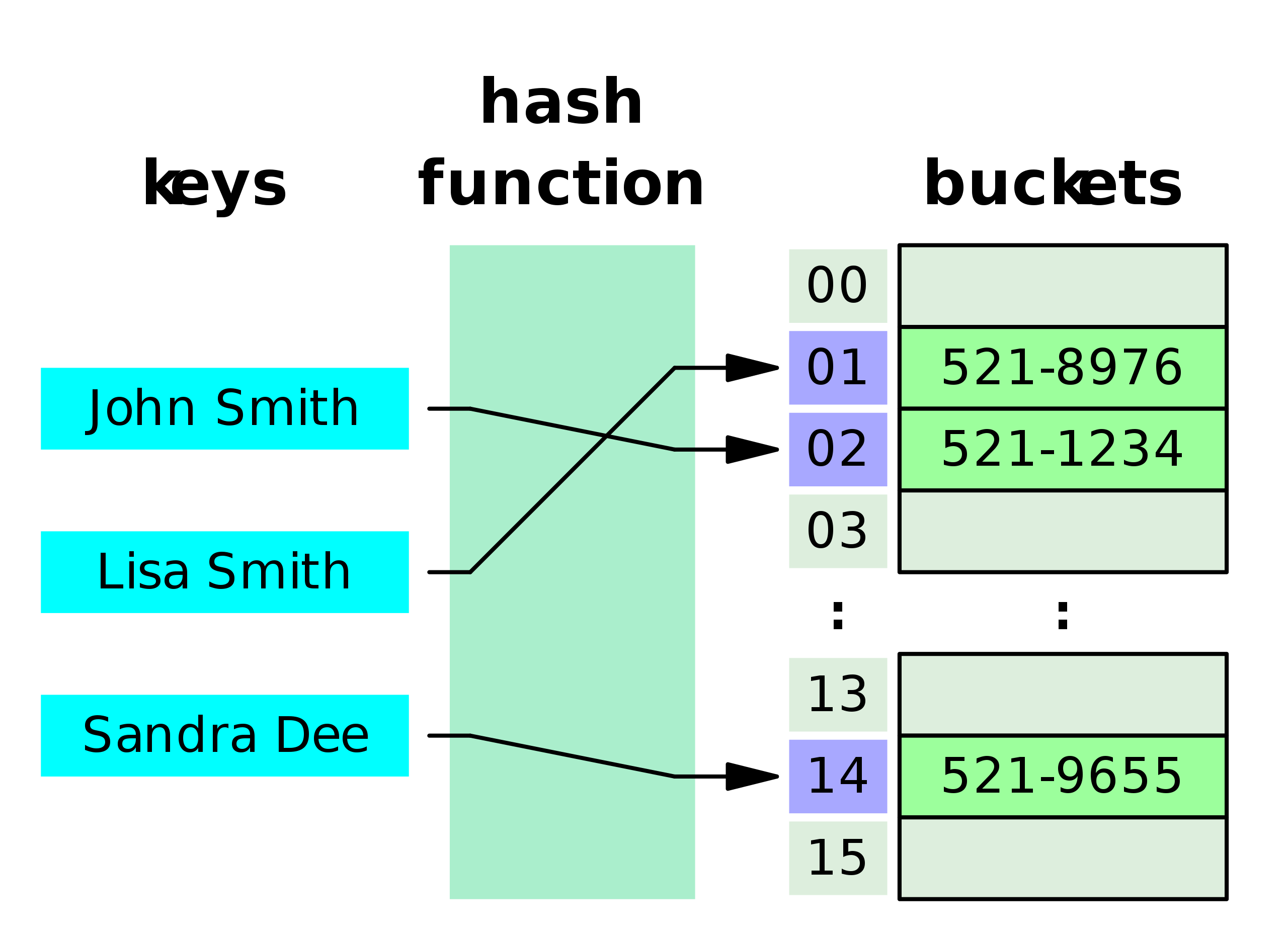
Extrememly Important - 가장 중요한 것 중에 하나다.

F(key) -> HashCode -> Index ->  Value

1. 검색하고자 하는 Hash key를 hsah 함수(F(key))에 넣고, 반환 받은것이 HashCode
2. HashCode를 배열의 Index로 환산을 한다.
3. 데이터에 접근하는 자료구조이다.

key: 문자나 파일데이터나 숫자 등이 될 수 있다.

재정리

1. 데이터가 있다.
2. 해시 함수를 통해 함수안에 규칙,알고리즘으로 데이터들은 Hash Code를 갖는다.
3. 해시코드는 index가 되어 자료를 찾는다.

• key 값이 얼마나 큰지 상관없이 동일한 HashCode로 만들어 준다.

모든 사람들이 모든 거래장부를 다 갖고 있다. 그건 너무 크기때문에 HashCode로 가지고 있는다.

Hash Algorithm

방을 나눌때 노는 방이 없도록 방을 잘 만들어야 한다.

collison(충돌)

 검색시간이 O(1) 만큼 걸리는데 방을 잘못만들면(collison이 많을 경우) O(n)만큼 걸린다.

서로다른 key값으로 동일한 hashcode를 만들기도 한다. 왜냐면 hashcode는 유한하기 때문이다.
다른 코드지만 같은 index방을 받을 수 있다.

장점

• 검색속도가 매우 빠르다. 리소스를 포기하고 속도를 선택했다.
  • 해시함수를 이용해서 만든 해시코드는 정수다. 배열공간을 고정된 크기만큼 만든다. 해시코드를 배열의 나머지연산을 한 만큼 나눠 갖는다.
  • 해시코드 자체가 배열방의 index로 사용된다.
  • 배열에 해시코드로 바로 다이렉트로 접근하기 때문에 빠르다.

단점

• 랜덤하게 넣기 때문에 깔끔하게 정리되지 않는다.
• 공간효율성이 떨어진다. 공간크기를 무조건 정해야한다.
  • 사람, 자리로 생각한다면 사람 < 자리가 항상 커야하기 때문이다.
• Hash Function의 오존도가 높다.

What is hashing?

문자열을 받고 정해진 길이의 아웃풋을 준다.

ex) MD5, SHA and etc.. 유명한 해쉬/ 알고리즘 이름이다.

Hash Function

• 해시함수는 Idempotent(연산을 여러번 해도 달라지지 않는 성질) 여야 한다.

function hash (k) {
  return 2 * k;
}

인풋에 관해 같은 아웃풋이 나와야 한다.

• good distribution of values
  • 확보한 공간을 고루고루 잘 이용해야 한다.
• needs to be performant O(1) 이라는 의미가 확실하도록 해야한다.

Big O

Time Complexity	Average	Worst
Insertion	O(1)	O(n)
Deletion	O(1)	O(n)
Search	O(1)	O(n)

Worst가 O(n)인 이유
검색시간이 O(1) 만큼 걸리는데 해시 테이블의 공간을 잘못 만들면(collison이 많을 경우) O(n)만큼 걸린다.

Real Life Use Case

• 주소록
  • 랜덤하게 저장했다가 뽑아 올 수 있어야 한다.
  • 개별적으로 관계가 없다. 동일 이름은 충돌할 수 있다.
• 블록체인
• 자바스크립트로 객체로 만들었을때 자바스크립트 실행 엔진에서 key와 value를 Hash Function으로 구현되어 있다.
• 유튜브에 영상을 다운 받아서 올린다면 영상데이터 안에 고유의 key값을 가지고 있기 때문에 저작권침해를 알아낼 수 있다.