머신러닝을 공부할 때 개념을 완벽히 알기 보다는, 개념을 인지한 후 그것을 사용했을 때 결과가 어떻게 되는지 아는 게 더 중요할 수도 있다. 개념이 무수히 많기 때문이다.
1. PCA란?
- 데이터 집합 내에 존재하는 각 데이터의 차이를 가장 잘 나타내는 요소를 찾는 방법
- 데이터의 분산을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아, 고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법
- 데이터 압축(차원축소), 변수 추출, 노이즈 제거 등에 활용
- 변수 추출(Feature Extraction)은 기존 변수를 조합하여 새로운 변수를 만드는 기법으로, 변수 선택(Feature Selection)과 다름
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
rng = np.random.RandomState(13)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
X.shape
>>>
(200, 2)🍳
# 평균 0, 표준편차 1인 정규분포를 따르는 숫자를 2 * 2로 나열
rng.rand(2, 2)
>>> array([[0.60735693, 0.79695268],
[0.81266616, 0.26598051]])
# 평균 0, 표준편차 1인 정규분포를 따르는 숫자를 2 * 3으로 나열
rng.rand(2, 3)
>>> array([[0.66338872, 0.91787788, 0.57581744],
[0.24221232, 0.00560409, 0.70730484]])
# 두 행렬의 곱
np.dot(rng.rand(2, 2), rng.rand(2, 3))
>>> array([[0.71715059, 0.72655532, 0.75266935],
[1.09391731, 1.23387105, 0.89297986]])
# 전치
np.dot(rng.rand(2, 2), rng.rand(2, 3)).T
>>> array([[0.59843737, 0.71434027],
[0.30869995, 0.44908286],
[0.36523226, 0.42264424]])plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal') # 두 축을 같은 간격으로 그리기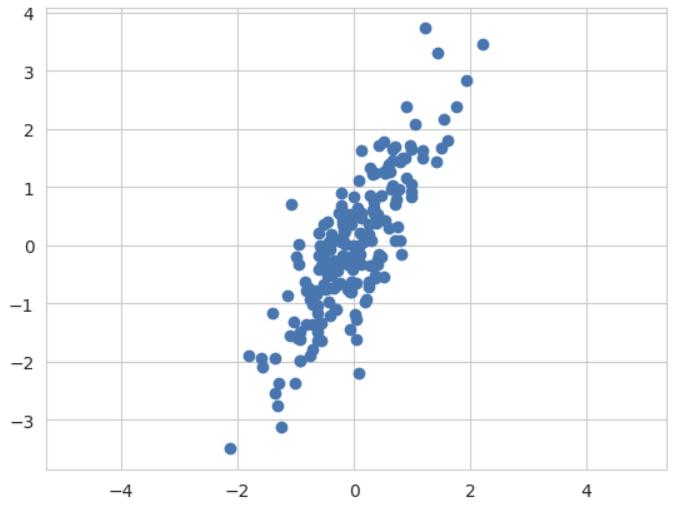
2. 주성분 벡터 그리기
from sklearn.decomposition import PCA
# n_components : n개의 주성분으로 표현
pca = PCA(n_components=2, random_state=13)
pca.fit(X)
# 데이터 X를 설명하는 벡터 2개
pca.components_
>>> array([[ 0.47802511, 0.87834617],
[-0.87834617, 0.47802511]])
# components의 첫 번째 벡터에 대해 1.82531406 만큼 설명력을 가짐
pca.explained_variance_
>>> array([1.82531406, 0.13209947])
# 첫 번째 벡터가 전체를 93% 정도로 설명하고 있음
pca.explained_variance_ratio_
>>> array([0.93251326, 0.06748674])# sklearn 튜토리얼 참고
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca() # ax=None이면 ax=plt.gca(), 아니면 ax=ax
arrowprops = dict(arrowstyle='->', linewidth=2, color='black',
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
plt.scatter(X[:, 0], X[:, 1], alpha=0.4) # alpha : 투명도
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v) # pca.mean_ : 데이터의 중심
plt.axis('equal')
plt.show()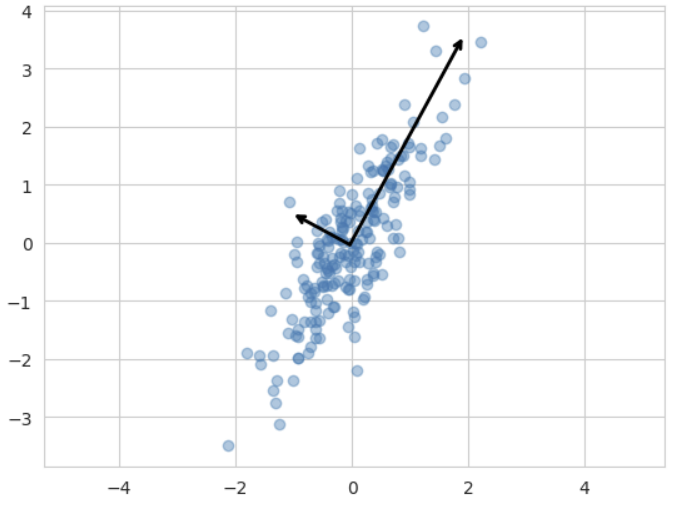
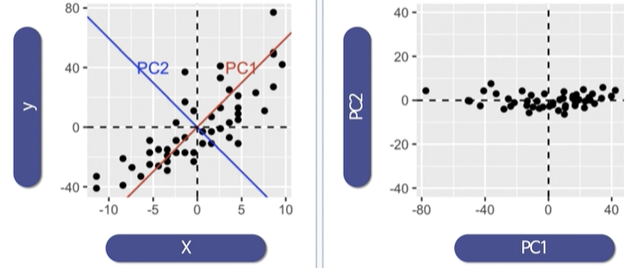
데이터의 주성분을 찾고 나면 주축을 주성분으로 변경할 수 있다.
이때 원래 있던 특성은 사라진다.
3. n_components=1
pca = PCA(n_components=1, random_state=13)
pca.fit(X)
print(pca.components_) ➡ [[0.47802511 0.87834617]]
print(pca.explained_variance_) ➡ [0.93251326]# 원본 데이터
X
>>> array([[-1.07103225e-01, -3.31411265e-01],
[ 3.61221011e-01, 4.12447007e-01], ...
# pca를 적용한 데이터
X_pca = pca.transform(X)
>>> array([[-2.95245605e-01],
[ 5.81990204e-01], ...# X_pca를 2차원으로 변행해서 그래프로 나타냄(같은 차원의 수로 맞춰줌)
X_new = pca.inverse_transform(X_pca)
# 원본 데이터(파란색)
plt.scatter(X[:, 0], X[:, 1], alpha=0.3)
# 주성분이 1개인 데이터로 환원시킨 것 - 직선에 모여 있음(주황색)
plt.scatter(X_new[:, 0], X[:, 1], alpha=0.9)
plt.axis('equal')
plt.show()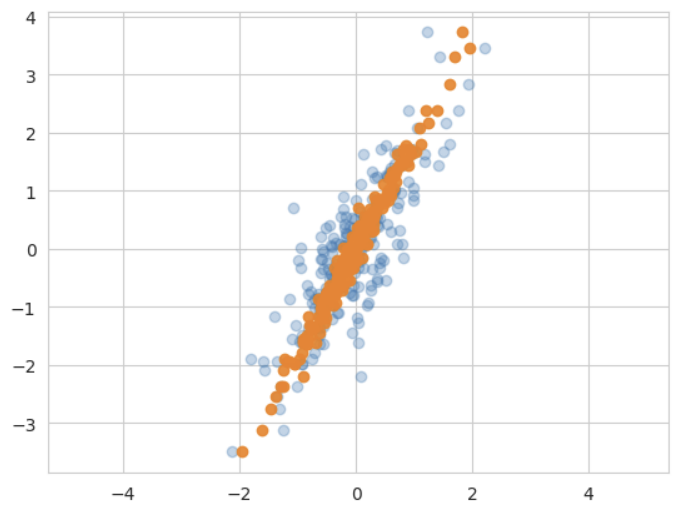
PCA 알고리즘을 통해서 2차원 데이터를 1차원으로 바꾸고, 이를 다시 2차원 표현으로 바꿔서 원본 데이터와 비교한 것이다.
