
딥러닝, 머신러닝 모델을 할 때(특히 딥러닝) 중요한 모델링 스킬에 대한
요약 정리
01. Underfitting과 Overfitting
- Underfitting : 모델이 너무 단순해서 데이터를 제대로 학습 못함
- Overfitting : 훈련 데이터를 너무 잘 학습해서 새로운 데이터에서 성능이 나오지 못하는 경우를 뜻함
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 1. 데이터 생성(노이즈 포함) 사인 함수
np.random.seed(0)
X = np.linspace(0, 1, 15) # 0과 1 사이 15개 데이터 입력
y_true = np.sin(2 * np.pi * X) # 정답함수 sin(2πx)
y = y_true + np.random.normal(0, 0.2, X.shape) # 노이즈 추가
X = X.reshape(-1, 1) # (15, 1) 형태로 reshape
# 2. 모델 복잡도를 다르게 해서 3가지 실험
degrees = [1, 3, 12] # underfit / 적절 / overfit
predictions = []
# 테스트용 데이터 (곡선을 그릴 용도)
X_test = np.linspace(0, 1, 100).reshape(-1, 1)
y_test_true = np.sin(2 * np.pi * X_test)
for d in degrees:
# 다항 특징 생성
poly = PolynomialFeatures(degree=d)
X_poly = poly.fit_transform(X)
X_test_poly = poly.transform(X_test)
# 선형 회귀 모델 학습
model = LinearRegression()
model.fit(X_poly, y)
# 예측값 저장
y_pred = model.predict(X_test_poly)
predictions.append((d, y_pred, model))
# 3. 시각화
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
for i, (d, y_pred, model) in enumerate(predictions):
axes[i].scatter(X, y, color='black', label='Training Data') # 훈련 데이터
axes[i].plot(X_test, y_test_true, label='True Function', linestyle='--') # 실제 함수
axes[i].plot(X_test, y_pred, label=f'Predicted (degree={d})') # 모델 예측
axes[i].set_title(f'Degree {d}\nMSE: {mean_squared_error(y_test_true, y_pred):.3f}')
axes[i].legend()
plt.tight_layout()
plt.show()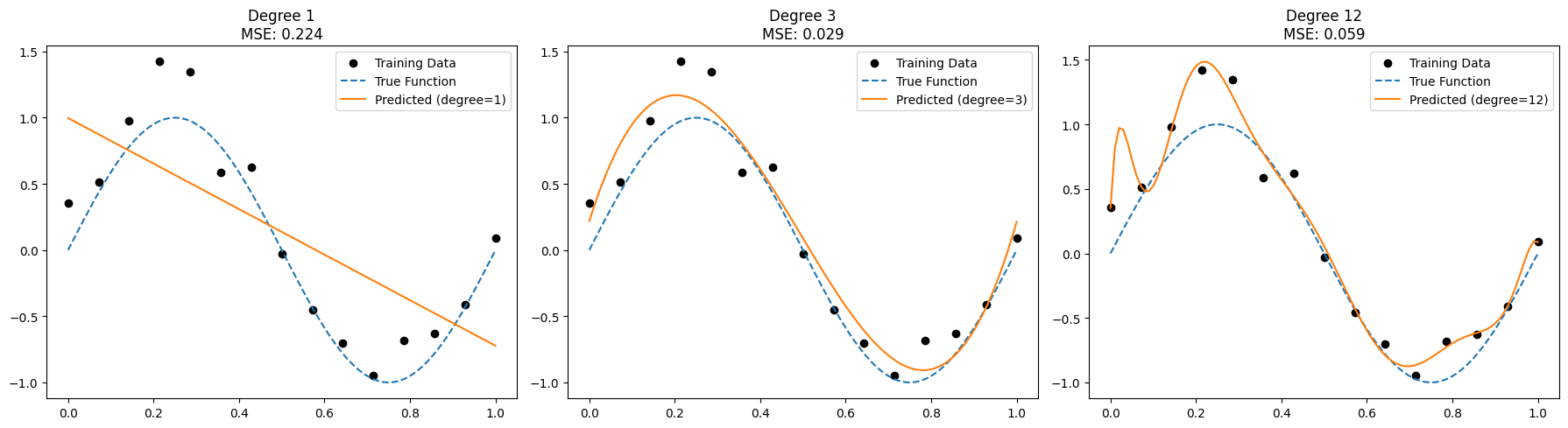
02. Bias-Variance Trade-off
- Bias : 모델이 정답과 멀리 떨어짐 (underfitting 경향)
- Variance : 훈련 데이터에 너무 민감 (overfitting 경향)
- Bias와 Variance는 구조적으로 동시에 줄이는 것이 불가능함. 그래서
둘 간에 상충(trade-off) 관계가 성립한다고 얘기함.
03. Regularization (정규화)
- 모델의 복잡도를 낮추어 overfitting 방지
- L2 기준으로는 아래와 같이 표현 가능
04. Early-stopping
- 검증 손실(val loss)이 더 이상 줄지 않을 때 학습을 조기 종료
- 과적합이 시작되기 전 모델 저장(일반화 성능 확보
- patience = 5 → 검증 손실이 5 epoch 동안 개선되지 않으면 stop
05. Batch Normalization (BN)
- 각 미니배치마다 입력 분포를 정규화 (평균 0, 분산 1)
- 내부 공변량 변화(Internal Covariate Shift) 완화
- 학습 안정화
- Dropout 없이도 일반화 성능 향상
06. 추가적인 스킬 소개
- Data Augmentation
- 입력 데이터 증강 (회전, 뒤집기 등), 데이터 부족 완화
- Weight Decay
- L2 regularization과 동일, 모델 축소화
- Ensemble
- 여러 모델 예측을 평균, 성능 향상, overfitting 완화
- Cross-Validation
- 여러 조합으로 평가, 안정적인 일반화 추정
