04-01) 기초 통계(1)

이번 노드에서는 외부 강사님 통해서 '기초 통계'를 배울 수 있었다.
외부 강사님께서는 학부는 공대 출신이고 석사 과정을 빅데이터 관련된
학교를 다니시다가 현업 경력이 좀 있으셨다.
나처럼 제조업, 금융업 경험보다는 IT쪽 이어서 많이 신선했다.
특히 외부 강사님께서 정말 수업자료를 열심히 준비해 오셨다.

01. 들어가기에 앞서

• 학교마다 커리큘럼은 다르겠지만 내가 다녔던 학교는 통계학 과목을
  통계학 입문, 통계 방법론 두 과목으로 나눠서 가르쳤다.
• 통계학 입문에서는 가설검정 앞부분까지 배웠던 것 같고, 통계 방법론은 통계학 입문 몇 주 복습하고 t분포, F분포, chi제곱 분포, anova, 회귀분석 등의 기본적인 방법론을 배웠다.
  • 통계학 입문에서도 베르누이분포, 이항분포, 포아송분포, 기하분포가 등장하고 정규분포, t분포 등에 대한 얘기도 나온다.
  • 통상 학부 수리통계학(1)이 통계학 입문 전반부 내용을 이론적으로 엄밀히(학부 레벨에서의 '엄밀함'이긴 하다.)다루고, 수리통계학(2)에서
    통계방법론에 해당하는 부분을 다루기는 한다.

02. 중심경향치와 산포도

• 실습 퀴즈 정답 위주로 정리하되, 더 좋은 얘가 있으면 배운 것과는
  다른 방식으로 접근해보고자 한다.

02-01) numpy 기술통계와 소수점 표현

import numpy as np
data = [10, 20, 20, 30, 40]

#코드작성
_mean = np.mean(data)
_median = np.median(data)
_var = np.var(data)
_std = np.std(data)

print(f'평균은 {_mean:.3f}')
print(f'중앙값은 {_median:.3f}')
print(f'분산은 {_var:.3f}')
print(f'표준편차는 {_std:.3f}')

02-02) 산술평균, 조화평균

• 수업 때는 '데이트 통장' 예시를 들었는데, 산술평균, 조화평균의
  기하학적 의미를 표현할 때는 더 좋은 예시가 있을 것 같았다.
• 가장 대표적으로는 속도, 거리를 통해 시간을 계산하는 경우다.
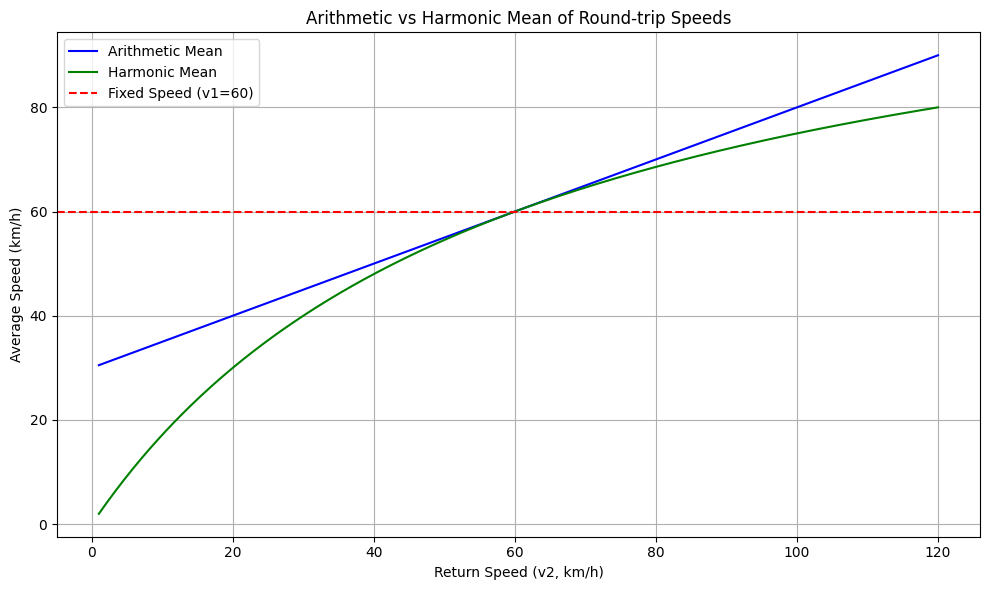
  • 예를 들어 A와 B지점의 거리가 120km고 A->B 일 때, 60km/h
    B<-A일 때, 20km/h로 이동한다고 생각해보자.
  • 그러면 평균 속도는 직관적으로는 40km/h일 것 같지만 그렇지가 않다.
  • 갈 때 2시간, 올 때 6시간 걸리니까 총 8시간 걸렸고 '왕복'이니까
    240km를 이동한거지. 그러니까 평균 속도는 30km/h가 된다.
  • 즉 2 x (갈 때 속도 x 올 때 속도)/(갈 때 속도 + 올 때 속도)
  • 2(60 x 20)/(60+20) = 30km/h

import numpy as np
import matplotlib.pyplot as plt

# 속도1 고정 (예: 갈 때 시속 60km/h)
v1 = 60
# 속도2 변화 (예: 돌아올 때 속도)
v2 = np.linspace(1, 120, 500)

# 산술평균
arith_mean = (v1 + v2) / 2

# 조화평균 (왕복 전체 평균 속력)
harm_mean = 2 * v1 * v2 / (v1 + v2)

plt.figure(figsize=(10, 6))
plt.plot(v2, arith_mean, label="Arithmetic Mean", color="blue")
plt.plot(v2, harm_mean, label="Harmonic Mean", color="green")
plt.axhline(v1, color="red", linestyle="--", label="Fixed Speed (v1=60)")

plt.xlabel("Return Speed (v2, km/h)")
plt.ylabel("Average Speed (km/h)")
plt.title("Arithmetic vs Harmonic Mean of Round-trip Speeds")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

02-03) 산포도: 표준편차와 변동계수

• 이건 수업 자료 때의 예시를 그대로 사용했다.
• 변동계수 = 표준편차/평균
• 향후 다르게 쓴 부분에 대해서는 명시를 할 생각이다.

# Numpy 방법
import numpy as np
com_a = [76300, 77400, 77900, 77200, 76900, 78800]
com_b = [6400, 7000, 7400, 6900, 7300, 7600]

# Numpy 방법

mean_a_np = np.mean(com_a)
std_a_np = np.std(com_a, ddof=1)
cv_a_np = std_a_np / mean_a_np

mean_b_np = np.mean(com_b)
std_b_np = np.std(com_b, ddof=1)
cv_b_np = std_b_np / mean_b_np

print(f'A회사의 변동계수 {cv_a_np:.3f}')
print(f'B회사의 변동계수 {cv_b_np:.3f}')

# Pandas 방법
import pandas as pd
data = pd.DataFrame({'Company A': com_a, 'Company B': com_b})
mean_a_pd = data['Company A'].mean()
std_a_pd = data['Company A'].std()
cv_a_pd = std_a_pd / mean_a_pd

mean_b_pd = data['Company B'].mean()
std_b_pd = data['Company B'].std()
cv_b_pd = std_b_pd / mean_b_pd

print(f'A회사의 변동계수 {cv_a_pd:.3f}')
print(f'B회사의 변동계수 {cv_b_pd:.3f}')

• boxplot도 그려보자

data = [10, 12, 23, 23, 16, 23, 21, 16, 7, 9]
#코드 작성
data_range = np.max(data) - np.min(data)
iqr = np.percentile(data,75) - np.percentile(data,25)

print(f'최대최소범위 {data_range:.3f}')
print(f'iqr {iqr:.3f}')

import matplotlib.pyplot as plt
plt.boxplot(data)
plt.show()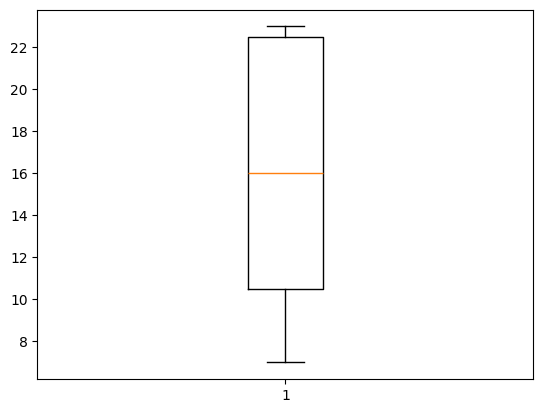

03. 데이터 시각화

• seaborn 패키지에 내장된 tips데이터 활용

03-01) 통계 분석 실습

• print가 아니라 display 명령어 쓴 부분이 재미있었음.
• print명령어 보다 더 깔끔하다는 느낌을 받았음.

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
tips = sns.load_datasets('tips')
display(tips.head(3))
display(tips.describe(include = 'all'))

• total_bill의 기본 통계량(평균, 중앙값, 분산, 표준편차)을 계산

mean = tips['total_bill'].mean()
median = tips['total_bill'].median()
variance = tips['total_bill'].var()
std_dev = tips['total_bill'].std()
print(f"Mean: {mean:.3f}, Median: {median:.3f}, Variance: {variance:.3f}, Std Dev: {std_dev:.3f}")

• 요일별 팁의 평균 비교 문제: 요일(day)별 팁(tip)의 평균을 계산하고, 가장 팁이 많이 주어진 요일을 구하시오.

tips.groupby("day")["tip"].mean().round(3)

• 흡연자와 비흡연자(smoker)의 total_bill 평균과 표준편차를 비교

tips.groupby("smoker")["total_bill"].agg(["mean","std"])

• 성별(sex)과 흡연 여부(smoker)에 따라 평균 팁이 어떻게 달라지는지 확인

tips.groupby(["sex", "smoker"])["tip"].mean()

• 요일별 총 total_bill의 합계를 계산하고, 어떤 요일에 가장 많은 매출이 발생했는지 확인

tips.groupby("day")["total_bill"].sum()

03-02) 시각화

• countplot

# countplot: x축 범주형, y축 관측치
sns.countplot(data = tips, x = 'day')

• barplot

# barplot: X축이 범주형, Y축이 연속형 값
sns.barplot(data = tips, x = 'sex', y = 'tip', estimator = 'mean')

• boxplot

sns.boxplot(data = tips, x = 'time',y = 'total_bill')

• histplot

sns.histplot(data = tips, x = 'total_bill')

• scatterplot

sns.scatterplot(data = tips, x = 'total_bill', y = 'tip')

• 상관계수 보기

sns.pairplot(data = tips)

04. numpy.random()

• numpy.random() 연습해보기

04-01) 균등분포 난수 생성

# 난수 생성
data = np.random.rand(100)
# 평균과 표준편차 계산
mean = np.mean(data)
std_dev = np.std(data)

print(f"Mean: {mean:.3f}")
print(f"Standard Deviation: {std_dev:.3f}")

04-02) 주사위 문제

• 주사위를 100번 던졌을때 나올 숫자를 시뮬레이션하고 각 숫자가
  나온 횟수를 계산

import numpy as np
import matplotlib.pyplot as plt

# 1. 주사위 던지기 시뮬레이션
rolls = []
for _ in range(100):  # 주사위를 100번 던짐
    roll = np.random.randint(1, 7)  # 1부터 6까지의 정수 중 하나를 무작위로 선택
    rolls.append(roll)

# 2. 각 숫자의 빈도 계산
roll_counts = {}
for number in range(1, 7):  # 주사위는 1부터 6까지의 숫자를 가짐
    roll_counts[number] = rolls.count(number)  # 각 숫자가 rolls에 몇 번 등장했는지 계산

# 3. 결과 출력
print("Dice roll counts:", roll_counts)

# 4. 히스토그램 그리기
plt.hist(rolls, bins=np.arange(1, 8) - 0.5, color='skyblue', edgecolor='black')
plt.title("Dice Roll Simulation (100 Rolls)")
plt.xlabel("Dice Number")
plt.ylabel("Frequency")
plt.yticks(range(0, 26,2))
plt.xticks(range(1, 7))  # X축에 1부터 6까지 숫자를 표시
plt.show()

04-03) 정규분포 데이터 생성

• 평균 50, 표준편차 10인 정규분포에서 1,000개의 데이터를 생성하고
  히스토그램 그리기

import matplotlib.pyplot as plt

# 정규분포 데이터 생성
data = np.random.normal(loc=50, scale=10, size=1000)

# 히스토그램 그리기
plt.hist(data, bins=30, color='blue', alpha=0.7)
plt.title("Histogram of Normal Distribution")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()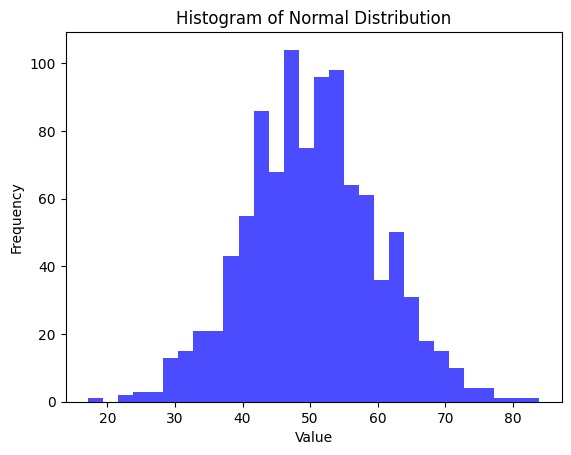

04-04) 로또 생성기

• 강사님 code가 당연히 내 것보다 훨씬 훌륭하지만 '로또를 사는 입장'
  에서는(물론 난 잘 안 산다. 정확하게 기억은 안 나는데 로또를 살 때
  기대값이 -4,700원쯤 되거든.) '보너스 번호'를 맞출 필요가 없다.
• 그래서 다소 조악하지만 내 코드를 올려둔다.
  • 5,000원치 살 때를 기준으로 삼았다.

import numpy as np

num_trial = 5 # 5,000원치 기준 (10,000원이면 10을 입력)
result = []

for i in range(1, num_trial+1):
    num_list = np.arange(1,46)
    chosen_num = np.random.choice(num_list,6,replace=False)
    chosen_num.sort()
    result.append(chosen_num)

for i in lotto in enumerate(result, i):
    print(f"{i}번째 로또번호 {result}")

• 그러면 결과는 이렇게 나온다.
  

• 사실 기초 확률을 배웠으면 다들 알 것이다. 로또 1등 당첨 확률은
  800만 분의 1 정도 된다는 것을.

  • 좋아하는 번호를 넣나, 1~6을 그냥 넣나, 난수 추출해서 넣나
    당첨될 확률은 같다.
  • 그럼에도 당첨되는 사람들이 매주 나오는게 신기하긴 하다.
  • 사실 신기할 것은 없는게 한 게임에 1000원이고 로또 판매액이
    매주 1000억이라 가정하면 1억 게임 산거잖아? 그러면 매주 10명쯤
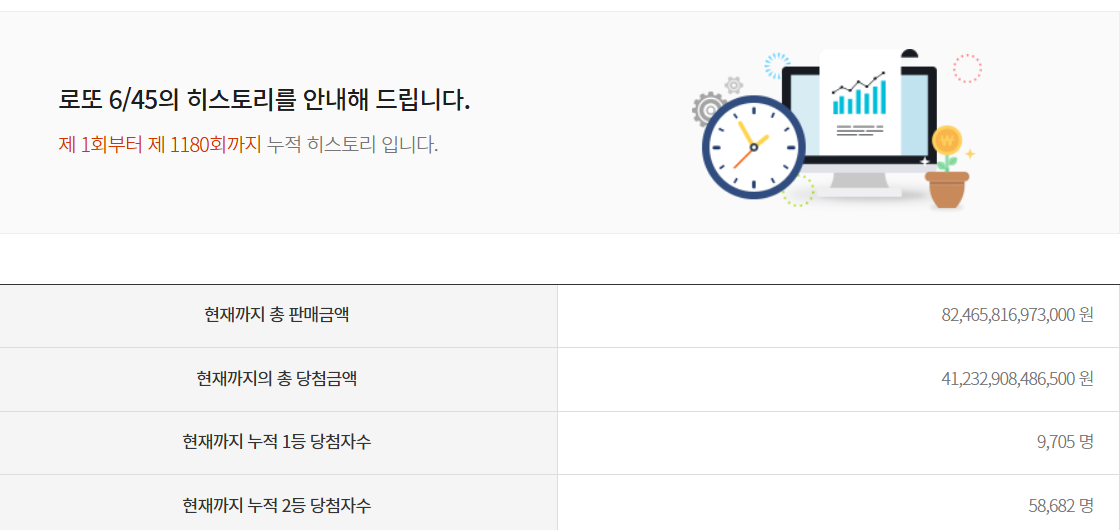
    당첨자가 나와도 이상할 것은 없지.
  • 로또 1180회면 대충 20년 정도 한거지. 20년간 1,2등 다 합쳐도
    7만명이 안된다.(인생 살면서 수십 만 분의 1 이하로 운이 좋거나
    나쁜 적이 있었는지 떠올려보면 확률적으로 말이 안되지.)
  • 로또 사시는 분들도 '될 거라는 기대'보다는 '재미'로 하는거지.
    

• GPT에게 좀 물어봤다. 50년간 매주 1만(10게임) 살 때, 당첨금의
  기대값이 어떨지.
  

• GPT에게 이런 것도 물어봤다. 매주 1만원씩 50년간 꾸준히 미국
  배당주에 투자할 때(보수적으로 수익률 5-6% 잡아보자.),
  어떻게 자산이 변하는지.(리얼티인컴 사면 연배당률 5.5%는 넘으니까,
  S&P 500은 배당은 적더라도 연 평균 상승률이 7%쯤 되니까.)

import numpy as np

# 설정
weekly_investment = 10000  # 매주 1만원
years = 50
weeks_per_year = 52
total_weeks = years * weeks_per_year

# 연 수익률 가정
dividend_stock_return = 0.055  # 5.5%
sp500_return = 0.07            # 7%

# 적립식 투자 계산 함수
def future_value_regular_investment(weekly_amount, weeks, annual_return):
    r = (1 + annual_return) ** (1 / 52) - 1  # 주간 수익률
    return weekly_amount * (((1 + r) ** weeks - 1) / r)

# 계산
fv_dividend = future_value_regular_investment(weekly_investment, total_weeks, dividend_stock_return)
fv_sp500 = future_value_regular_investment(weekly_investment, total_weeks, sp500_return)

fv_dividend, fv_sp500

• 계산 결과가 많이 충격적이었다.
  • 5.5% 수익률 가정하면 약 1억 3천만원 정도 되고, 7% 수익률
    가정하면 2억 1800만원 정도 된다.
  • 결국 매주 1-2만원씩 미국 배당주에 꾸준히 투자하는게 로또보다
    훨씬 낫다는 얘기지.
• 이게 흔히 경영학 재무 분야(재무관리, 기업재무, 투자론)나 경제학의
  화폐금융론에서 아주 기초적으로 다루는 '복리의 힘'인 것 같다.
  • 어떤 종류의 학력, 커리어, 연봉을 가지고 살더라도 자신의 위치에서
    '작은 노력'이라도 '꾸준히' 이어갈 수 있다면, 긴 시간이 지났을 때
    인생에 있어서 큰 힘이 되지 않을까 하는 생각이 문득 들었다.

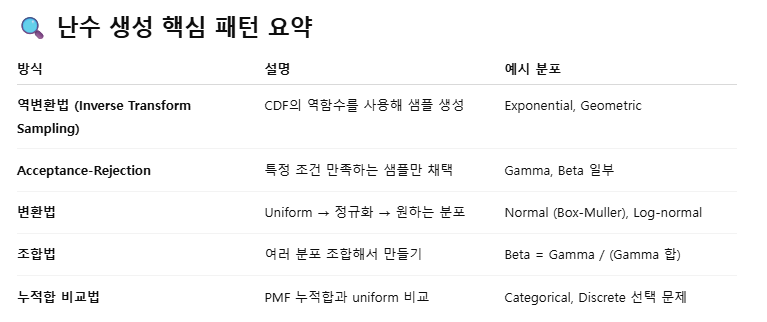
05. 참고 사항

• 당연히 '모두의 연구소' 뿐만 아니라 모든 종류의 데이터 분석가,
  데이터 사이언티스트 KDT 프로그램에서는 보통 저 '난수'가 어떻게
  만들어지는지 원리를 다루지는 않는다.
• 나도 매우 오래 전에 배운 거라서(전산통계학 배울 때, matlab이었음),
  일단 gemini/gpt 힘을 빌려서 간단하게 내용을 남겨두고자 한다.
• 주요 분포별 난수 생성 방법

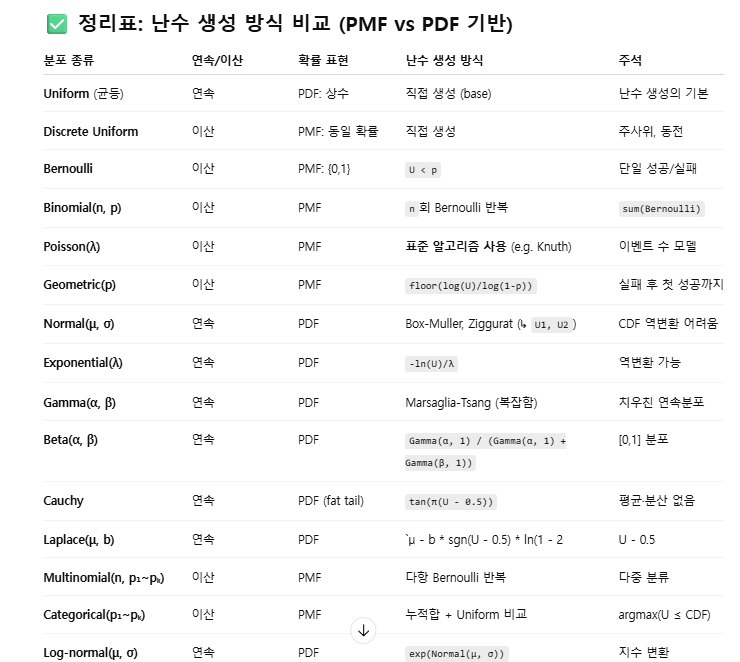
• 사실 이런 내용은 KDT 6개월 짜리 뿐만 아니라, 재직자용 '단기 심화'
  KDT 과정에서도(아니면 여타 부트캠프에서도 잘 안 다룰 것 같다.)
  • 카카오나 여타 주요 기업들이 코딩 테스트 쳐서 선발하는 캠프는
    어떨지 궁금하긴 하다. 너무 이론적이라 안 다룰 듯.