04-03) 기초통계(3)

사실 강사님께서 정말 열심히 준비하셨고, 2-3주차 때의 AARRR Framework도 복습할 수 있어서 뜻깊은 모듈이긴 했는데, 사실 이 때
강사님께서 만든 '중심극한정리' 예시가 살짝 아쉬웠다.

01. 중심극한정리(Central Limit Theorem) 수업 예시

• 수업 시간 때의 첫 예시는 균등 분포, 이항 분포, 정규 분포의 '반복수'가 1000번인 경우에 해당한다. 표본의 크기와는 상관이 없다.
  

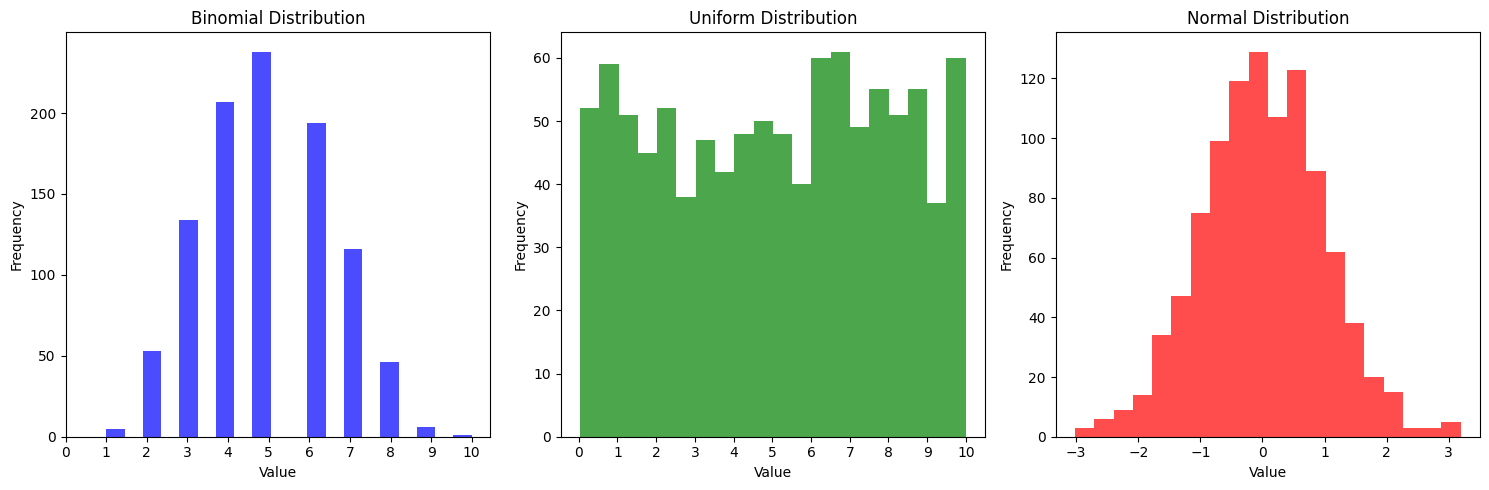
• 균등 분포, 이항 분포, 정규 분포에서 30개씩 표본을 뽑고 평균을
  구한 다음, 반복수를 500번으로 설정(이게 CLT예시)
  

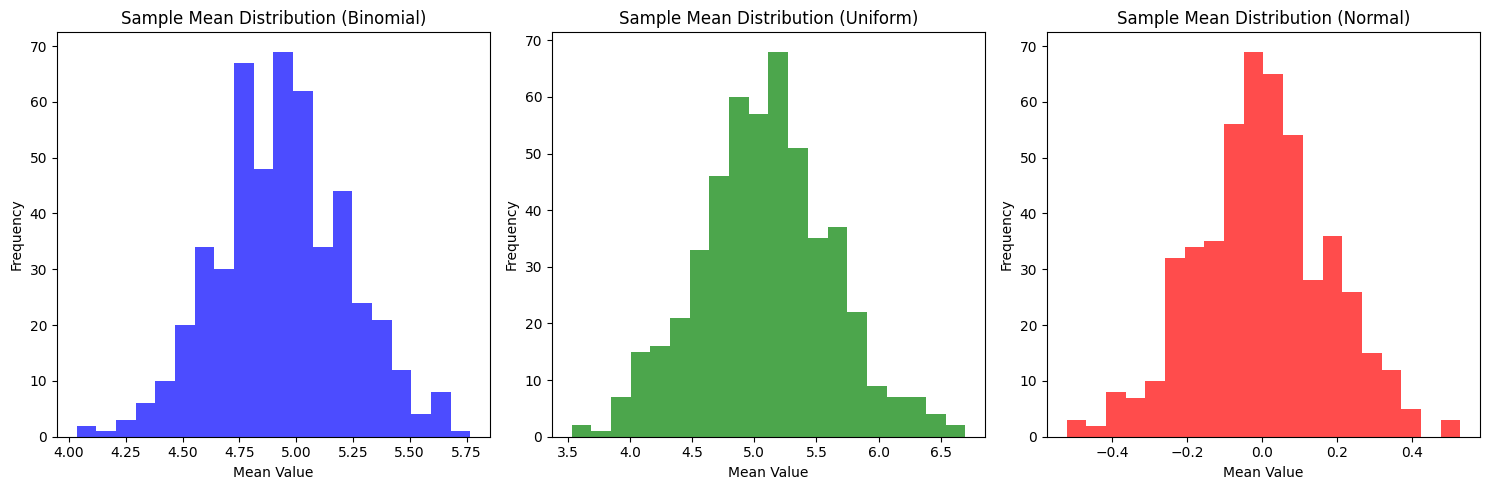
• 물론 이렇게 해도 되긴 한다. 위의 이항분포(파란색)와 아래의 이항분포를 비교하면 되니까.

02. 중심극한정리 - 다른 예시

• 중심극한 정의는 유한한 분산이 정의된 확률공간에서 표본 평균의
  평균이 정규분포에 분포 수렴한다.(이 때는 iid 가정을 한다.)
  이런 의미거든. 사실 중심극한정리도 여러 종류가 있다. IID 가정을
  고수하지 않아도 되는 Lyapunov의 중심극한정리도 있으니까.
• 본론으로 돌아와서, 다른 예시를 들어본다면 '표본의 크기'가 3, 5, 10, 15, 20, 30으로 커지면서 '표본의 평균'이 (반복수가 500, 1000이든)
  정규분포에 근사하는 예시를 보여주었으면 어떠셨을까 하는 아쉬움이
  조금 들었다.
• 관련 코드

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform

np.random.seed(42)

sample_sizes = [3, 5, 10, 15, 20, 30]
num_samples = 500
true_dist = uniform(loc=0, scale=10)

plt.figure(figsize=(15, 8))

for i, n in enumerate(sample_sizes):
    sample_means = []
    for _ in range(num_samples):
        sample = true_dist.rvs(size=n)
        sample_mean = np.mean(sample)
        sample_means.append(sample_mean)
    
    plt.subplot(2, 3, i+1)
    plt.hist(sample_means, bins=30, color="skyblue", edgecolor="black", alpha=0.7, density=True)
    plt.title(f"Uniform Dist. Sample Means (n={n})")
    plt.xlabel("Sample Mean")
    plt.ylabel("Density")

plt.tight_layout()
plt.show()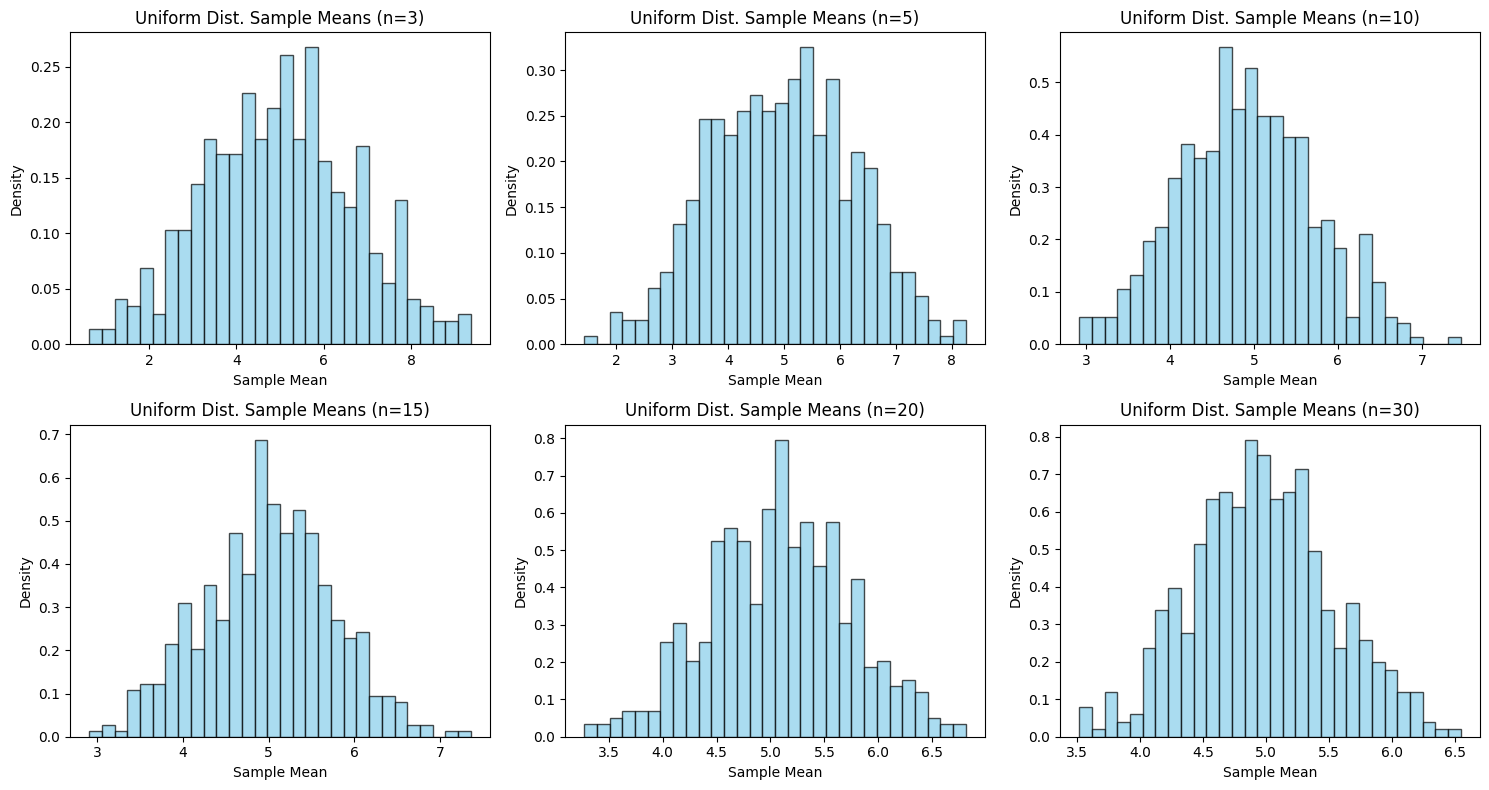

• 그런데 균등 분포(Uniform distribution)는 좌나 우로 치우치지 않은
  분포여서 표본의 크기가 증가(3,5,10,15,20,30) 하는 효과가 극명해
  보이지는 않았다.
• 그러면 '한쪽으로 치우친' 지수분포를 예로 들어보면 어떨까?
• 반복수는 1000에서 500으로 줄였다.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon  # 

np.random.seed(42)

sample_sizes = [3, 5, 10, 15, 20, 30]
num_samples = 500
true_dist = expon(scale=1)  # 평균=1, 분산=1 (scale=1/λ)

plt.figure(figsize=(15, 8))

for i, n in enumerate(sample_sizes):
    sample_means = []
    for _ in range(num_samples):
        sample = true_dist.rvs(size=n)
        sample_mean = np.mean(sample)
        sample_means.append(sample_mean)
    
    plt.subplot(2, 3, i+1)
    plt.hist(sample_means, bins=30, color="tomato", edgecolor="black", alpha=0.7, density=True)
    plt.title(f"Exponential Dist. Sample Means (n={n})")
    plt.xlabel("Sample Mean")
    plt.ylabel("Density")

plt.tight_layout()
plt.show()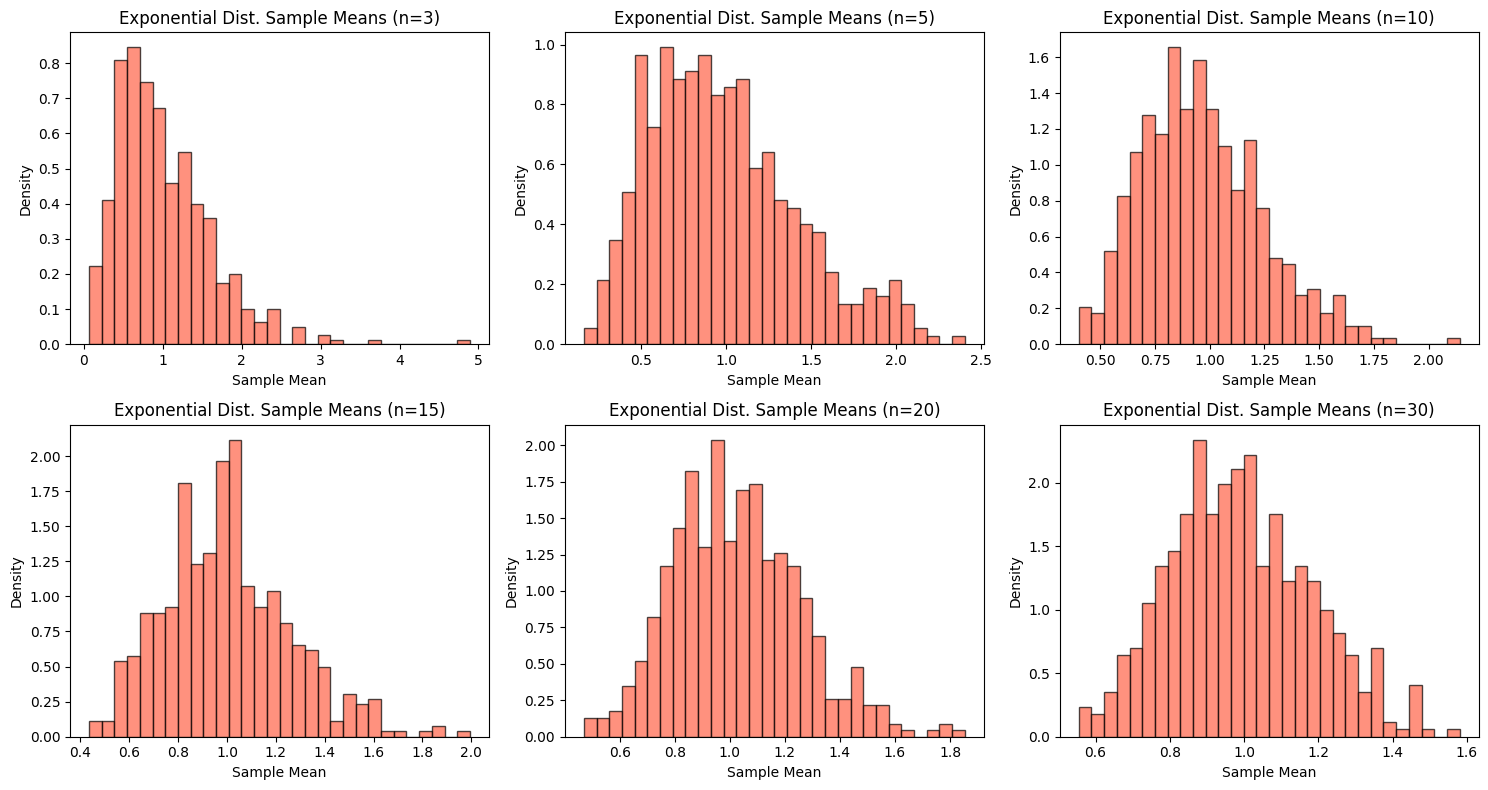

03. 그 외에 다룬 내용들

• Z검정
• t검정(독립이표본 t검정)
  • 서로 독립된 두 집단 간의 평균 비교
• AB test
  • 신규 페이지에 따른 전환율이 유의미한 변화가 있는지 측정