[밑바닥부터 시작하는 딥러닝] 2장 퍼셉트론

밑바닥부터 시작하는 딥러닝 깃허브: https://github.com/WegraLee/deep-learning-from-scratch

---

퍼셉트론

퍼셉트론은 신경망(딥러닝)의 기원이 되는 알고리즘으로 다수의 신호를 입력 받아 하나의 신호를 출력한다.

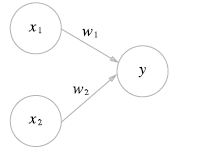
위 그림은 입력으로 2개의 신호를 받는 퍼셉트론의 예이다. $x_1$과 $x_2$는 입력 신호, $y$는 출력 신호, $w_1$과 $w_2$는 가중치를 뜻한다. 위 그림의 원을 뉴런 혹은 노드라고 불른다. 입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치($w_1x_1$, $w_2x_2$)가 곱해진다. 뉴런에서 보내온 신호의 총합이 정해진 한계를 넘어설 때만 1을 출력한다. 그 한계를 임계값이라고 하며, $\theta$로 나타낸다.

퍼셉트론의 동작을 식으로 나타내면 다음과 같다.

$\theta$ 대신 편향 $b$를 적용하면 다음과 같다.

여기서 가중치 $w_1$, $w_2$는 각 입력 신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수이고, 편향 $b$는 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조정하는 매개변수이다.

단순한 논리 회로 구현

AND 게이트

$x_1$	$x_2$	$y$
0	0	0
0	1	0
1	0	0
1	1	1

이를 만족하는 ($w_1$, $w_2$, $\theta(b)$)의 값은 무수히 많다. (0.5, 0.5, 0.7(-0.7)), (0.5, 0.5, 0.8(-0.8)) ... 등등 모두 AND 게이트의 조건을 만족한다.

편향 $b$를 사용하여 간단하게 구현하면 다음과 같다.

def AND(x1, x2):
	x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
    	return 0
    else:
    	return 1

NAND 게이트

$x_1$	$x_2$	$y$
0	0	1
0	1	1
1	0	1
1	1	0

NAND 게이트를 만족하는 값도 무수히 많다. AND 게이트 매개변수의 부호를 모두 반전하면 NAND 게이트를 만족한다. (-0.5, -0.5, -0.7(0.7)) ...

def NAND(x1, x2):
	x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
    	return 0
    else:
    	return 1

OR 게이트

$x_1$	$x_2$	$y$
0	0	0
0	1	1
1	0	1
1	1	1

def OR(x1, x2):
	x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
    	return 0
    else:
    	return 1

한계

논리 회로 중 XOR 게이트는 퍼셉트론으로 구현이 안된다.

OR 게이트를 만족시키는 ($b, w_1, w_2$) 값 (-0.5, 1.0, 1.0)을 퍼셉트론 식에 대입하여 좌표 평면에 그래프로 나타내면 다음과 같다.

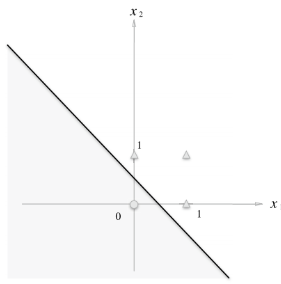
위에서 구현한 세 가지의 논리 회로는 위 그림과 같이 선형적으로 놔눠진다.

하지만 XOR 게이트는 다음 그림과 같이 비선형적으로 나눠져야 한다.

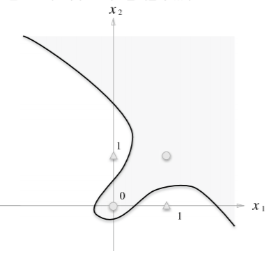
단층 퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있기 때문에 한계가 있다.

다층 퍼셉트론

다층 퍼셉트론은 여러개의 퍼셉트론을 층으로 쌓아 만든다.

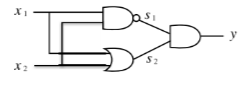
XOR 게이트는 기존 세 개의 게이트를 조합해 만들 수 있다.

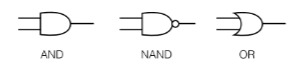
$x_1$	$x_2$	$s_1$	$s_2$	y
0	0	1	0	0
1	0	1	1	1
0	1	1	1	1
1	1	0	1	0

XOR 게이트는 기존 세 개의 게이트를 구현한 함수를 이용해 구현할 수 있다.

def XOR(x1, x2):
	s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    retunr y

뉴런을 이용한 퍼셉트론으로 표현하면 다음과 같다.

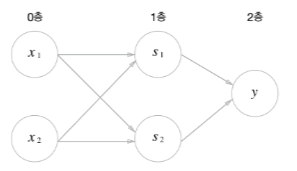
이처럼 다층 퍼셉트론은 단층 퍼셉트론으로는 표현하지 못하는 것을 구현할 수 있다.