https://www.youtube.com/watch?v=061eXyAFRuI&list=PLFgS-xIWwNVX-zm4m6suWC9d7Ua9z7fuT&index=33

📌 벨만포드

• 그래프에서 최단 거리를 구하는 알고리즘

기능	특징	시간 복잡도(노드수 : V , 에지 수 : E)
특정 출발 노드에서 다른 모든 노드까지의 최단 경로 탐색	- 음수 가중치 에지도 수행 가능 - 전체 그래프에서 음수 사이클의 존재 여부 판단 가능	O(VE)

◾ 벨만포드 알고리즘의 원리

1. 에지 리스트로 그래프를 구현하고 최단 경로 리스트 초기화

• 에지를 중심으로 동작하므로 그래프를 에지 리스트로 구현
• 최단 경로 리스트를 출발노드는 0, 나머지는 무한대로 초기화

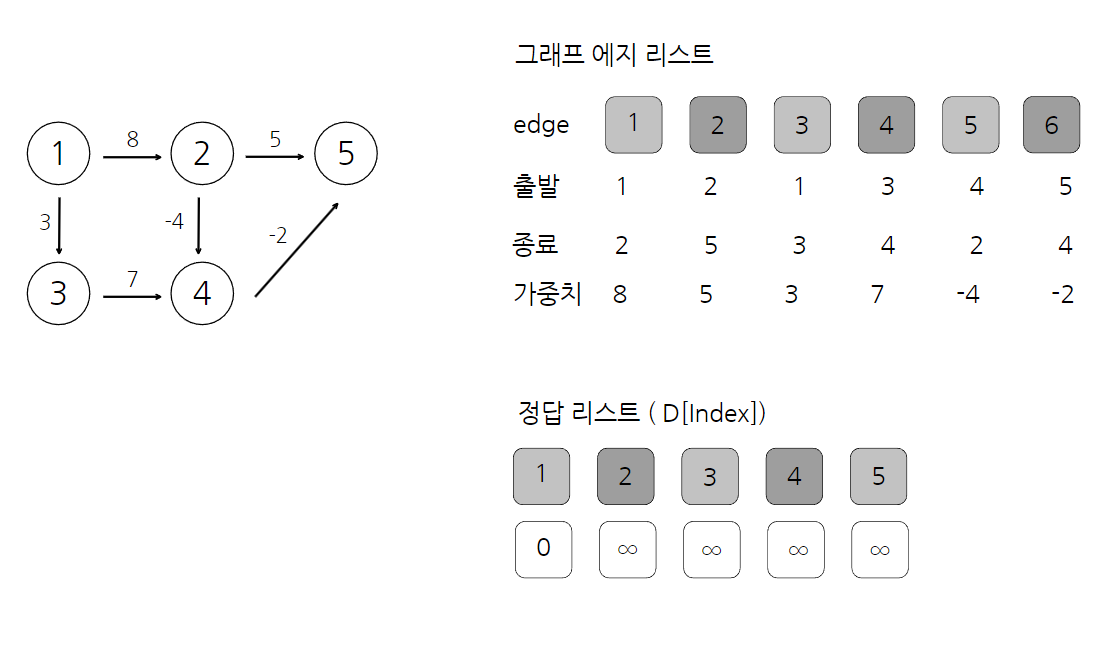
2. 모든 에지를 확인해 정답 리스트 업데이트하기

• 최단 거리 리스트에서 업데이트 반복 횟수는 노드 개수 n-1
  → 노드 수가 N개이고 음수 사이클이 없을 때 두 노드의 최단 거리를 구성 할 수 있는 최대 개수는 N-1 이기 때문
• 모든 에지 E = ( s, e, w)에서 다음 조건을 만족하면 업데이트 실행
  → 업데이트 반복 횟수가 K번이라면 해당 시점에 정답 리스트 값은 시작점에서 K개의 에지를 사용 했을 때 각 노드에 대한 최단 거리
• 음수 사이클이 없을 때 N-1 에지 사용 횟수를 반복하면 출발 노드와 모든 노드간의 최단 거리를 알려주는 정답 리스트가 완성

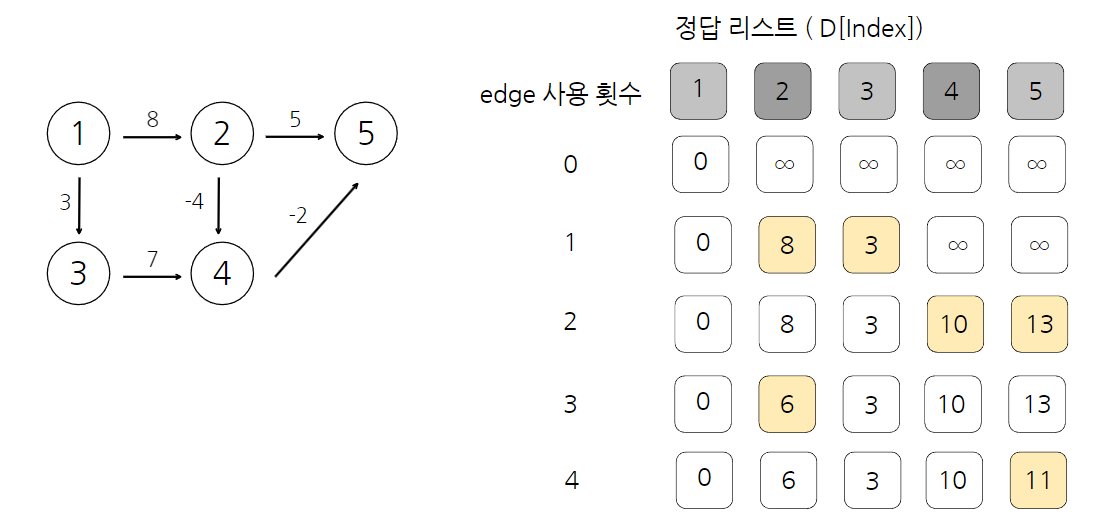
• 1개의 에지를 사용 했을 때 시작점에서 다른 노드까지 최단거리

🔶 업데이트 조건과 방법

D[s] != ∞ 이며 D[e] > D[s] + w일 때 D[e] = D[s] +w로 리스트의 값 업데이트
→ 시작이 무한대가 아니고 (계산 불가), 종료하는 곳에 들어 있는 최단 거리 리스트의 값보다 시작 점에 있는 최단 거리의 값 + 가중치가 더 작으면 (새롭게 들어오는 값이 더 작으면) 노드의 값을 새로운 값으로 업데이트

• 음수 사이클이 없을 때 최대 에지 개수가 나오려면 사향 트리 형태에서 양 도착 노드를 선택해야함

• 에지의 출발노드를 s, 종료 노드를 e 에지 가중치를 w로 가정

  
  

3. 음수 사이클 유무 확인하기

• 음수 사이클 유무를 확인하기 위해 모든 에지를 한 번씩 다시 사용해 업데이트 되는 노드가 발생하는지 확인
  → 만약 업데이트 되는 노드가 있다면 음수 사이클이 있다는 뜻이고 2단계에서 도출한 정답 리스트가 무의미하고 최단 거리를 찾을 수 없는 그래프라는 뜻이 됨
• 음수 사이클이 존재하면 이 사이클을 무한하게 돌수록 가중치가 계속 감소하므로 거리를 구할 수 없음

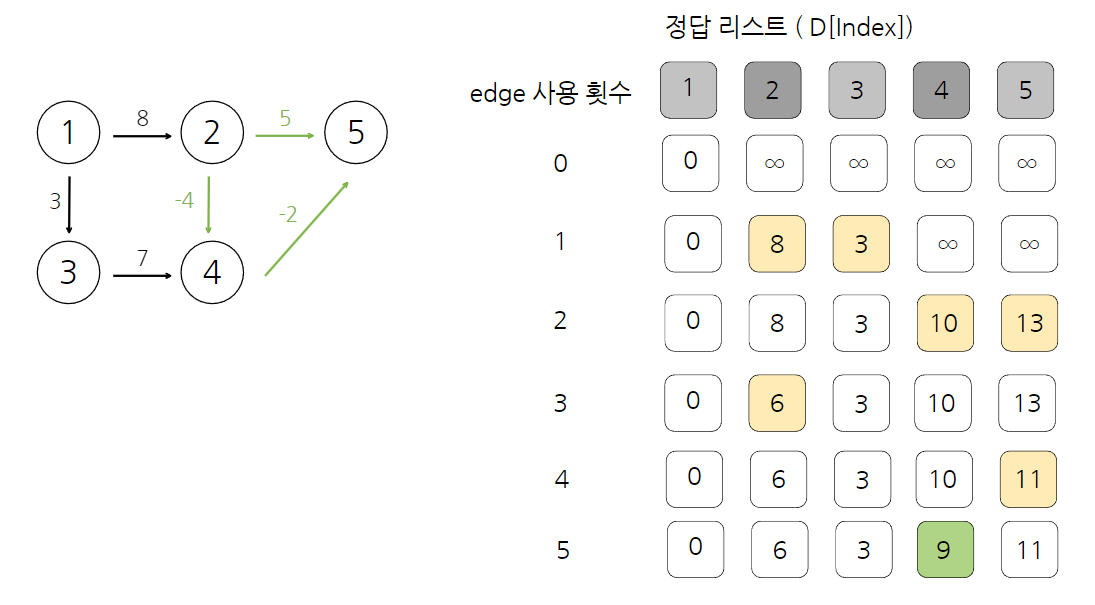
• 음수 사이클 체크를 위해 에지를 한 번 더 반복 함.
• 5번째에서도 리스트 갱신 (index = 4)이 일어났으므로 음수 사이클이 그래프에 존재
  즉, 에지를 한 번 더 반복 시 업데이트 되면 최단거리가 아니므로 음수 사이클이 존재