https://www.youtube.com/watch?v=1d9sqmuLy-o&list=PLFgS-xIWwNVX-zm4m6suWC9d7Ua9z7fuT&index=37
📌 세그먼트트리
- 주어진 데이터의 구간 합 데이터 업데이트를 빠르게 수행하기 위해 고안해낸 자료구조의 형태
- 더 큰 범위는 인덱스 트리라고 불림
◾ 세그먼트 트리의 핵심이론
- 종류 : 구간합, 최대/최소 구하기
- 구현 단계 : 트리 초기화하기, 질의값 구하기(구간합 또는 최대/최소), 데이터 업데이트하기
1. 트리 초기화하기
- 리프 노드의 개수가 데이터의 개수(N)이상이 되도록 트리 배열을 만든다
- 트리 배열의 크기를 구하는 방법
2^k >= N을 만족하는 K값을 구한 후2^k * 2를 트리 배열의 크기로 지정
ex) 샘플데이터가 {5, 8, 4, 3, 7, 2, 1, 6} 인경우 N=8이므로 2³ >=8 이므로 배열의 크기를 2³ * 2 = 16으로 정의
- 리프 노드에 원본 데이터를 입력. 이 때 리프 노드의 시작 위치를 트리 배열의 인덱스로 구해야 하는데 구하는 방식은
2^k를 시작 인덱스로 취한다.
예를들어 K값이 3이면 start index = 8

- 리프노드를 제외한 나머지 노드 값을 채움 (
2^k -1부터 1번쪽으로 채움) - 채워야 하는 인덱스가 N이라고 가정하면 자신의 자식 노드를 이용해 해당 값을 채울 수 있음
- 자식 노드의 인덱스는 이진 트리 형식이기 때문에
2N,2N+1이 됨

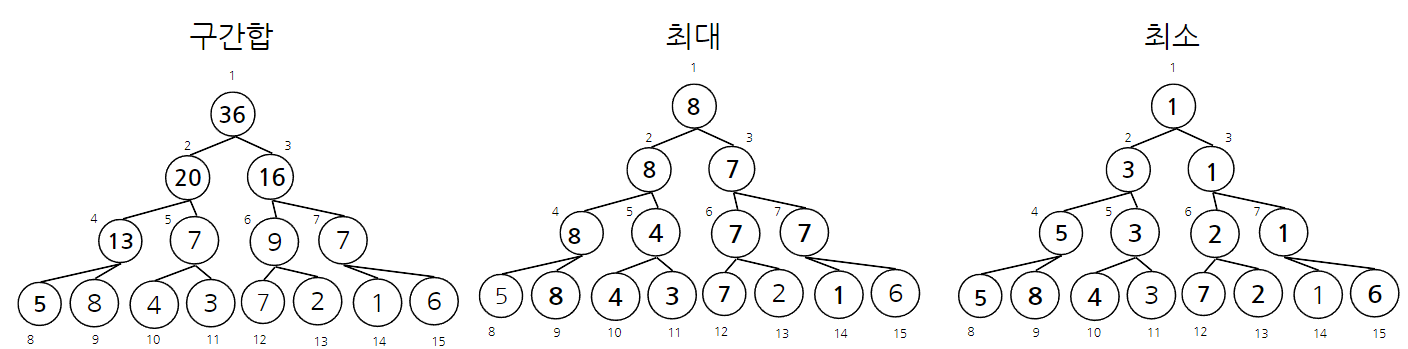
- 위 3개의 세그먼트 트리를 구조화하면 아래와 같이 됨
- 세그먼트 트리를 구성 해 놓으면 이후 질의와 관련된 결과값이나 데이터 업데이트 요구사항에 관해 좀 더 빠른 시간 복잡도 안에서 해결 가능
2 질의값 구하기
- 주어진 질의 인덱스를 세그먼트 트리의 리프노드에 해당하는 인덱스로 변경
- 기존 샘플을 기준으로 한 인덱스값과 세그먼트 트리계열에서의 인덱스 값이 다르기 때문에 인덱스를 변경해야함
🔶 인덱스 변경 방법
세그먼트 트리 index = 주어진 질의 index + 2^K - 1
🔶 질의값 구하는 과정
- start_index % 2 == 1일때 노드를 선택
- end_index % 2 == 0일때 노드를 선택
- start_index depth 변경 : start_index = (start_index+1)/2 연산 수행
- end_index depth 변경 : end_index = (end_index -1)/2 연산 수행
- 1~4 반복하다가 end_index < start_index가 되면 종료
- 1~2에서 해당 노드를 선택 했다는 것은 해당 노드의 부모가 나타내는 범위가 질의 범위를 넘어가기 때문에 해당 노드를 질의값에 영향을 미치는 독립 노드로 선택하고 해당 노드의 부모 노드는 대상 범위에서 제외한다는 뜻
- 부모 노드를 대상 범위에서 제거하는 방법은 3~4에서 질의 범위에 해당하는 부모 노드로 이동하기 위해 인덱스 연산을
(index+1)/2,(index-1)/2로 수행 - 질의에 해당하는 노드를 선택하는 방법은 모두 동일하며 선택된 노드들에 관해 마지막 연산 방식만 다름
🔶 질의에 해당하는 노드 선택 방법
- 구간합 : 선택된 모두 더함
- 최댓값 : 선택된 노드 중 max값 선택해 출력
- 최솟값 : 선택된 노드 중 min값 선택해 출력
- 리프 노드의 인덱스로 변경
start_index = 2+7=9
end_index = 6+7=13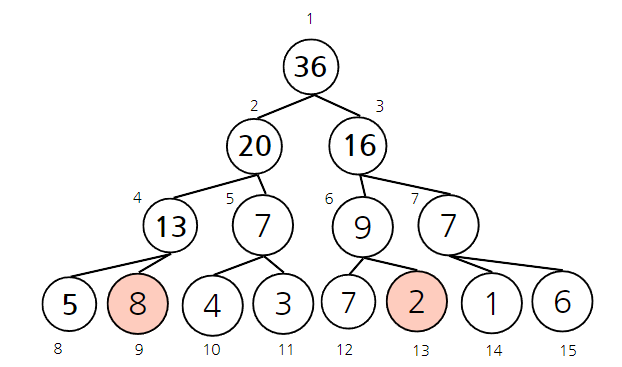
- 부모 노드로 이동
start_index %2 = 9 % 2 = 1 //노드 선택
// 1이 나왔다는 것은 인덱스가 오른쪽을 뜻함
// 오른쪽인 경우 부모 노드를 사용하면 안됨 => 해당 부모 노드의 왼쪽도 가지고 있기 때문에 미선택
// 독립노드로 선택 해 놓음 (8)
// 이미 해당 노드의 부모 노드는 사용하면 안되기 때문에 옆 부모 노드로 가야함
// 8의 부모노드인 13이 아닌 7을 선택
end_index %2 = 13 % 2 = 1 // 노드 미선택
// 해당 노드를 품고있는 부모 노드가 있기 때문에 해당 노드를 선택하지않고 부모 노드로 뛰어 올라감
start_index = (start_index +1) /2 = 10 /2 = 5
// +1을 하는 이유는 독립 노드로 선택되어 8의 부모 노드인 13이 아닌 7을 선택해야 하기 때문에
end_index = (end_index -1) /2 = 12/2 =6
// 독립 노드로 선택되지 않았기 때문에
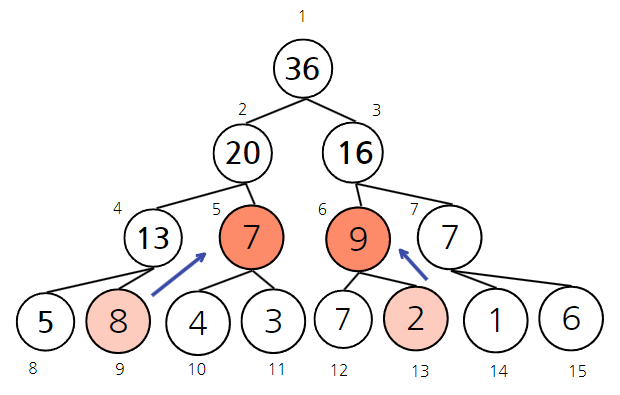
- 한 번 더 부모 노드로 이동
start_index %2 = 5%2 = 1 // 노드 선택
end_index %2 = 6%2 = 0 // 노드 선택
start_index = (start_index +1) /2 = 6/2 = 3
end_index = (end_index -1) /2 = 5/2 =2
//end_index <start_index이므로 종료

선택된 7, 9, 8 을 더하면 [9] ~ [13]의 구간 합이 나온다.
- 업데이트 하기
-
어떤 값을 업데이트 할 것인지에 관해서는 트리 타입별로 다르다
→ 부모 노드로 이동하는 방식은 세그먼트 트리가 이진 트리이므로index = index = index/2로 변경 -
구간합 : 원래 데이터와 변경 데이터의 차이만큼 부모 노드로 올라가면서 변경
-
최댓값 : 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교하면서 더 큰 값으로 업데이트, 업데이트가 일어나지 않으면 종료
-
최솟값 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교하면서 더 작은 값 으로 업데이트, 업데이트가 일어나지 않으면 종료
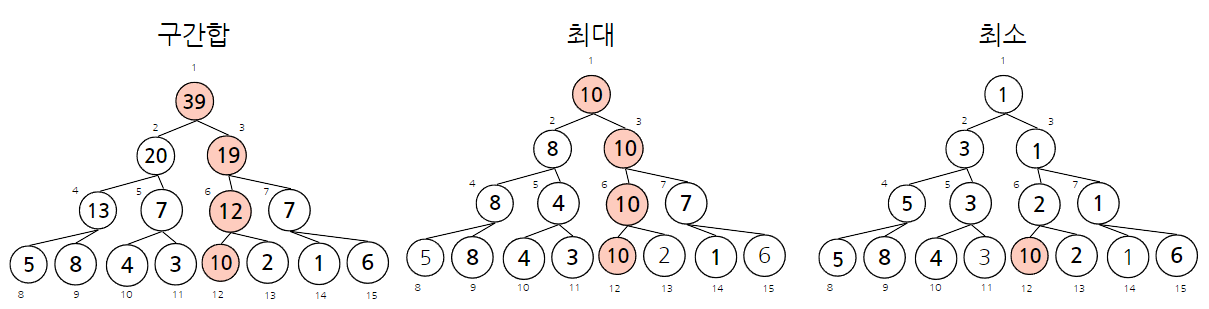
- 최소값에서 10과 2 비교 후 부모노드의 값이 업데이트 되지 않았기 때문에 종료

