https://www.youtube.com/watch?v=U22u6E2udUI&list=PLFgS-xIWwNVX-zm4m6suWC9d7Ua9z7fuT&index=41

📌 조합

• 조합은 nCr로 표현하고 이는 n개의 숫자에서 r개를 뽑는 경우의 수를 뜻함
• 조합과 비교되는 순열은 nPr로 표현되고 n개의 숫자 중 r개를 뽑아 순서를 고려해 나열할 경우의 수
  * 순열과 조합의 차이는 순서의 고려 유무임

◾ 순열과 조합의 핵심 이론

🔸 순열

• 5개 중 2개를 순서대로 선택하는 경우의 수를 구하는 경우
  1번째 선택은 5개 데이터를 선택 가능하므로 5가지 선택 가능
  2번째 선택은 1번째에서 선택한 데이터를 제외한 4가지를 선택 가능
  따라서 5개 중 2개를 고르는 경우의 수는 5*4 = 20 가지가 됨

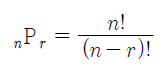
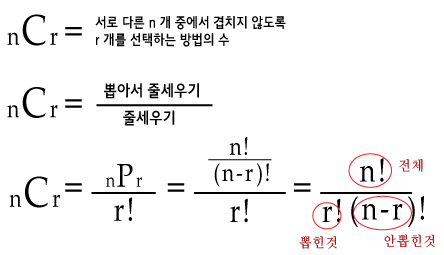
🔸 조합

• r! 은 순서가 다른 경우를 제거하는 역할을 함
• 5개 중 2개를 순서대로 선택하는 경우의 수를 구하는 경우
  1번째 선택은 5개 데이터를 선택 가능하므로 5가지 선택 가능
  2번째 선택은 1번째에서 선택한 데이터를 제외한 4가지를 선택 가능
  따라서 5개 중 2개를 고르는 경우의 수는 5*4 = 20 가지가 되고 거기서 나누기 2!를 하면 (2x1 = 2) 10이 나옴.

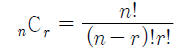
출처 : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=vollollov&logNo=220915481071

◾ 알고리즘 핵심사항

1. 특정 문제를 가정하기

ex) 5개의 데이터에서 3개를 선택하는 조합의 경우의 수

2. 모든 부분 문제가 해결 된 상황이라고 가정하고 지금 문제 생각하기

• 먼저 데이터 중 4개를 이미 선택 완료된 데이터라고 가정한 뒤, 마지막 데이터의 선택 여부에 따른 경우의 수를 계산
  만약, 데이터를 포함해 총 3개의 데이터를 선택하려면 선택이 완료됐다고 가정한 4개의 데이터에서 2개를 선택해야함.
  마지막 데이터를 포함하지않고 총 3개의 데이터를 선택하려면 이전 데이터 4개 중 3개를 선택해야 함.
  2가지 경우의 수를 합치면 5개 중 3개를 선택하는 경우의 수가 나옴

  

5개 중 3개를 선택하는 경우의 점화식
D[5][3] = D[4][2] + D[4][3]

3. 특정 문제를 해결한 내용을 바탕으로 일반 점화식 도출하기

조합 점화식
D[i][j] = D[i-1][j] + D[i-1][j-1]