@Algorithms
Copyrigh 2006 S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani July 18, 2006
3단원

---

1. Why Graphs?

Graph는 node라고도 불리는 점들의 집합과 두 점들 사이의 선들로 특정할 수 있다.
예를들어, $V = {1,2,3,...,13}$ and $E$ includes, among many other edges, $\{1, 2\}, \{9, 11\}$, and $\{7, 13\}$.
여기서 $\{7,13\}$이면 7과 13은 연결되어있다는 것인데, 이게 symmetric reaction이 되면 undirected graph라고 한다. 쉽게 말하면 7과 13의 관계가 7의 입장에서 봤을 때와 13의 입장에서 봤을 때가 같으면 undirected graph라는 것이다.

종종 graphs가 이러한 상호 관계가 없을 때도 있는데, 그렇다면 선을 그릴 때 방향도 그려줘야 한다. 그런 상황에서 $x$에서 $y$로 가는 edge를 표현할 때 $e=(x,y)$ 써주고, $y$에서 $x$로 가는 edge를 표현할 때 $(y,x)$ 라고 표현해준다.

1-1) How is a graph represented?

Graph는 adjacency matrix로 표현될 수 있다.
Adjacency matrix란? n개의 점들이 있다면 $(i,j)\text{th}$ entry가 아래와 같은 $n \times n$ 배열이다.
$a_{ij}=\begin{cases}1\quad\quad\text{if there is an edge from }v_i \text{ to } v_j\\0\quad\quad\text{otherwise}\end{cases}$

만약 undirected graph라면, matrix는 symmetric할 것이다.

이러한 형태의 가장 큰 편리점은 constant한 시간에 특정 edge의 존재를 확인할 수 있다는 점이다. 하지만 $O(n^2)$의 공간을 갖기 때문에, graph가 edges가 적다면 이는 낭비일 것이다.

다른의 표현법은 edge에 비례하는 크기를 갖는 "adjacency list"이다. 이것은 점마다 $|V|$ linked list로 구성되어 있다. 점 $u$의 linked list는 $u$에서 $v$로 가는 edge가 있다면 점 $v$가 $u$의 linked list에 저장되어 있다.

만약 directed graph라면 edge는 하나의 linked list에서 나타나고, undirected graph라면 edge는 두 개의 linked list에서 나타난다.

이럴 때 총 데이터 구조의 크기는 $O(|E|)$이다. 하지만 특정 edge를 찾는 것에 걸리는 시간은 constant time이 아니다. 왜냐면 $(u,v)$를 찾을 때, $u$의 adjacency list를 찾아봐야하기 때문이다. 하지만 하나의 점에 대한 adjacency list만 찾아보면 되기에 graph 알고리즘에서 유용한 작동 방식이다.

2. Depth-first search in undirected graphs

2-1) Exploring mazes

깊이 우선 검색(Depth-first search)은 그래프에 대한 풍부한 정보를 드러내는 놀랍도록 다용도적인 선형 시간(linear - time) 절차이다.
이것이 강조하는 가장 기본적인 질문은 "주어진 점들로부터 graph의 어떤 부분이 도달할 수 있는지"이다.

"도달(reachability)"는 미로를 탐험하는 것과 같다.
고정된 지점에서 걷기를 출발하고 니가 어느 교차점(vertex)에 도착할 때마다 따라갈 수 있는 다양한 통로(edges)가 있다.
부주의한 통로 선택은 너를 원을 돌게 만들 수 있거나 미로의 갈 수 있는 부분을 간과하게 할 수 있다. 그래서 탐험 중 중간 정보를 기록해야 한다.

미로를 탐험하는 데 필요한 것은 줄과 분필뿐이라는 것을 사람들은 알고 있다. 분필은 이미 지나간 교차로를 표시하여 무한 반복을 방지하고, 줄은 시작 장소로 되돌려주므로 이전에 보았지만 아직 조사하지 않은 통로로 다시 들어갈 수 있게 해준다.

컴퓨터에서 기본적인 요소인 분필과 줄을 어떻게 시뮬레이션할 수 있을까?

분필은 방문했는지를 체크하 수 있는 Boolean 변수를 이용하면 되고, 실은 stack을 이용하면 된다. 실의 정확한 역할에는 두 개의 operations가 있는데, 새로운 교차점에 들어가기 위해 스택에 넣는 것과 이전 교차로로 돌아가기 위해 스택에서 pop하는 것이다. stack을 명시적으로 유지하는 대신 재귀를 통해 암묵적으로 스택을 유지할 것이다.(이는 활성화 record의 스택을 사용하여 구현됨)

(밑의 그림 참고)
A node에서부터 시작한다고 하면, A-B edge와 B-E edge와 같이 아직 탐색되지 않은 점들을 이어주는 edge를 Tree Edges 라고 한다. 그리고 C-A 와 같이 점선으로 나타내진, 이미 탐색된 점으로 이어지는 Edge는 Back Edges라고 한다. (이게 이어지면서 Cycle을 만들어 냄.)

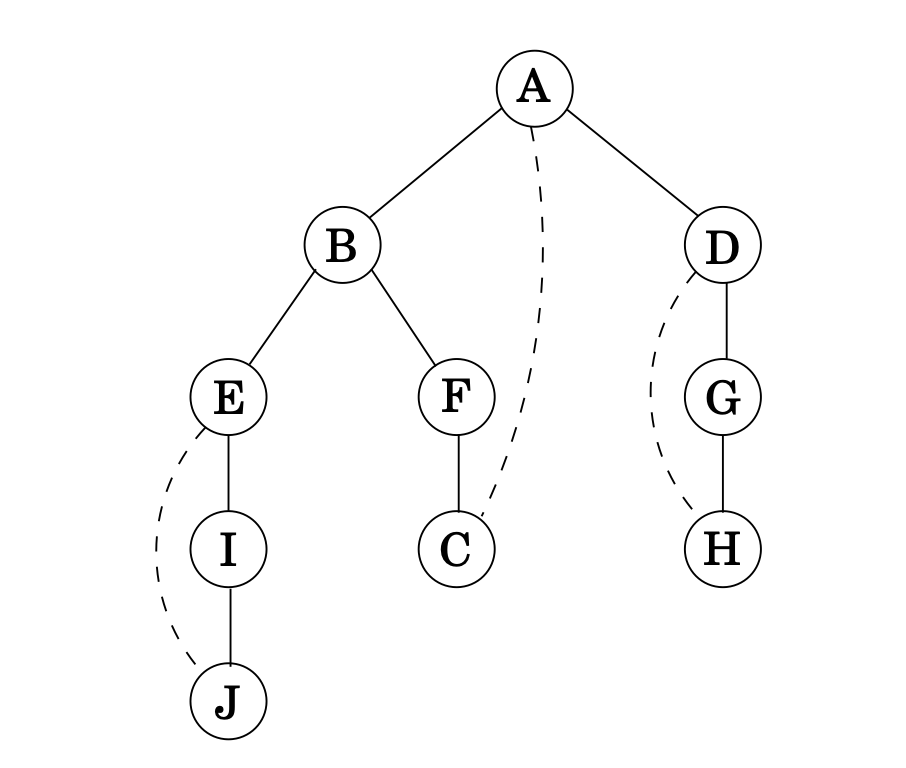
2-2) Depth-first search

탐험 절차는 그래프에서 시작점으로부터 닿을 수 있는 부분만 방문한다. 그래서 그래프에서 남은 부분을 검사하려면, 아직 방문되지 않은 다른 점에서부터 다시 절차를 시작해야한다.
그래서 모든 점들이 visited될 때까지 반복하는 알고리즘이 Depth-first search(DFS)다.

DFS의 running time을 확인하는 첫 번째 단계는 'visited array'를 이용하여 각 점들이 한 번 방문되었는지 확인하는 것이다. 점들을 탐험하면서 하는 것들은

1. 해당 점을 visited, pre/postvisit로 체크하는 작업 => 일정량 (Some fixed amount of work)
2. 인접한 edge가 새로운 곳으로 이어지는지 확인하기 위해 스캔되는 Loop

Loop는 각 점마다 다른 시간이 걸릴 것이기에, 모든 점들이 같이 있는 것을 생각해보자. 만약에 점들이 모두 이어져 있다면 step1에 모든 작업이 $O(|V|)$로 끝날 것이다.

Step2에서 총 DFS에서 Edge $\{x,y\} \in E$는 $x$를 탐험할 때 한 번, $y$를 탐험할 때 한 번, 총 2번 검사될 것이다.

step2의 총 시간은 그래서 $O(|E|)$이고, DFS의 running time은 $O(|V| + |E|)$이고, 입력 크기에 선형이다.

2-3) Connectivity in undirected graphs

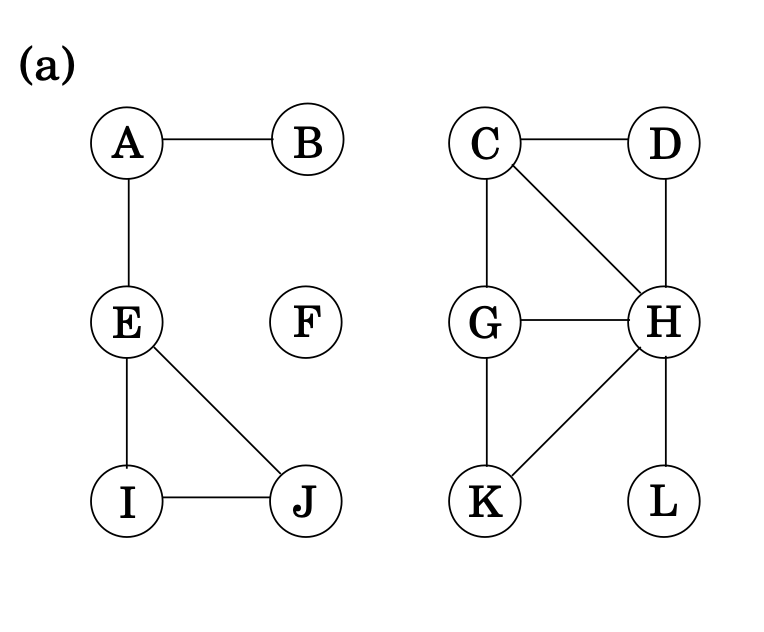
이 사진을 보면, Grpah가 connected 되었다고 볼 수 없는데 그 이유는 A에서 K로 가는 edge가 없기 때문이다.
하지만 3개의 disjoint connected regions가 있다.
바로 {A,B,E,I,J}, {C,D,G,H,K,L}, {F}. 이 3개의 regions를 connected components라고 부른다. 각자는 연결이 되어있지만, 서로에게 연결이 안되어있는 원래 Graph의 subgraphs.
Explore가 시작되면, 그 점이 어떤 connected components에 포함되어 있는지 확인할 수 있다.

깊이 우선 탐색(DFS)은 그래프가 연결되어 있는지 확인하고, 각각의 node에게 특정 integer를 부여하여 어떤 connect components에 속해있는지 알게 한다.

2-4) Previsit and postvisit orderings

Previsit와 postvisit을 시간을 적어놓는 작업.

순서

1. 탐색을 시작하기 전에 previsit 시간을 1로 초기화합니다.
2. 현재 노드를 previsit 시간으로 마킹하고, 해당 노드의 모든 이웃 노드를 탐색합니다. 이 과정에서 각 이웃 노드를 재귀적으로 방문하면서 previsit 및 postvisit 시간을 매깁니다.
3. 모든 이웃 노드를 방문한 후에 현재 노드의 postvisit 시간을 갱신합니다.

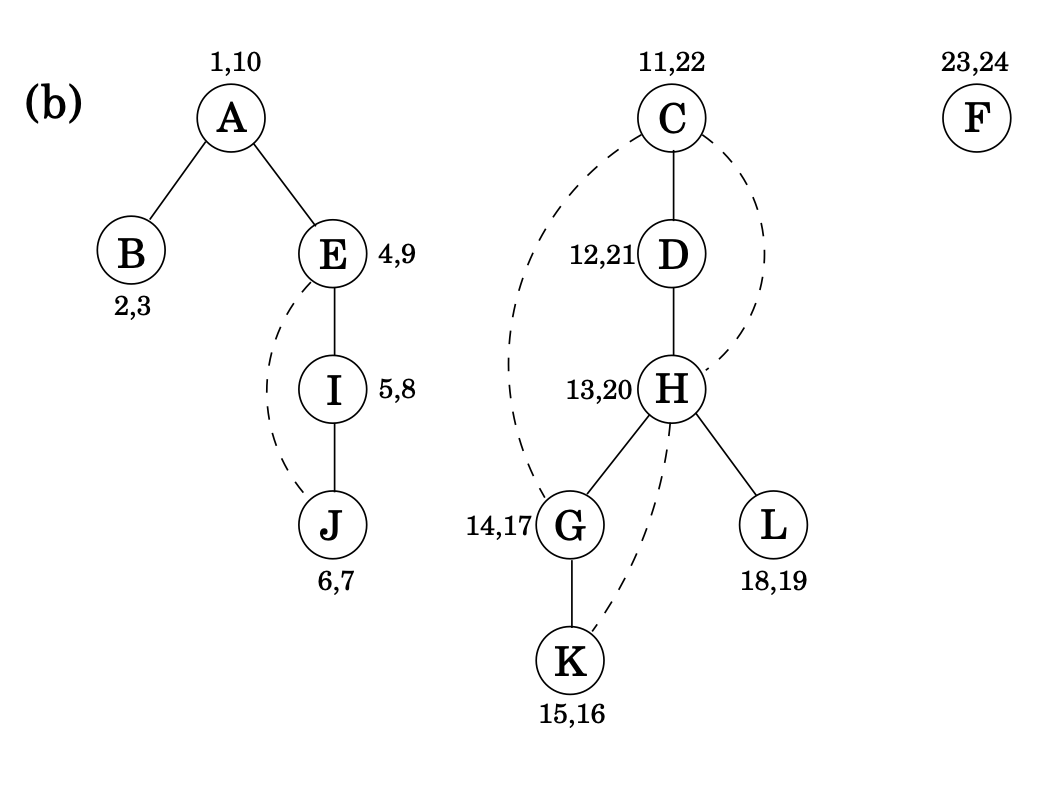
Property

For any nodes $u$ and $v$, the two intervals $[\text{pre}(u), \text{post}(u)]$ and $[\text{pre}(v), \text{post}(v)]$ are either disjoint or one is contained within the other.

즉, {A,B,E,I,J}를 보면 A가 시작과 끝을 담당하니까 B의 interval이 A의 interval에 들어가 있지만
D의 interval은 A와 완전히 disjoint한다!
결국 하나의 interval안에 감싸져 있거나(포함되어 있거나) 아니면 아예 겹치는 부분이 없다.

3. Depth-first search in directed graphs

3-1) Types of edges

Directed graphs는 두 점들의 관계에 대한 용어가 중요하다.
Ancestor, Descendant, parent, child 등..
$A \to B$인 edge가 있으면, A는 parent이고 B는 child이다.
여기서 $A \to B \to D$이면 $A$는 ancestor이고 $D$는 descendant 다.
큰 의미인데, parent이면 ancestor이다. (부모님도 조상님이니까) 반대도 같다. 즉, child이면 descendant다.

Tree edge와 non-tree edge만을 구분하는 undirected tree와 달리 directed tree는 조금 더 정교한 분류가 있다.

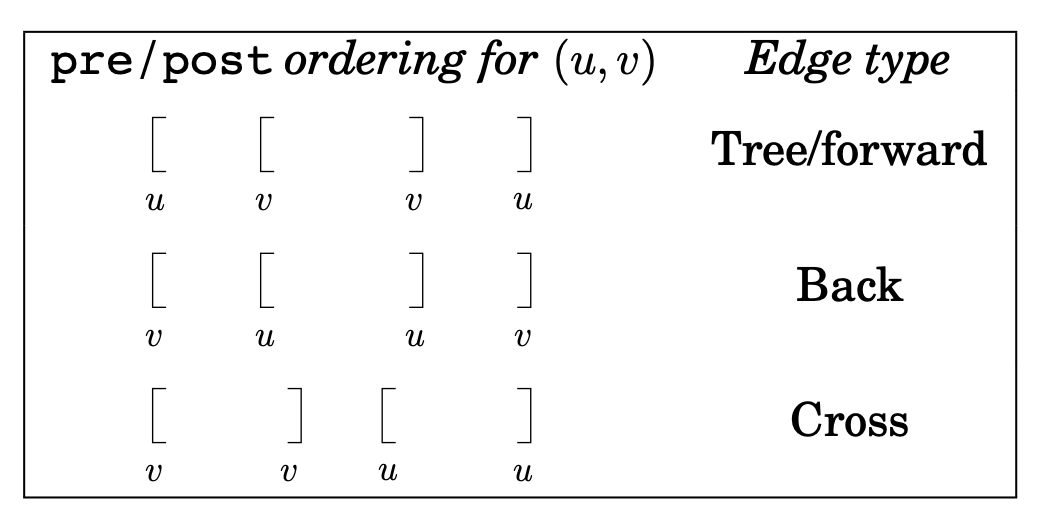
Ancestor과 descendant의 관계를 통해 edge type뿐만 아니라 pre/post numbers를 읽어낼 수 있다. 탐험 전략 때문에, $u$가 $v$의 ancestor이면 $u$가 먼저 발견되고, $u$를 탐험하는 중에 $v$를 발견한다.
This is to say $\text{pre}(u) < \text{pre}(v) < \text{post}(v) < \text{post}(u).$

Edge 카테고리는 ancestor-descendant 관계에 의한 것이기 때문에 pre-post numbers로부터 알 수 있다.

3-2) Directed acyclic graphs

Cycle이 없는 graph는 acyclic 이라고 한다.

Property

A directed graph has a cycle if and only if its depth-first search reveals a back edge.

$Proof)$ One direction is quite easy: if (u, v) is a back edge, then there is a cycle consisting of this edge together with the path from v to u in the search tree.

반대로, graph가 $v_0 \to v_1 \to \cdots \to v_k \to v_0$인 cycle이 있다면 이 cycle에서 가장 먼저 발견된 node를 확인해봐라(가장 먼저라는 것은 pre number 가 가장 낮은 node). 만약 이게 $v_i$ node이면 cycle 안의 다른 모든 $v_j$ nodes는 $v_i$로부터 닿을 수 있을 것이고 search tree 안에서 $v_i$의 descendants 일 것이다. 특히 $v_{i-1} \to v_i$의 edge(또는 $i=0$ 인 경우, $v_k \to v_0$)는 해당 노드에서 ancestor로 연결되는 역할을 하며, 정의에 따라 back edge다.

줄여서 dag라고 불리는 directed acyclic graphs(비순환적 방향성이 있는 graph)는 항상 나타난다. 이는 인과관계, 계층 구조, 시간적 의존적인 관계를 표현하는데 좋다.

선행관계가 필요한 것들을 ordering 하는 것을 생각해보자. 만약에 여기서 cycle이 있으면 안된다 (순환이 계속 도니까 먼저 해야할 일을 찾을 수가 없다). 그러나 dag이면, 그래프를 선형화하고(위상 정렬하고), 우선 순위에 맞춰 배열할 수 있다.

어떤 type의 dag가 선형화 될 수 있을까? 정답은 모두 다!(All of them)
어떻게 할까? post numbers의 내림차순으로 수행하면 된다.

Dag는 back-edge를 가지면 안된다! 따라서,

Property

In a dag, every edge leads to a vertex with a lower post number.

이는 dag의 점들을 linear-time에 ordering하는 algorithms을 준다. 그리고 전의 발견된 것들을 보면 달라보이는 서로 다른 성질 'acyclicity', 'linearizability', 'DFS에서 back-edges의 부재'가 사실은 하나였다는 것을 알 수 있다.

Dag는 post numbers의 내림차순으로 선형화되니까, 선형화에서 가장 마지막에 오는 것이 가장 작은 post number를 가지는 점이어야한다(It must be a sink - no outgoing edges, 그 점은 밖으로 나가는 선이 없는 'sink'여야 한다). 비슷하게 가장 높은 post number를 갖는 점은 다른 점으로부터 들어오는 edge가 없는 점이어야 한다(Source : a node with no incoming edges).

Property)

Every dag has at least one source and at least one sink.

Source : incoming edge가 없는 node
Sink : outgoing edge가 없는 node

4. Strongly connected components

4-1) Defining connectivity for directed graphs

Undirected graph에서의 connectivity는 간단하다: 연결되어 있지 않은 graph는 connected components로 분해될 수 있다.

Directed graph에서 connectivity는 더 미묘하다.
Directed graph에서 connectivity를 정의하는 옳바른 방법은 아래이다.

Connectivity in directed graph

Two nodes $u$ and $v$ of a directed graph are connected if there is a path from $u$ to $v$ and a path from $v$ to $u$.

This relation partitions $V$ into disjoint sets (Exercise 3.30) that we call strongly connected components. The graph of Figure 3.9(a) has five of them.

이러한 관계는 전체를 "strongly connected components"라고 불리는 disjoint set으로 나눈다. 밑의 그림은 5개의 strongly connected components로 이루어져 있다.

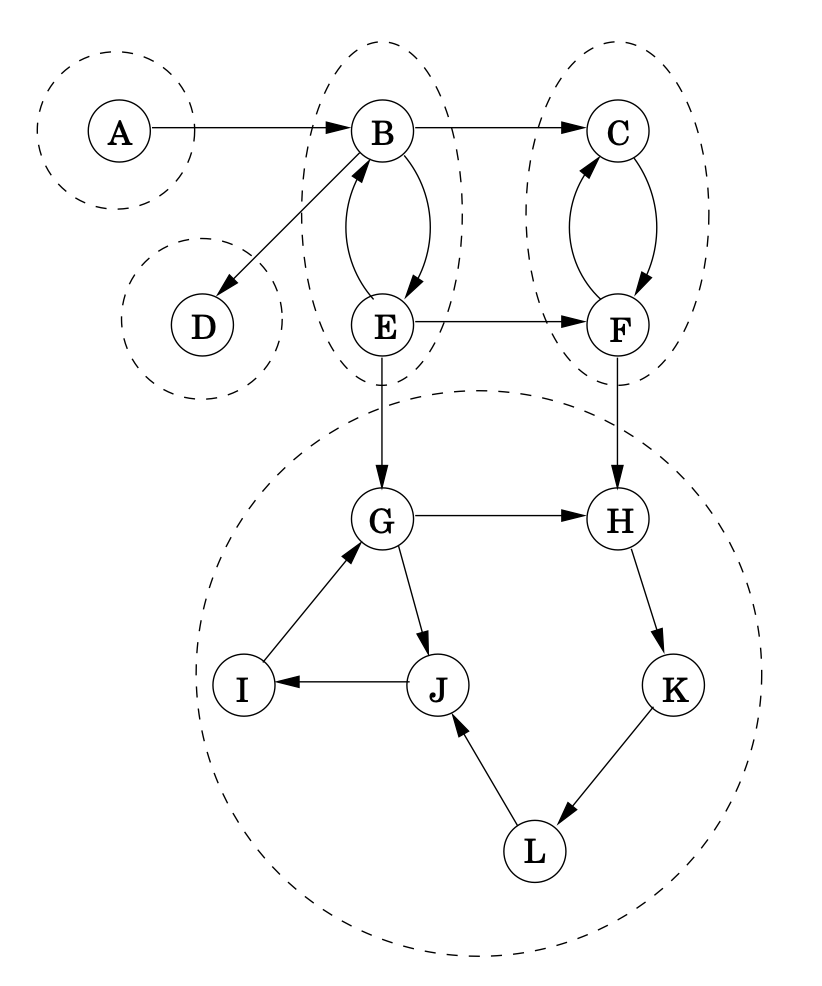
Strongly connected components를 하나의 meta-node로 두고, meta-node끼리 이어지는 edge가 있으면 이를 이어주는 edge도 그려보자.

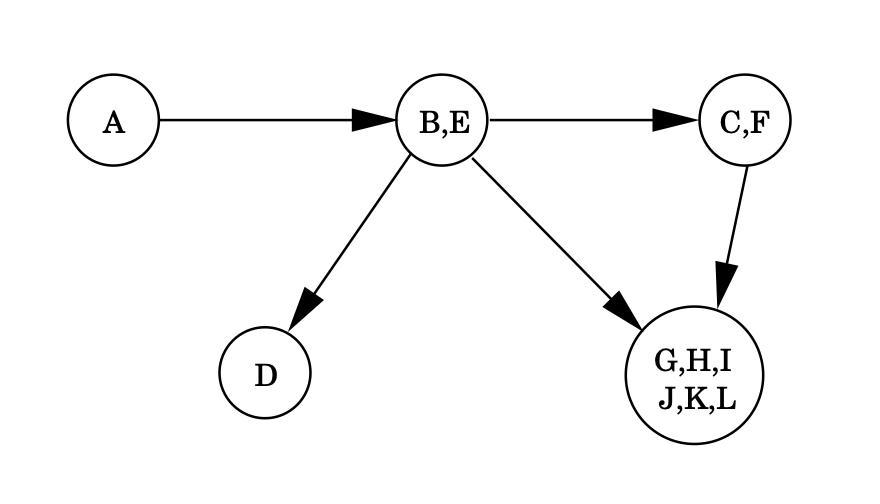
이러한 meta-graph의 결과는 항상 dag다.

Property

Every directed graph is a dag of its strongly connected components.

이를 통해서 알 수 있는 것: Directed Graphs의 connectivity structure은 2개의 층으로 이루어져 있다.
가장 상위에는 간단한 구조인 dag를 갖고 있고, 더 디테일을 보고 싶으면 dag의 한 점을 보면된다. 그러면 완전한 strongly connected components를 볼 수 있다.

4-2) An efficient algorithm

Directed graphs를 strongly connected components로 분해하는 것은 매우 유용하다. 이미 본 성질들을 더 자세히 보며, 깊이 우선 탐색을 더욱 활용하여 이를 선형 시간 안에 찾을 수 있는 알고리즘이 있다.

Property 1

If the explore subroutine is started at node u, then it will terminate precisely when all nodes reachable from u have been visited.

그래서 만약 meta-graph에서 sink node 안의 한 점의 explore를 부를 수 있으면, 우리는 정확히 그 component를 회수할 수 있다.

이는 strongly connected component를 찾는 하나의 방법을 제시하지만 아직 두 개의 문제가 남아있다:
(A): 어떻게 확실히 sink인 strongly connected component의 한 점을 뽑을 수 있을까?
(B): 이 첫 번째 구성 요소가 발견되면 어떻게 계속해야 할까?

(A)에 대해 먼저 이야기해보면, 'Source'인 strongly connected component 안의 하나의 점을 뽑는 방법이 있다.

Property 2

The node that receives the highest post number in a depth-first search must lie in a source strongly connected component.

This follows from the following more general property.

Property 3

If $C$ and $C'$ are strongly connected components, and there is an edge from a node in $C$ to a node in $C'$, then the highest post number in $C$ is bigger than the highest post number in $C'$.

Property 3은 strongly connected components가 그들의 highest post numbers를 내림차순으로 배열함으로써 linearized 할 수 있는 것이라고 다시 말할 수 있다.

Property 2는 $G$에서 source인 strongly connected component 안의 한 점을 찾을 수 있게 도와준다. 하지만 우리는 sink component의 한 점을 찾아야하는 우리의 필요와 반대인 것처럼 보인다.

$G$와 같지만 edge의 방향만 반대인 reverse graph $G^R$를 생각해보자. $G^R$은 $G$와 정확히 같은 strongly connected components를 가진다.
그렇다면 여기서 $G^R$의 source인 strongly connected component를 찾으면 이는 $G$에서 sink인 strongly connected component일 것이다.
$\Rightarrow$ (A)는 해결!

그럼 다음 문제인 (B). 첫 sink component를 찾은 후에는 어떻게 해야하는가? 답은 Property 3을 통해 알 수 있다.
Sink component를 graph에서 지운다면, highest post number를 이용하여 남은 점들 중에 sink component를 알 수 있을 것이다.

Resulting Algorithms은

1. Depth-first search on $G^R$.
2. Run the undirected connected components algorithm (from Section 2-3) on $G$, and during the depth-first search, process the vertices in decreasing order of their post numbers from step 1.

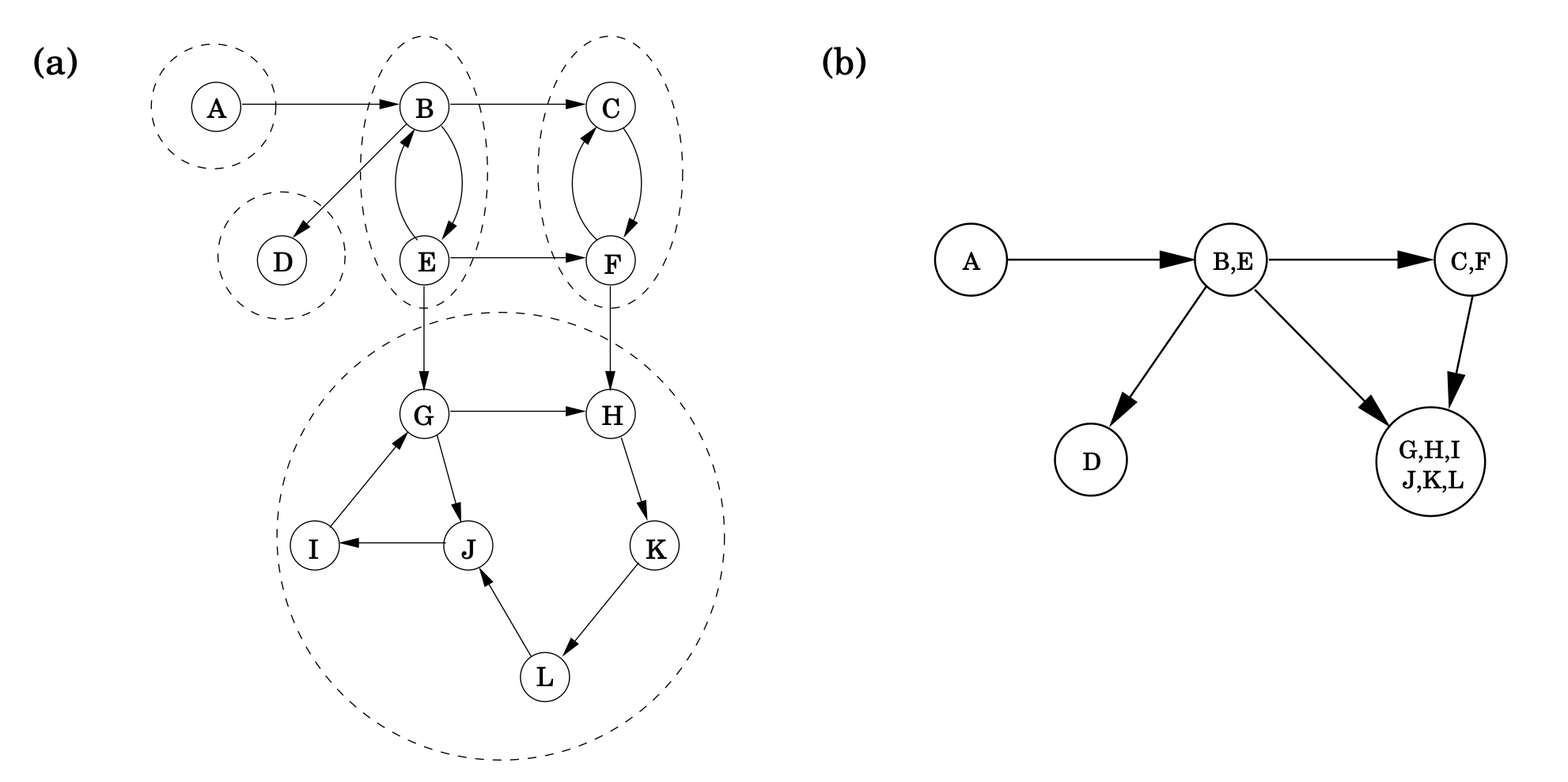
알고리즘을 위의 graph에서 돌려보자.
만약 step 1이 점들을 사전 순서를 고려한다면, 두 번째 단계에대해 설정한 순서는 다음과 같습니다(즉, $G^R$의 DFS 에서의 post numbers의 내림차순): $G, I, J, L, K, H, D, C, F, B, E, A$

Then step 2 peels off components in the following sequence: {G, H, I, J, K, L}, {D}, {C, F }, {B, E}, {A}.